Principali costruzioni geometriche delle coniche e loro equazioni rappresentative
Nelle pagine che da questa hanno origine presentiamo le principali costruzioni geometriche delle coniche appoggiandoci ad un software di geometria dinamica qual è GeoGebra. Ciascuna costruzione fa uso dei tradizionali strumenti della geometria euclidea cioè della riga e del compasso o di loro combinazioni e, tramite la loro controparte software, si giunge a definire un punto appartenente alla conica o, nel caso dell'ultima costruzione di ciascuna conica, la retta tangente. L'animazione di questo punto o della retta tangente permette poi di riconoscere la curva studiata come luogo di punti che soddisfano ad opportune condizioni.
Prendendo lo spunto dalla costruzione geometrica che, di norma, riprende la definizione più diffusa, e con l'introduzione di un sistema cartesiano deduciamo quindi l'equazione canonica della conica o una coppia di sue equazioni parametriche dalle quali derivare, eventualmente, la forma canonica.
L'ultima costruzione di ciascuna conica sfrutta infine la nozione di curva inviluppo, definizione che viene gradualmente sviluppata nella pagina riguardante la parabola e dove si giunge ad una sua formalizzazione utilizzando conoscenze di Analisi quali i concetti di limite e di derivata. Questa pagina è quindi propedeutica a quelle finali dell'ellisse e dell'iperbole e va intesa come un ulteriore approfondimento per coloro che già conoscono, appunto, il calcolo dei limiti e la nozione di derivata.
Ciascuno dei link sottostanti punta ad una pagina dove appare inizialmente l'esito finale della costruzione e, poiché le pagine possono essere consultate per gran parte indipendentemente una dall'altra, termina con un ritorno a questa pagina piuttosto che con un rimando alla successiva.
Parabola
- Nella prima costruzione si fissano la direttrice ed il fuoco F e si costruisce la parabola come luogo di punti aventi la medesima distanza da questi due elementi geometrici.
- Nella seconda costruzione si fissano il vertice V ed un secondo punto appartenente all'asse della parabola.
- La terza costruzione parte dal disporre della direttrice e del fuoco.
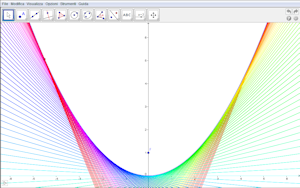
- Nella quarta costruzione si ottiene la parabola come inviluppo delle sue rette tangenti.
Ellisse

- Nella prima costruzione vengono fissati i due fuochi e la somma delle distanze del punto dell'ellisse dai fuochi.
- La seconda costruzione è una generalizzazione della precedente. Pure qui vengono fissati i due fuochi e la somma delle distanze del punto dell'ellisse dai fuochi.
- Nella terza costruzione si ottiene l'ellisse a partire dalle lunghezze dei due suoi semiassi definite tramite i raggi di due circonferenze. Si deduce quindi l'equazione canonica e la sua più nota rappresentazione parametrica.
- Nella quarta costruzione si assegnano i vertici dell'asse maggiore e la distanza focale e i punti dell'ellisse emergono come intersezioni di due opportune famiglie di circonferenze. A partire da queste ultime si deduce poi l'equazione canonica.
- La quinta costruzione fissa la somma dei due semiassi e il valore di uno di essi (compasso ellittico). Alcune osservazioni finali forniscono lo spunto per lo studio di altre curve.
- In questa sesta costruzione l'ellisse emerge come inviluppo delle sue rette tangenti. Attraverso la costruzione della famiglia di tangenti si giunge ad una prima parametrizzazione dalla quale discende l'equazione canonica. Si fornisce quindi un'ulteriore e più generale parametrizzazione di tale curva.
Iperbole
- Nella prima costruzione fissati i due fuochi si ottiene l'iperbole come luogo di punti per i quali è costante la differenza delle distanze da tali punti fissi.
- Nella seconda costruzione si generalizza la precedente costruzione partendo ancora dalla medesima definizione.
- Nella terza costruzione si definiscono in partenza fuochi e vertici e, in analogia a quanto fatto per l'ellisse, si individuano i punti dell'iperbole come intersezioni di due famiglie di circonferenze. Lo studio analitico conduce ad una rappresentazione parametrica dalla quale otteniamo l'equazione canonica. Si mostra infine come le linee di interferenza costruttiva (o distruttiva) di due sorgenti in fase costituiscano una famiglia discreta di iperboli.
- Nella quarta costruzione si deduce l'iperbole assegnate le lunghezze dei due semiassi da cui discende facilmente l'equazione canonica e, con un opportuno parametro angolare, una sua rappresentazione parametrica.
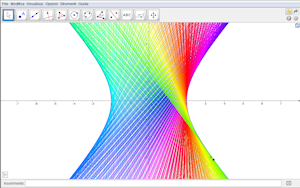
- Infine, come nei casi precedenti, la costruzione proposta conduce ad individuare una generica retta tangente in modo che l'iperbole appaia come l'inviluppo della famiglia di tali rette. La descrizione della famiglia in termini di un parametro permette di giungere ad una rappresentazione parametrica dalla quale dedurre l'equazione canonica.