Ellisse: costruzione n. 6
Quale ultima costruzione intendiamo ottenere l'ellisse come inviluppo delle sue rette tangenti. Se nel caso della parabola le rette tangenti passavano tutte per un punto variabile su una retta, qui il punto si muove lungo una circonferenza.
- Tracciamo quindi la retta asse x scrivendo \(y=0\) nella barra di inserimento (fig. 2.17).
- Va costruita ora la circonferenza c di centro l'origine A e raggio AB, per esempio definendo B come \(B(5,0)\). La lunghezza del raggio di tale circonferenza è pari alla lunghezza del semiasse maggiore dell'ellisse.
- Per definire la posizione dei fuochi sull'asse, tracciamo la circonferenza di centro A e raggio \(AC<AB\), per esempio scegliendo C come \(C(3,0)\).
- Sia E l'ulteriore punto di intersezione tra l'asse x e quest'ultima circonferenza (che, per chiarezza, successivamente nascondiamo).
- Definito uno slider \(\alpha\) angolare, selezioniamo lo strumento angolo di data misura
 e quindi
e quindi
- definiamo l'angolo BAG avente misura pari ad \(\alpha\) con G punto sulla circonferenza iniziale c.
- Disegniamo ora la retta EG e quindi
- la retta perpendicolare a questa passante per G. È quest'ultima che risulta essere tangente all'ellisse.
Al variare quindi del punto G cioè, algebricamente, dell'angolo \(\alpha\) che lo descrive, disponiamo ora di una famiglia di rette dove ciascuna retta ha la proprietà di essere tangente ad una curva che appare essere un'ellisse. La curva che in tal modo emerge costituisce, come sappiamo, l'inviluppo di tale famiglia.
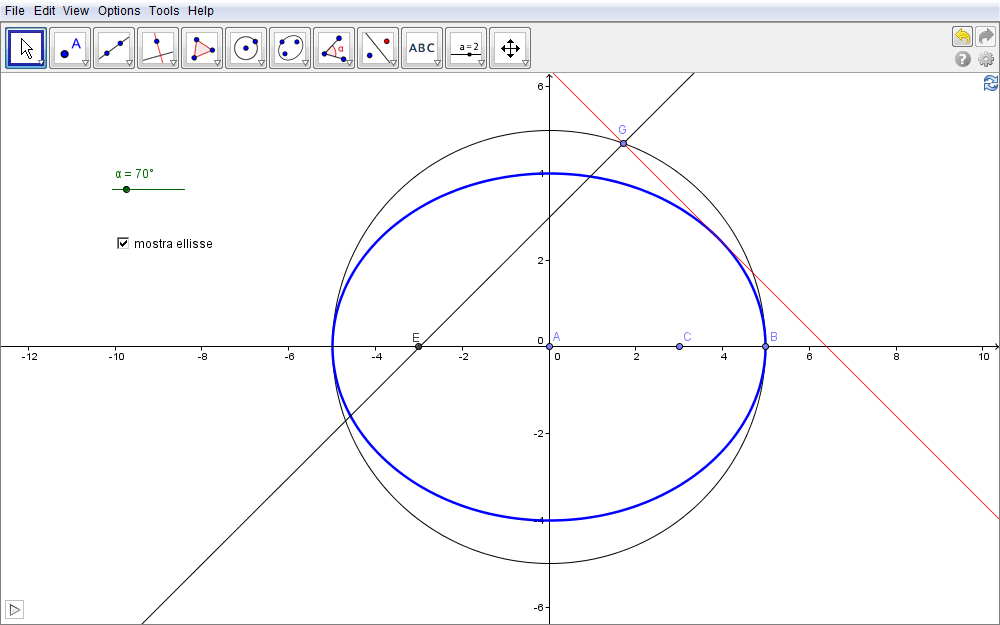
Difatti in fig. 2.17 è sufficiente attivare la traccia di tale retta (clic destro, Traccia attiva), e quindi avviare l'animazione dello slider (animazione attiva oppure clic sul pulsante in basso a sinistra) per far emergere l'ellisse come inviluppo delle sue rette tangenti. Per visualizzarla clic sulla casella di controllo mostra ellisse.
Figura 2.17. ellisse17.ggb.
Approfondimento. Equazione dell'inviluppo
Nel caso della parabola siamo stati in grado di ottenere, a partire dalla famiglia delle sue rette tangenti, la sua equazione rappresentativa dimostrando così come tale curva sia, per l'appunto, l'inviluppo della famiglia delle sue rette tangenti. Inizialmente la deduzione là presentata ha coinvolto nozioni elementari di geometria analitica ed è stata possibile in quanto il luogo dei punti G era la stessa retta direttrice e ciò ha permesso di determinare facilmente il punto di tangenza. Nel caso dell'ellisse il punto G varia invece su una circonferenza e non è immediato individuare il punto di tangenza con metodi algebrici.
Come spunto per eventuali approfondimenti (d'esame?) ci proponiamo quindi di applicare il metodo generale formalizzato di seguito nella quarta pagina riguardante la parabola e che permette di ottenere, con la risoluzione di un sistema di equazioni, la rappresentazione della curva inviluppo di una famiglia di curve dipendente da un parametro. Come visto, la sola nozione accessoria richiesta è il calcolo di una derivata.
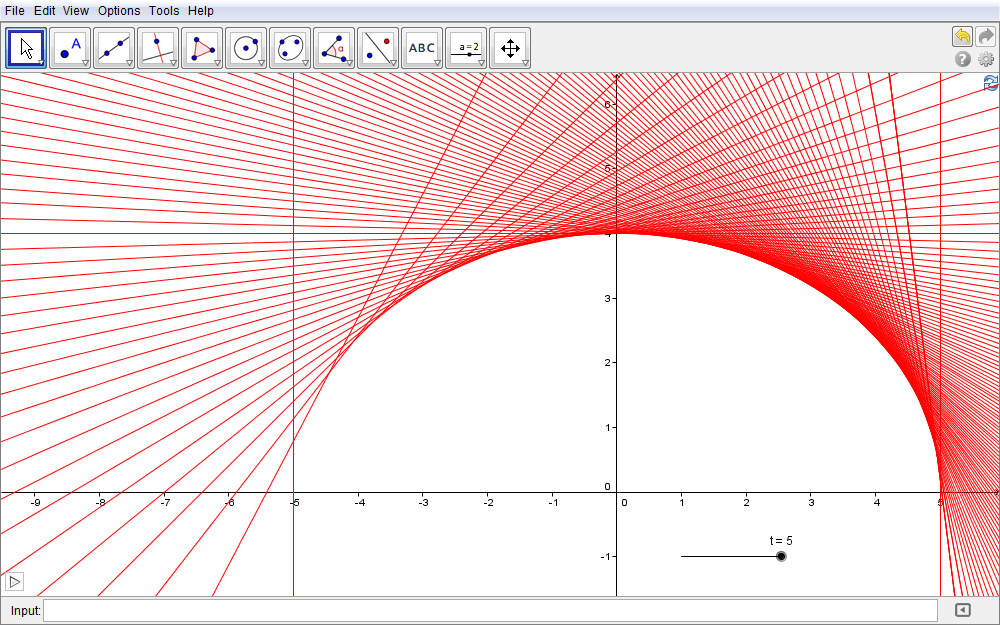
In riferimento alla figura precedente supponiamo che le coordinate del punto E siano \(E(-c,0)\) con \(c>0\) (in figura \(c=3\)). Se scegliamo come parametro l'ascissa di G ossia poniamo \(x_G=t\), la sua ordinata discende dall'appartenenza di G alla circonferenza con raggio \(AB=a\) (in figura \(a=5\)) e quindi risulta \begin{equation}t^2+y^2=a^2\quad\Rightarrow\quad y=\pm\sqrt{a^2-t^2},\end{equation} e, per la simmetria della costruzione, possiamo limitarci a considerare nel seguito \begin{equation}y_G=\sqrt{a^2-t^2}.\end{equation} Il coefficiente angolare della retta EG è \begin{equation}m_{EG}={y_G-y_E\over x_G-x_E}={\sqrt{a^2-t^2}\over t+c}\end{equation} per cui la famiglia di rette tangenti all'ellisse passanti per G e perpendicolari ad EG possiede equazione \begin{equation}y-y_G=-{1\over m_{EG}}(x-x_G)\quad\Rightarrow\quad y-\sqrt{a^2-t^2}=-{t+c\over\sqrt{a^2-t^2}}(x-t)\end{equation} che, per evitare singolarità al denominatore, riscriviamo come \begin{equation}y\sqrt{a^2-t^2}-(a^2-t^2)=-(t+c)(x-t),\end{equation} oppure trasportando tutti i termini a primo membro e riducendo i termini simili nella forma implicita \begin{equation}y\sqrt{a^2-t^2}+t(x-c)+cx-a^2=0.\label{eq:6}\end{equation} Quest'ultimo risultato possiamo inserirlo in GeoGebra dopo aver comunque associato al parametro t uno slider che, per le scelte fatte (\(a=5\) e \(c=3\)), dovrà variare nell'intervallo \([-5, 5]\). Otteniamo in tal modo la figura
2.18 dove, attivando l'animazione appare la (semi)ellisse inviluppo.
Figura 2.18. ellisse18.ggb.
Osserviamo come a primo membro della \eqref{eq:6} compaiano le tre grandezze variabili x, y e t assieme ai parametri fissati a e c. Possiamo quindi riscrivere la famiglia in termini più generali definendo una funzione \(F\) tale che \begin{equation}F(x,y,t)=y\sqrt{a^2-t^2}+t(x-c)+cx-a^2=0\label{eq:sette}\end{equation} e riprendere quanto descritto per giungere all'inviluppo di una famiglia di curve \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{F(x,y,t)=0\cr\cr {{\rm d}F\over{\rm d}t}=0\cr}}\label{eq:8}\end{equation} e dove la seconda equazione esprime la derivata della \eqref{eq:sette} rispetto al solo parametro t.
Nel nostro caso risulta \begin{equation}{{\rm d}F\over{\rm d}t}={-yt\over\sqrt{a^2-t^2}}+x-c\end{equation} per cui dovremo risolvere il sistema \begin{equation}\cases{y\sqrt{a^2-t^2}+t(x-c)+cx-a^2=0\cr\cr {-yt\over\sqrt{a^2-t^2}}+x-c=0.\cr}\end{equation} Pertanto esplicitamo dalla seconda l'incognita \(y\) \begin{equation}y={(x-c)\sqrt{a^2-t^2}\over t}\label{eq:undici}\end{equation} e sostituendola nella prima abbiamo \begin{equation}{(a^2-t^2)(x-c)\over t}+tx-ct+cx-a^2=0.\end{equation} Moltiplicando per \(t\) e riducendo i termini simili si giunge alla \begin{equation}x(a^2+ct)=a^2c+a^2t\end{equation} da cui \begin{equation}x={a^2(c+t)\over a^2+ct}.\end{equation} Sostituiamo questo risultato nella \eqref{eq:undici} \begin{equation}y=\biggl({a^2c+a^2t\over a^2+ct}-c\biggr){\sqrt{a^2-t^2}\over t}\end{equation} e otteniamo \begin{equation}y={a^2-c^2\over a^2+ct}\sqrt{a^2-t^2}.\end{equation} In definitiva la coppia di equazioni \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{x={a^2(c+t)\over a^2+ct},\qquad y={a^2-c^2\over a^2+ct}\sqrt{a^2-t^2}}\label{eq:17}\end{equation} rappresentano la curva inviluppo che, nel nostro caso, è una (semi)ellisse. Per una conferma visiva potremmo inserire in GeoGebra tale coppia di equazioni tramite il comando curva[] ma, dato che ci aspettiamo una conica canonica, intendiamo ottenere la sua equazione implicita standard: dobbiamo a tal fine eliminare la dipendenza dal parametro t.
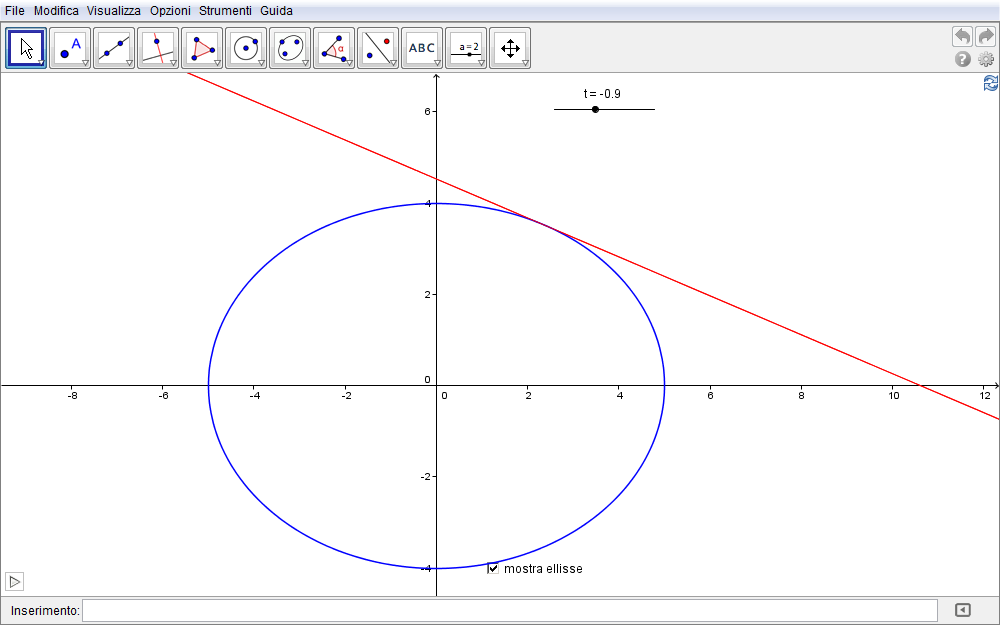
Anziché esplicitare t dalla prima delle \eqref{eq:17} e sostituirla nella seconda e, poiché sappiamo che l'equazione canonica di un'ellisse coinvolge i quadrati delle variabili, preferiamo seguire una via alternativa. Eleviamo pertanto al quadrato entrambe le equazioni \eqref{eq:17} moltiplicando la prima per \(a^2-c^2\) e la seconda per \(a^2\) (trascuriamo le ovvie condizioni di positività su x e y) \begin{equation}(a^2-c^2)\,x^2={a^4(c+t)^2(a^2-c^2)\over (a^2+ct)^2}\qquad a^2y^2={a^2(a^2-c^2)^2(a^2-t^2)\over (a^2+ct)^2}.\end{equation} Se ora sommiamo membro a membro e fattorizziamo i termini comuni a secondo, otteniamo \begin{equation}(a^2-c^2)\,x^2+a^2y^2={a^2(a^2-c^2)\over (a^2+ct)^2}\cdot\bigl[a^2(c+t)^2+(a^2-c^2)(a^2-t^2)\bigr]\end{equation} e sviluppando i quadrati entro le parentesi quadre si giunge alla \begin{equation}(a^2-c^2)\,x^2+a^2y^2={a^2(a^2-c^2)\over (a^2+ct)^2}\cdot\bigl[a^4+2a^2ct+c^2t^2\bigr]\end{equation} che si semplifica in \begin{equation}(a^2-c^2)\,x^2+a^2y^2=a^2(a^2-c^2).\end{equation} È sufficiente ora dividere per \(a^2(a^2-c^2)\) per giungere all'equazione canonica dell'ellisse \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{{x^2\over a^2}+{y^2\over a^2-c^2}=1}\end{equation} e che ci permette di confermare formalmente come il parametro \(a\) rappresenti la lunghezza del semiasse focale e \(c\) l'ascissa di un fuoco. Introdotta tale equazione in GeoGebra tramite la barra di inserimento si ottiene immediata conferma visiva della coincidenza della curva inviluppo con le rispettive rette tangenti (fig. 2.19).
Figura 2.19. ellisse19.ggb.
Approfondimento. Una parametrizzazione alternativa
La scelta del parametro t nella sezione precedente ci ha obbligati a trattare la sola semiellisse di ordinate positive onde mantenere la corrispondenza biunivoca tra t e il punto G sulla circonferenza. Qui intendiamo mostrare come, con una scelta diversa, si possa comunque ottenere il medesimo risultato per la curva inviluppo. A tale scopo non presenteremo i particolari di calcolo (sono riportati invece nel caso dell'iperbole) ma solo gli elementi principali della deduzione.
Figura 2.20. ellisse20.ggb.
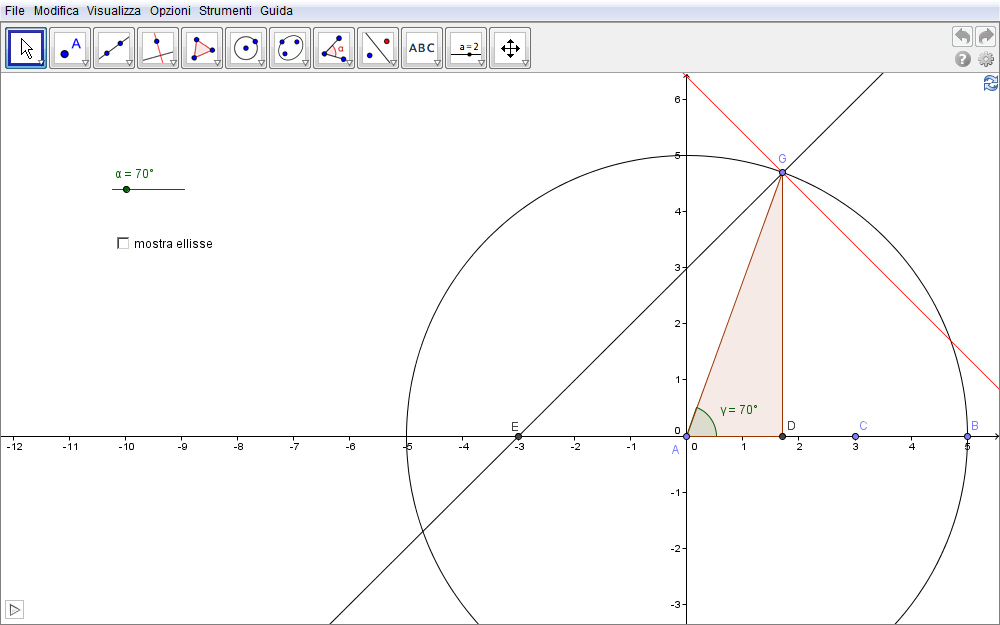
In riferimento alla fig. 2.20 scegliamo come parametro l'angolo \(\gamma=\angle BAG\) che è collegato, e numericamente uguale, allo slider \(\alpha\). Di conseguenza il punto \(G\) è individuato dalle coordinate \(G(a \cos\gamma, a\sin\gamma)\) dove \(a\) è ancora il raggio della circonferenza. Analogamente \(E(-c,0)\) per cui il coefficiente angolare di \(EG\) è ora \begin{equation}m_{EG}={y_G-y_E\over x_G-x_E}={a\sin\gamma\over a\cos\gamma+c}\end{equation} e l'equazione della famiglia di tangenti \begin{equation}y-y_G=-{1\over m_{EG}}(x-x_G)\quad\Rightarrow\quad y-a\sin\gamma=-{a\cos\gamma+c\over a\sin\gamma}(x-a\cos\gamma)\end{equation} che riportato, per convenienza, alla forma implicita è \begin{equation}a y\sin\gamma +a(x-c)\cos\gamma+cx-a^2=0.\label{eq:25}\end{equation} Il calcolo della derivata prima della funzione a primo membro eseguito rispetto alla variabile \(\gamma\) fornisce \begin{equation}ay\cos\gamma-a(x-c)\sin\gamma=0\end{equation} cosicché, in linea con le condizioni \eqref{eq:8}, va risolto il sistema \begin{equation}\cases{a y\sin\gamma +a(x-c)\cos\gamma+cx-a^2=0\cr ay\cos\gamma-a(x-c)\sin\gamma=0.\cr}\end{equation} Il risultato cui si giunge è \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{x={a(c+a\cos\gamma)\over a+c\cos\gamma}\qquad y={(a^2-c^2)\sin\gamma\over a+c\cos\gamma}}\label{eq:28}\end{equation} e rappresenta parametricamente il luogo inviluppo e, assieme, il punto di tangenza. Infine si deduce facilmente che tale coppia di equazioni soddisfa all'equazione canonica dell'ellisse \begin{equation}{x^2\over a^2}+{y^2\over a^2-c^2}=1\end{equation} già vista precedentemente. Nella figura 2.21 tutti gli elementi presenti sono stati introdotti a partire dalla barra di inserimento sfruttando le rappresentazioni parametriche date dalle \eqref{eq:25} e \eqref{eq:28}.
Figura 2.21. ellisse21.ggb.