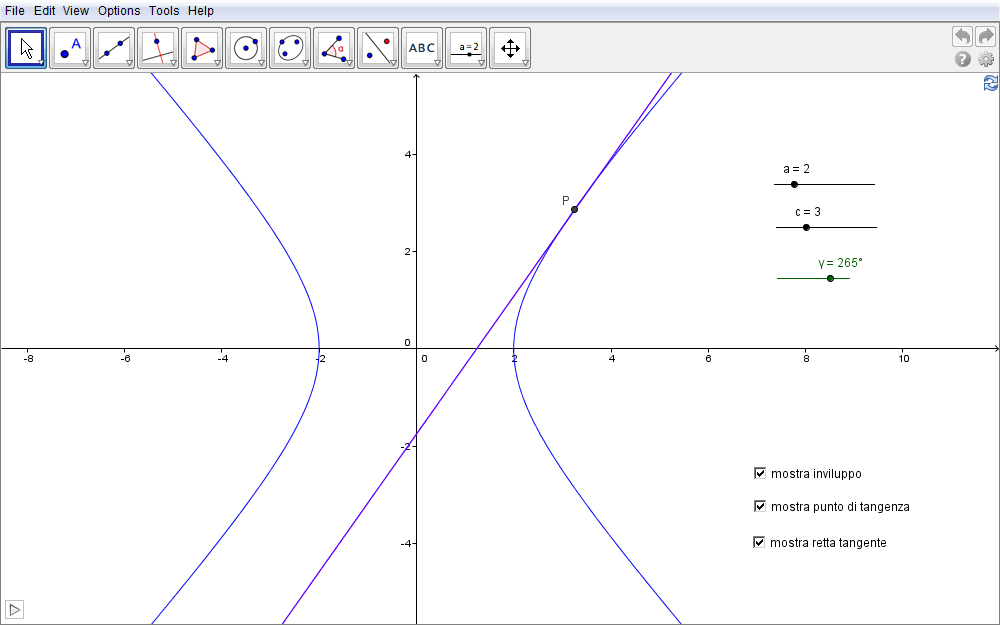
Iperbole: costruzione n. 5
In questa costruzione intendiamo ottenere l'iperbole come inviluppo delle sue rette tangenti per cui, come nel caso della parabola e dell'ellisse, lo scopo è di costruire essenzialmente la famiglia delle rette tangenti associando ciascuna retta di tale insieme ad un punto variabile. Riprodurremo quindi passo passo la medesima costruzione seguita per l'ellisse con l'unica variante nella posizione reciproca tra il punto e la circonferenza definiti inizialmente. Se quindi nel caso dell'ellisse la circonferenza aveva raggio maggiore della lunghezza del semiasse focale e di conseguenza i fuochi erano interni ad essa, in questa pagina avrà un raggio minore e i fuochi saranno ad essa esterni. Pertanto,
- tracciamo la retta asse x scrivendo \(y=0\) nella barra di inserimento e
- costruiamo la circonferenza c di centro l'origine A e raggio \(AB\) definendo B come \(B(4,0)\). La lunghezza del raggio di tale circonferenza rappresenta la lunghezza del semiasse trasverso (o focale) dell'iperbole.
- Per definire la posizione dei fuochi sull'asse, tracciamo la circonferenza di centro A e raggio \(AC>AB\), per esempio scegliendo in questo caso C come \(C(5,0)\). Si procede ora allo stesso modo che nel caso dell'ellisse.
- Sia E l'ulteriore punto di intersezione tra l'asse x e quest'ultima circonferenza (che, per chiarezza, abbiamo nascosto).
- Definito uno slider angolare \(\alpha\), selezioniamo lo strumento angolo di data misura
 e quindi
e quindi
- definiamo l'angolo BAG avente misura pari a \(\alpha\) con G punto sulla circonferenza c iniziale.
- Disegniamo ora la retta EG e quindi
- la retta perpendicolare a questa passante per G. È quest'ultima che risulta essere la tangente all'iperbole.
Al variare quindi del punto G cioè, algebricamente, dell'angolo \(\alpha\) che lo individua, disponiamo di una famiglia di rette dove ciascuna di queste ha la proprietà di essere tangente ad una iperbole che per questo motivo rappresenta l'inviluppo di tale famiglia. A conferma visiva e per far emergere l'iperbole, attivata nella fig. 3.14 la traccia per tale retta (clic destro, Traccia attiva), avviare l'animazione dello slider (animazione attiva oppure clic sul pulsante in basso a sinistra). Per visualizzarla clic sulla casella di controllo mostra ellisse.
Figura 3.14. iperbole14.ggb.
Approfondimento. Equazione dell'inviluppo
Come per la parabola e per l'ellisse, anche per l'iperbole, mostriamo come sia possibile dedurre le equazioni parametriche che descrivono la curva inviluppo della famiglia di rette. I calcoli sono del tutto analoghi a quelli svolti per l'ellisse e si fondano sulla risoluzione del sistema di equazioni \begin{equation}\cases{F(x,y,t)=0\cr\cr {{\rm d}F\over{\rm d}t}=0\cr}\label{eq:1}\end{equation} già discusso e introdotto nello studio della parabola. Ricordiamo quindi che in tale sistema la prima equazione rappresenta la forma implicita della funzione che descrive la famiglia di curve (nel nostro caso sono, come visto nella precedente sezione, delle rette) e la seconda è invece la derivata di tale funzione eseguita rispetto al solo parametro t.
Figura 3.15. iperbole15.ggb.
Riferendoci alla fig. 3.15 scegliamo sia quindi \(AB=a\), \(E(-c,0)\) e dove, come evidenziato nella costruzione, \(c>a\). Scelto come parametro l'angolo \(\gamma=\angle BAG\) le coordinate di \(G\) sono \(G(a \cos\gamma, a\sin\gamma)\) e conseguentemente il coefficiente angolare della retta \(EG\) è ancora \begin{equation}m_{EG}={y_G-y_E\over x_G-x_E}={a\sin\gamma\over a\cos\gamma+c}.\end{equation} Ne segue l'equazione della famiglia di rette tangenti \begin{equation}y-y_G=-{1\over m_{EG}}(x-x_G)\quad\Rightarrow\quad y-a\sin\gamma=-{a\cos\gamma+c\over a\sin\gamma}(x-a\cos\gamma)\end{equation} che scriviamo in forma implicita definendo nel contempo la funzione \begin{equation}F(x,y,\gamma)=a y\sin\gamma +a(x-c)\cos\gamma+cx-a^2=0.\label{eq:4}\end{equation} La derivata prima di tale funzione eseguita rispetto a \(\gamma\) ha la forma \begin{equation}{{\rm d}F\over{\rm d}\gamma}=ay\cos\gamma-a(x-c)\sin\gamma\end{equation} cosicché, il sistema \eqref{eq:1} risulta \begin{equation}\cases{a y\sin\gamma +a(x-c)\cos\gamma+cx-a^2=0\cr ay\cos\gamma-a(x-c)\sin\gamma=0.\cr}\end{equation} Esplicitata dalla seconda l'incognita y\begin{equation}y={(x-c)\sin\gamma\over \cos\gamma}\end{equation} e sostituita nella prima \begin{equation}{a(x-c)\sin^2\gamma\over\cos\gamma}+ax\cos\gamma-ac\cos\gamma+cx-a^2=0,\end{equation} moltiplichiamo entrambi i membri per \(\cos\gamma\) \begin{equation}ax\sin^2\gamma-ac\sin^2\gamma+ax\cos^2\gamma-ac\cos^2\gamma+cx\cos\gamma-a^2\cos\gamma=0,\end{equation} applichiamo l'identità goniometrica fondamentale \begin{equation}ax(\sin^2\gamma+\cos^2\gamma)-ac(\sin^2\gamma+\cos^2\gamma)+cx\cos\gamma=a^2\cos\gamma,\end{equation} e raccogliamo a fattore i termini comuni \begin{equation}x(a+c\cos\gamma)=a(c+a\cos\gamma).\end{equation} Diviso per \(a+c\cos\gamma\not=0\), otteniamo infine la soluzione \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{x={a(c+a\cos\gamma)\over a+c\cos\gamma}\qquad y={(a^2-c^2)\sin\gamma\over a+c\cos\gamma}}\label{eq:12}\end{equation} che possiamo interpretare come la rappresentazione parametrica dell'inviluppo.
Nella figura 3.16 che segue, tutti gli elementi, sia quelli costruttivi quali a e c, sia il parametro \(\gamma\) sono associati a degli slider in modo da poter visualizzare il comportamento della famiglia \eqref{eq:4} e della curva inviluppo \eqref{eq:12} (introdotta dalla barra d'inserimento tramite il comando Curva[]).
Figura 3.16. iperbole16.ggb.
Approfondimento. Equazione canonica
Intendiamo in questa sezione dedurre dalle equazioni \eqref{eq:12} l'equazione canonica dell'iperbole. Dalla prima ricaviamo quindi il rapporto \begin{equation}{x\over a}={c+a\cos\gamma\over a+c\cos\gamma}\label{eq:13}\end{equation} ed eseguiamo il quadrato della seconda \begin{equation}y^2={(a^2-c^2)^2\sin^2\gamma\over (a+c\cos\gamma)^2}.\label{eq:14}\end{equation} Quadrando ora pure la \eqref{eq:13} \begin{equation}{x^2\over a^2}={(c+a\cos\gamma)^2\over (a+c\cos\gamma)^2}\end{equation} e divisi entrambi i membri della \eqref{eq:14} per \(a^2-c^2\) \begin{equation}{y^2\over a^2-c^2}={(a^2-c^2)\sin^2\gamma\over (a+c\cos\gamma)^2}\end{equation} non ci resta che sommare membro a membro queste due ultime relazioni \begin{equation}{x^2\over a^2}+{y^2\over a^2-c^2}={c^2+2ac\cos\gamma+a^2\cos^2\gamma+a^2\sin^2\gamma-c^2\sin^2\gamma\over (a+c\cos\gamma)^2}\end{equation} ossia \begin{equation}{x^2\over a^2}+{y^2\over a^2-c^2}={c^2(1-\sin^2\gamma)+2ac\cos\gamma+a^2(\cos^2\gamma+\sin^2\gamma)\over (a+c\cos\gamma)^2}.\end{equation} L'identità fondamentale della goniometria permette ora di semplificare la precedente in \begin{equation}{x^2\over a^2}+{y^2\over a^2-c^2}={c^2\cos^2\gamma+2ac\cos\gamma+a^2\over (a+c\cos\gamma)^2}\end{equation} e, notato come il numeratore del secondo membro sia lo sviluppo del denominatore, otteniamo in conclusione \begin{equation}{x^2\over a^2}+{y^2\over a^2-c^2}=1\end{equation} e dato che \(c>a\), anche \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{{x^2\over a^2}-{y^2\over c^2-a^2}=1,}\end{equation} che è l'equazione aspettata di una iperbole con asse focale coincidente con l'asse delle ascisse e semiassi \(a\) e \(b=\sqrt{c^2-a^2}\).