Parabola: costruzione n. 4
Diversamente dalle precedenti costruzioni dove si determinava geometricamente un punto appartenente ad una parabola, in questa costruzione giungeremo alla parabola attraverso la rappresentazione grafica dell'insieme (più correttamente, di un sottoinsieme) delle sue rette tangenti. Intediamo cioè individuare la parabola come inviluppo delle sue rette tangenti.
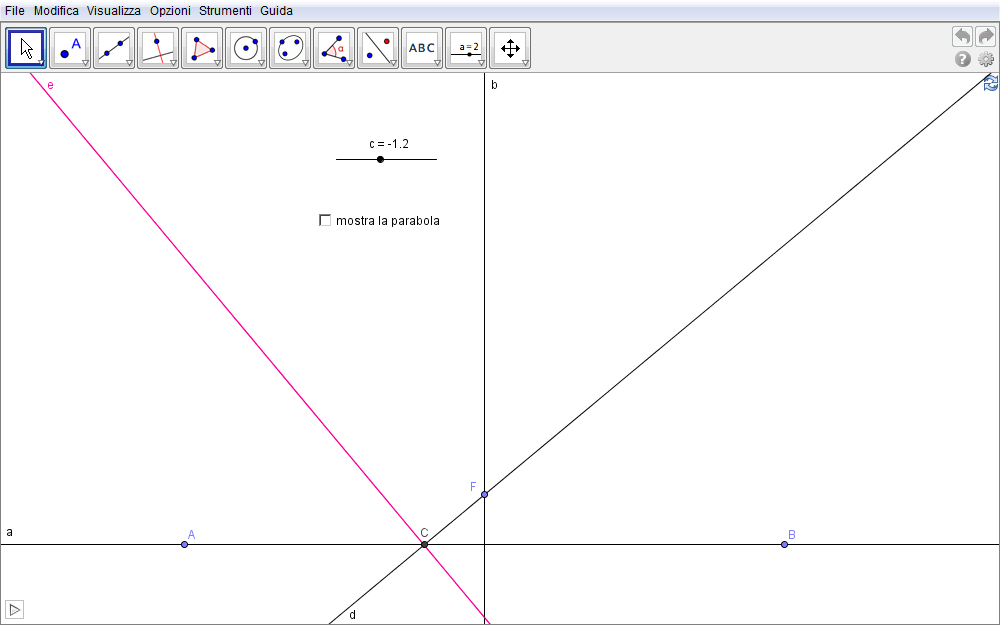
- Tracciata una retta orizzontale a che, per semplicità facciamo coincidere con l'asse x del sistema cartesiano associato alla vista grafica (Visualizza/Assi) (fig. 1.7),
- sia F (il fuoco) un punto qualsiasi non appartenente ad a (per simmetria appartenente all'asse y) e
- sia b la retta per esso perpendicolare ad a, cioè l'asse y. Tale retta rappresenterà pure l'asse della parabola.
- Inserito uno slider c
 numerico variabile tra gli estremi -10, +10 con incremento di 0.1,
numerico variabile tra gli estremi -10, +10 con incremento di 0.1,
- immettiamo tramite la barra di inserimento algebrico il punto C=(c,0).
- Costruita la retta d passante per F e C,
- sia e la retta perpendicolare a d e passante per H . È questa retta che risulta tangente alla parabola in un suo punto.
- Difatti, attivata la traccia di d (clic destro, Traccia attiva) e
- avviata l'animazione dello slider,
al variare di C su a, la famiglia di rette e fa emergere il profilo di una parabola che si identifica come l'inviluppo dell'insieme di rette. Selezionare la casella di controllo mostra la parabola per evidenziare il luogo ottenuto. Per inviluppo intendiamo quindi
una curva che sia tangente in qualche punto ad ogni membro di una data famiglia di curve.
Figura 1.7. parabola07.ggb.
La determinazione del punto di tangenza appartenente alla parabola si può ottenere con la costruzione geometrica descritta di seguito.
- Tracciata la retta h parallela ad a avente distanza da quest'ultima pari alla distanza di F da a (h rappresenta la direttrice della parabola, fig. 1.8), sia
- G il suo punto di intersezione con la retta d. Questo permette di riconoscere (con il teorema di Talete) la congruenza dei due segmenti CF e CG e quindi la retta tangente e è l'asse di FG.
- Se ora si conduce la perpendicolare a h per G,
- questa incontra la retta e nel punto P appartenente alla parabola.
Figura 1.8. parabola08.ggb.
Attivare l'animazione per visualizzare la traccia dei punti P. Difatti i due triangoli rettangoli CGP e CFP sono congruenti per cui PF = PG e quindi P dista egualmente da F e dalla retta h (si veda la definizione di parabola). Va notato come quest'ultima costruzione sia riconducibile sostanzialmente alla prima costruzione di questa serie nella quale il punto qui indicato con G era invece là il punto variabile.
Espressione analitica della famiglia di rette e della parabola inviluppo
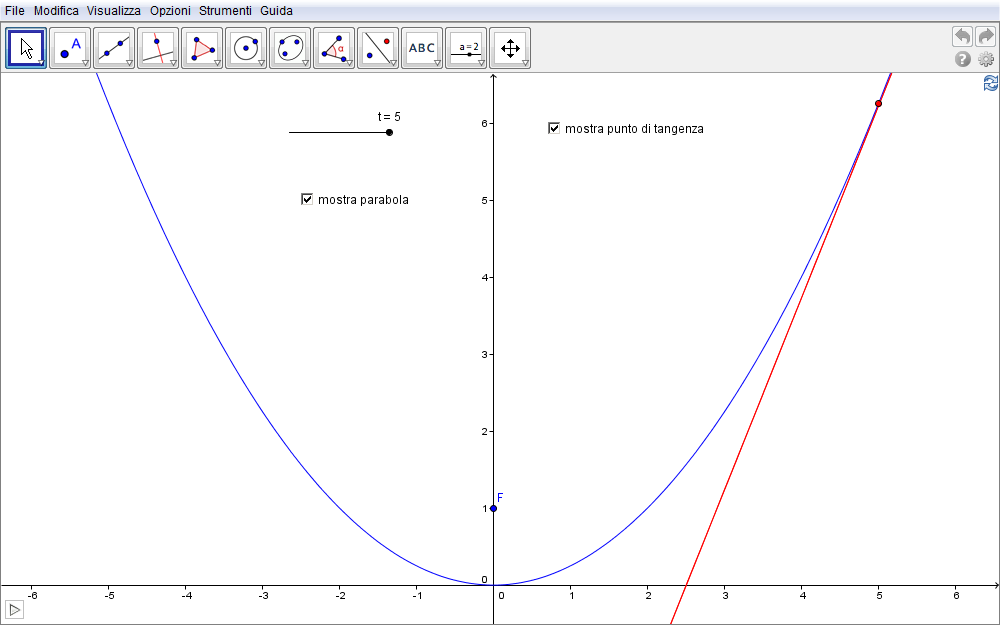
Sulla base delle costruzioni geometriche precedenti intendiamo ora dedurre le espressioni analitiche sia della famiglia di rette tangenti alla parabola sia della parabola stessa. Introdotto pertanto un sistema cartesiano con origine nel punto D della figura precedente, siano \(F(0,f)\) le coordinate del fuoco mentre l'ascissa del punto P sia rappresentata dal parametro \(x_P=t\). Per determinare l'ordinata di tale punto va innanzitutto ottenuta l'equazione della retta CP, perpendicolare alla retta FG e asse del segmento FG. Poiché il punto G appartenente alla retta direttrice di equazione \(y=-f\) ha, per costruzione, le coordinate \(G(t,-f)\), il punto medio C di FG è individuato dalla coppia \(C({t\kern1pt/2},0)\). Il coefficiente angolare di CF risulta pertanto \begin{equation}m_{CF}={y_F-y_C\over x_F-x_C}={f-0\over 0-(t\kern1pt/ 2)}=-{2f\over t}\end{equation} e l'equazione della retta CP è invece \begin{equation}CP:y-y_C=-{1\over m_{CF}}(x-x_C)\quad\Rightarrow\quad y-0=\biggl({t\over 2f}\biggr)\biggl(x-{t\over 2}\biggr)\end{equation} da cui \begin{equation}CP: y=\biggl(\!{t\over 2f}\biggr)x-{t^2\over 4f}.\label{eq:tre}\end{equation} Quest'ultima equazione rappresenta quindi la famiglia di rette cercata in funzione del parametro \(t\). L'equazione della parabola inviluppo ne discende immediatamente non appena determiniamo l'ordinata corrispondente all'ascissa \(x_P=t\) e ciò si ottiene eliminando \(t\) nella precedente equazione \eqref{eq:tre} \begin{equation}y=\biggl(\!{x\over 2f}\!\biggr)x-{x^2\over 4f}\quad\Rightarrow\quad y=\biggl(\!{1\over 2f}\!\biggr)x^2-{x^2\over 4f}=\biggl(\!{1\over 4f}\!\biggr)x^2.\end{equation} L'equazione cercata è quindi \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{y=\biggl(\!{1\over 4f}\!\biggr)x^2.}\label{eq:5}\end{equation} Possiamo ora riprodurre la precedente costruzione geometrica sfruttando le conoscenze analitiche appena dedotte e quindi disporre di una conferma visiva della correttezza di quanto fatto. Nella figura 1.9 abbiamo pertanto introdotto uno slider per rappresentare i valori del parametro t e quindi, fissato \(f=1\), immettiamo nella barra di inserimento di GeoGebra le equazioni \eqref{eq:tre} e \eqref{eq:5}, rispettivamente per la famiglia di rette e per la parabola. Infine immettiamo il punto di tangenza \(P(t,(1/4) t^2)\) e avviamo l'animazione.
Figura 1.9. parabola09.ggb.
Approfondimento. Ricerca dell'inviluppo
Nella sezione precedente siamo stati in grado di giungere all'equazione della curva inviluppo in quanto ci era nota l'ascissa del punto di tangenza tra l'inviluppo e la famiglia di tangenti. Non è questo comunque il caso generale per cui il punto di tangenza non si conosce a priori. Cerchiamo quindi un metodo che prescinda da questo dato. A tale scopo riprendiamo l'equazione \eqref{eq:tre} e, trasportata la y a secondo membro, definiamo la funzione \begin{equation}F(x,y,t)=\biggl(\!{t\over 2f}\biggr) x-y-{t^2\over 4f}.\label{eq:sei}\end{equation} Evidentemente se si pone \(F(x,y,t)=0\) questa equazione esprime, al variare di t, la famiglia di rette tangenti già discussa.
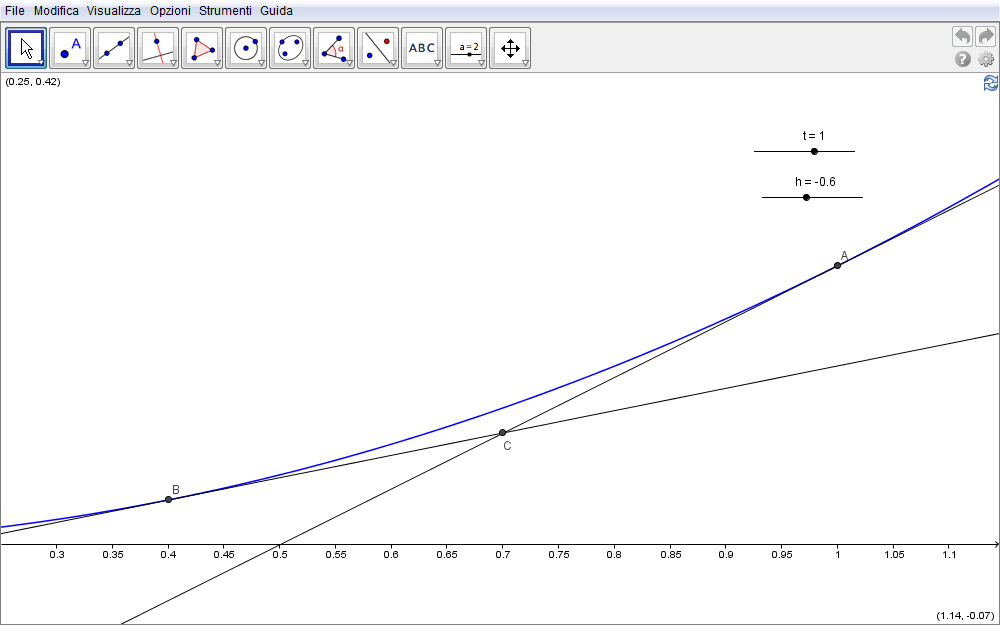
Consideriamo ora due rette qualsiasi di questa famiglia, la prima corrispondente al parametro t, la seconda al parametro t + h e chiamiamo h incremento della variabile t. Nella figura 1.10 seguente, dove appare in colore pure la parabola inviluppo (con \(f=1\)) i valori t e h sono associati a due slider.
Figura 1.10. parabola10.ggb.
Entrambe le rette sono tangenti alla curva inviluppo: la prima retta tocca la parabola nel punto A mentre la seconda nel punto B. Queste due rette si intersecano nel punto C che, da come appare nella figura 1.10, non appartiene all'inviluppo. Se però riduciamo il valore di h facendolo tendere allo zero (e nel contempo aumentando lo zoom in GeoGebra) possiamo intuire come questo punto debba, al limite \(h\to 0\), appartenere alla curva inviluppo. Vediamo di confermare o meno queste osservazioni determinando innanzitutto le coordinate di C e quindi studiando il loro comportamento per \(h\to 0\). Dobbiamo pertanto risolvere il sistema \begin{equation}\cases{F(x,y,t)=0\cr F(x,y,t+h)=0\cr}\label{eq:7}\end{equation} ed esplicitamente \begin{equation}\cases{\biggl(\!{t\over 2f}\biggr) x-y-{t^2\over 4f}=0\cr\cr \biggl(\!{t+h\over 2f}\biggr) x-y-{(t+h)^2\over 4f}=0.\cr}\label{eq:8}\end{equation} Moltiplicando la prima per \(-1\), sommando membro a membro e risolvendo in \(x\) si ottiene \begin{equation}{h\over 2f}\,x+{t^2\over 4f}-{(t+h)^2\over 4f}\quad\Rightarrow\quad x={2t+h\over 2}.\end{equation} Sostituito questo risultato nella prima delle \eqref{eq:8}, l'ordinata di C risulta \begin{equation}y={t\over 2f}\cdot\biggl({2t+h\over 2}\biggr)-{t^2\over 4f}\quad\Rightarrow\quad y={t^2+th\over 4f}.\end{equation} Se ora facciamo tendere allo zero h, questa coppia di coordinate converge verso i valori \begin{equation}h\to0\qquad x_C={2t+h\over 2}\to {2t\over 2}=t,\qquad y_C={t^2+t h\over 4f}\to {t^2\over 4f}\end{equation} e quindi il punto che in coerenza con la sezione precedente, rinominiamo P, possiede coordinate \begin{equation}x_P=t,\qquad y_P= {t^2\over 4f}.\end{equation} Queste due equazioni costituiscono la rappresentazione parametrica del luogo dei punti P. È comunque immediato ottenere l'equazione implicita della curva eliminando la dipendenza dal parametro t: si ottiene in tal modo la \eqref{eq:5}\begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{y=\biggl(\!{1\over 4f}\!\biggr)x^2},\end{equation} risultato che conferma come P appartenga alla parabola inviluppo.
Approfondimento. Conferma e formalizzazione del metodo
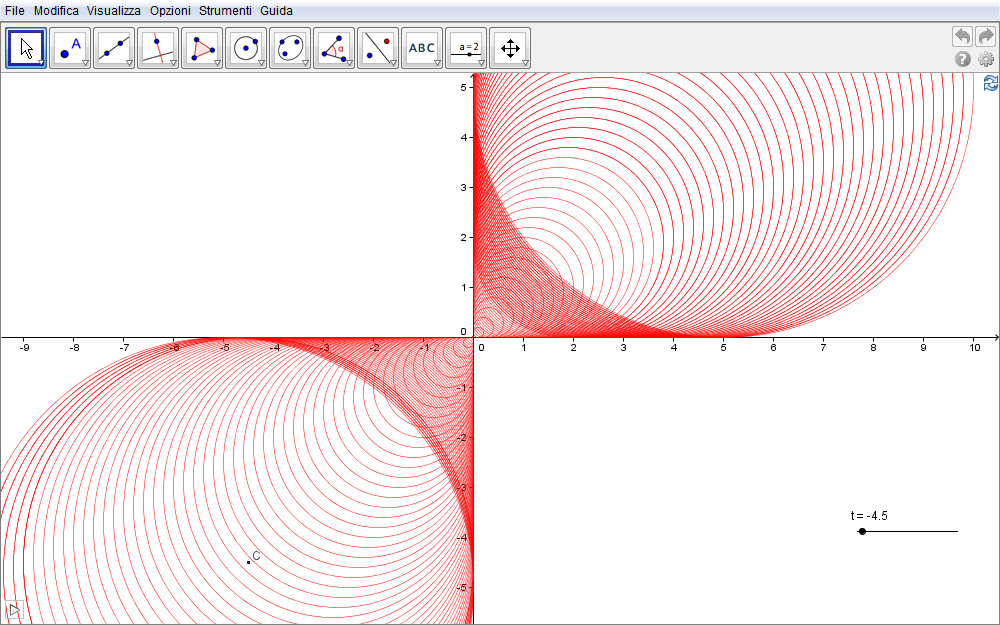
Quale conferma del metodo appena sviluppato intendiamo costruire una famiglia di circonferenze tangenti contemporaneamente agli assi coordinati cosicché il loro inviluppo sia noto a priori essendo costituito dagli stessi assi coordinati (fig. 1.11).
Figura 1.11. parabola11.ggb.
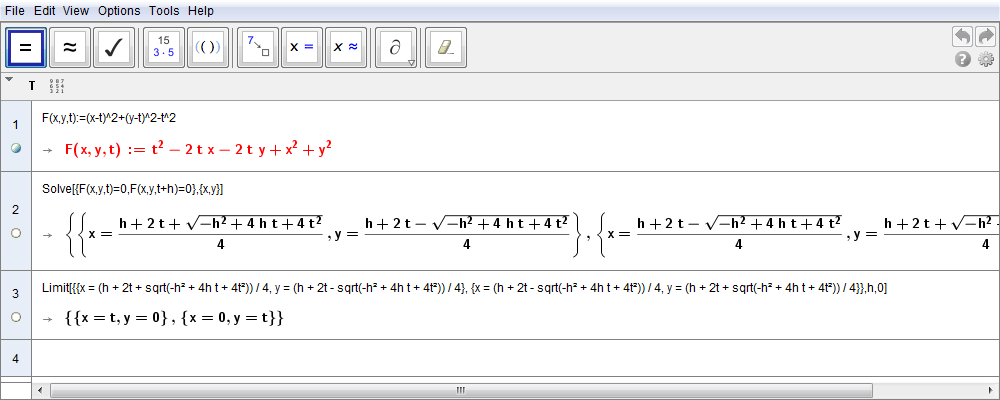
Se imponiamo che il centro C della famiglia abbia coordinate \(C(t,t)\) e quindi appartenga alla bisettrice del I e III quadrante, il raggio di ciascuna circonferenza sarà pari a \(|t|\). L'equazione della famiglia di circonferenze è allora \begin{equation}(x-t)^2+(y-t)^2=t^2,\end{equation} espressione che suggerisce di introdurre la funzione \begin{equation}F(x,y,t)=(x-t)^2+(y-t)^2-t^2.\label{eq:15}\end{equation} Se consideriamo \(h\) come un incremento qualsiasi di t, la corrispondente circonferenza sarà \(F(x,y,t+h)=(x-t-h)^2+(y-t-h)^2-(t+h)^2=0\). Dobbiamo pertando risolvere il sistema \begin{equation}\cases{F(x,y,t)=0\cr F(x,y,t+h)=0\cr}\quad\Rightarrow\quad \cases{(x-t)^2+(y-t)^2-t^2=0\cr (x-t-h)^2+(y-t-h)^2-(t+h)^2=0\cr}\label{eq:16}\end{equation} ma, in questo caso, intendiamo evitare i calcoli, pur concettualmente semplici (è un sistema di II grado), e sfruttiamo invece la vista CAS di GeoGebra. Pertanto introdotta la funzione \eqref{eq:15} e immesso il comando Risolvi[{F(x,y,t)=0,F(x,y,t+h)=0},{x,y}] otteniamo quanto mostrato in fig. 1.12.
Figura 1.12. parabola12.ggb.
Osserviamo come la coppia di soluzioni (simmetriche in quanto tale è il sistema \eqref{eq:16}) non presenta particolari problemi nel calcolo (intuitivo) del limite \(h\to 0\): difatti in questo limite risulta \begin{equation}h\to 0\quad x={1\over 4}\bigl(h+2t+\sqrt{-h^2+4ht+4t^2}\bigr)\to{1\over 4}\bigl(2t+\sqrt{4t^2}\bigr)= t,\qquad y={1\over 4}\bigl(h+2t-\sqrt{-h^2+4ht+4t^2}\bigr)\to{1\over 4}\bigl(2t-\sqrt{4t^2}\bigr)=0,\end{equation} e le soluzioni sono le coppie \begin{equation}\cases{x=t\cr y=0,\cr}\qquad \cases{x=0\cr y=t\cr}\label{eq:18}\end{equation} che, manifestamente, rappresentano gli assi cartesiani. Un'ulteriore e definitiva conferma la si ottiene pure utilizzando la funzione Limite[] di GeoGebra come mostra la fig. 1.12.
A questo punto non ci rimane che formalizzare il metodo finora seguito riportandolo a nozioni tipiche dell'Analisi. Con riferimento al sistema \eqref{eq:7} (o il primo delle \eqref{eq:16}) e notato che \(F(x,y,t)=0\), possiamo riscrivere la seconda equazione del sistema come \begin{equation}\cases{F(x,y,t)=0\cr F(x,y,t+h)-F(x,y,t)=0\cr}\end{equation} ma, supposto \(h\not=0\), pure come \begin{equation}\cases{F(x,y,t)=0\cr \cr {F(x,y,t+h)-F(x,y,t)\over h}=0.\cr}\end{equation} La riscrittura ottenuta per la seconda equazione mette in evidenza come a primo membro si possa riconoscere il rapporto incrementale della funzione \(F(x,y,t)\) eseguito rispetto alla variabile t e corrispondente all'incremento h. Poiché la curva inviluppo si è ottenuta studiando il limite delle soluzioni del sistema per \(h\to 0\), possiamo aggiungere tale informazione scrivendo \begin{equation}\cases{F(x,y,t)=0\cr \cr \lim_{h \to 0}{F(x,y,t+h)-F(x,y,t)\over h}=0.\cr}\end{equation} Nell'ipotesi che il limite suddetto esista e sia finito sappiamo che esso rappresenta la derivata della funzione \(F\) eseguita rispetto alla sola variabile t (mentre x e y vanno considerate come costanti) per cui in definitiva il sistema diviene \begin{equation}\cases{F(x,y,t)=0\cr \cr {{\rm d}F(x,y,t)\over {\rm d}t}=0\cr}\end{equation} o, più correttamente, introdotto il simbolo \(\partial\) di derivata parziale, \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{F(x,y,t)=0\cr \cr {\partial F(x,y,t)\over \partial t}=0.\cr}}\end{equation}
Alla luce di tale importante risultato gli inviluppi studiati in questa pagina discendono a questo punto immediati: per la parabola ripresa la \eqref{eq:sei} ed eseguendone la derivata rispetto a t (le altre variabili, lo ripetiamo, vanno considerate come delle costanti), abbiamo\begin{equation}{\partial F(x,y,t)\over \partial t}={x\over 2f}-0-{2t\over 4f}=0\quad\Rightarrow\quad {x\over 2f}={t\over 2f} \quad\Rightarrow\quad x=t,\end{equation} e quindi il sistema è\begin{equation}\cases{F(x,y,t)=\biggl(\!{t\over 2f}\biggr) x-y-{t^2\over 4f}=0\cr \cr x=t}\quad\Rightarrow\quad \cases{y={t^2\over 4f}\cr\cr x=t\cr}\quad\Rightarrow\quad y=\biggl(\!{1\over 4f}\!\biggr)x^2.\end{equation} Nel caso della famiglia \eqref{eq:15}, la derivata rispetto a t è \begin{equation}{\partial F(x,y,t)\over \partial t}=-2(x-t)-2(y-t)-2t=0\quad\Rightarrow\quad x+y-t=0\end{equation} e il sistema \begin{equation}\cases{(x-t)^2+(y-t)^2-t^2=0\cr x+y-t=0\cr}\end{equation} si risolve facilmente \begin{equation}y-t=-x\quad\Rightarrow\quad (x-t)^2+(-x)^2-t^2=0\quad\Rightarrow\quad 2x^2-2xt=0\quad\Rightarrow\quad x=0,\quad x=t\end{equation}confermando le soluzioni \eqref{eq:18} già ottenute per altra via.