Iperbole: costruzione n. 3
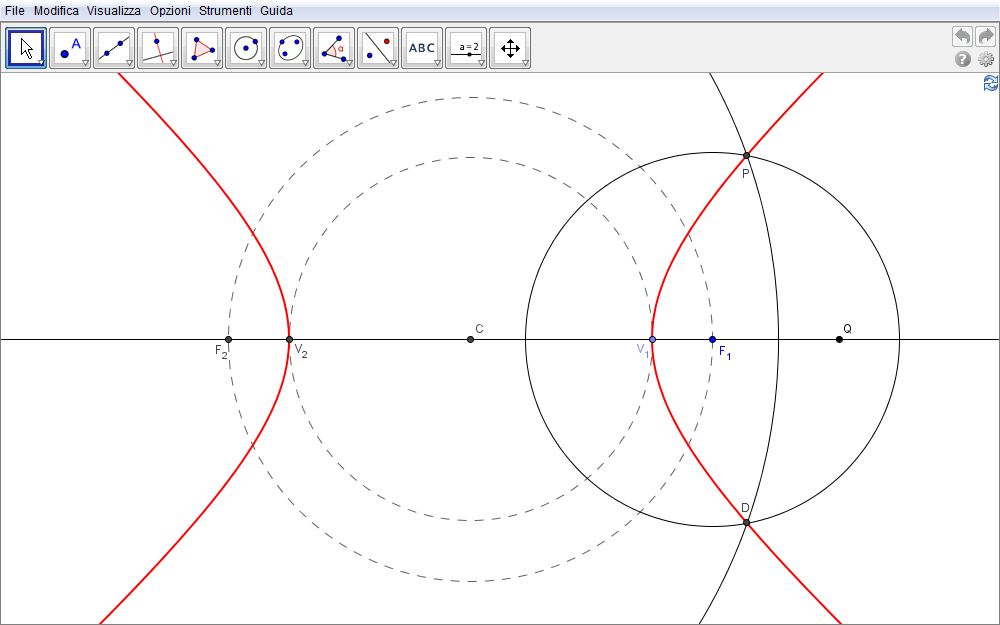
- Il primo passo della costruzione consiste nel tracciare una retta e quindi,
- considerato un suo punto C (fig. 3.5),
- costruire la circonferenza di centro C avente un dato raggio.
- Questa incontra la retta in due punti, \(F_1\) e \(F_2\) che saranno i fuochi dell'iperbole.
- Con lo stesso centro C si tracci una seconda circonferenza di raggio inferiore alla precedente e siano \(V_1\) e \(V_2\) le sue intersezioni con la retta originaria.
- Sia Q un punto qualsiasi non appartenente al segmento \(F_1F_2\).
- Si tracci ora la circonferenza di centro \(F_2\) e raggio pari alla
lunghezza di \(V_2Q\)
 .
.
- Allo stesso modo si tracci la circonferenza di centro \(F_1\) e raggio \(V_1Q\).
Evidentemente i punti di intersezione P e D di queste ultime due circonferenze distano da \(F_1\) una distanza pari a \(V_1Q\) e da \(F_2\) la lunghezza di \(V_2Q\) cosicché la loro differenza (in valore assoluto) risulta \begin{equation}\bigl|PF_1-PF_2\bigr|=\bigl|V_1Q-V_2Q\bigr|=V_1V_2\label{eq:1}\end{equation} e tale lunghezza rimane costante al variare di Q. I punti P appartengono quindi ad una iperbole in quanto la differenza delle loro distanze da due punti dati è una costante. Al variare del punto Q (lo si trascini nella fig. 3.5) si ottiene il luogo dei punti P cioè l'iperbole cercata.
Figura 3.5. iperbole05.ggb.
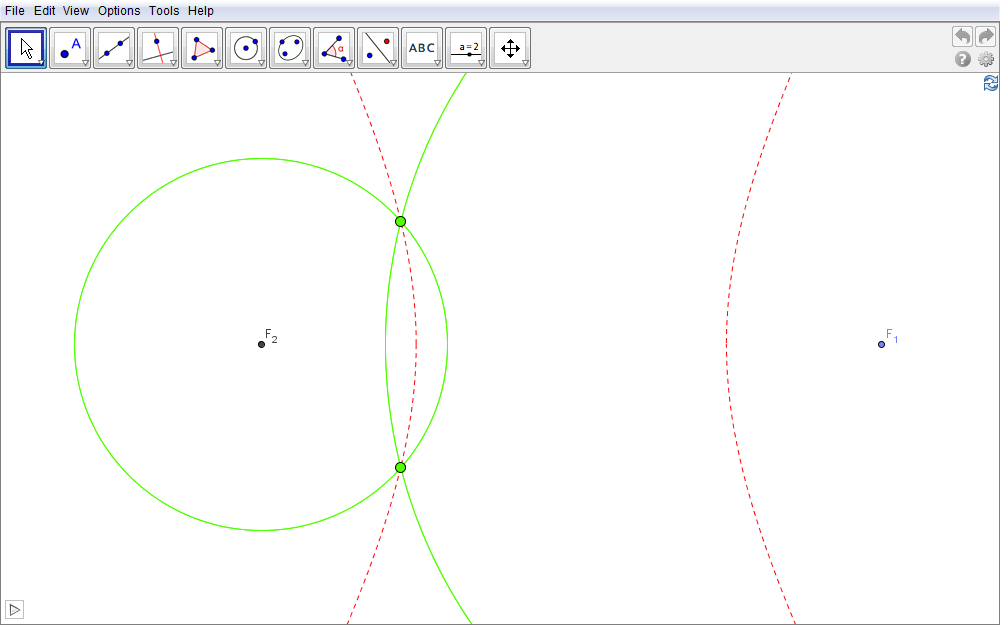
Questa costruzione suggerisce come si possa interpretare l'iperbole anche come il luogo dei punti di intersezione di due famiglie di circonferenze ciascuno con un proprio centro fisso (i fuochi) e tali da avere pari ad una costante la differenza dei rispettivi raggi. Per questo motivo, nell'ambito della fisica ondulatoria, sono delle iperboli le linee di interferenza costruttiva e/o distruttiva di onde emesse da due sorgenti coerenti e con differenza di fase costante nel tempo (avviare l'animazione nella successiva figura 3.6). A tal proposito si veda la sezione finale in questa pagina.
Figura 3.6. iperbole06.ggb.
Deduzione analitica
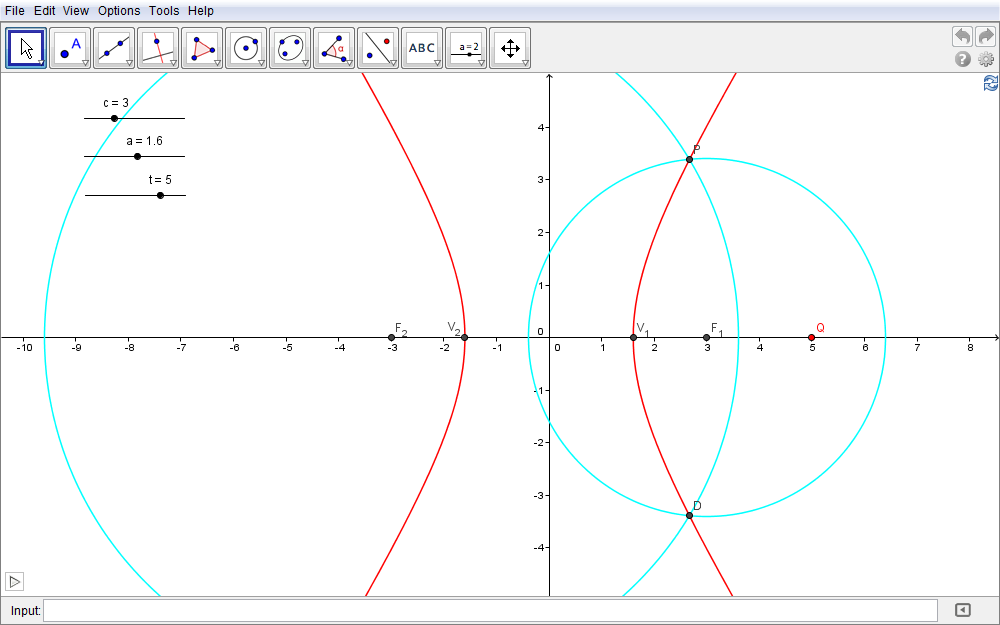
La precedente costruzione riproduce, ancora una volta, quella già proposta per l'ellisse. In quel caso il punto \(Q\) variava entro il segmento \(F_1F_2\) con i vertici \(V_1\) e \(V_2\) esterni a tale segmento. Qui invece è il segmento \(F_1F_2\) che contiene \(V_1V_2\) e \(Q\) non appartiene al segmento \(F_1F_2\). Sfruttando in questa sezione le capacità algebriche di GeoGebra, visualizziamo innanzitutto il sistema cartesiano canonico associato alla costruzione (fig. 3.7) e quindi definiamo lo slider c, variabile tra 0 e 10, e che rappresenterà l'ascissa dei fuochi \(F_1(c,0)\) e di \(F_2(-c,0)\). In corrispondenza lo slider a, variabile tra 0 e c, definirà invece i vertici \(V_1(a,0)\), \(V_2(-a,0)\) (quindi \(V_1V_2=2a\)). Infine associamo allo slider t l'ascissa del punto \(Q\) ossia \(Q(t,0)\) variabile (teoricamente) nell'insieme \(\{t\,\bigl|\bigr.\,t\leq -c \vee t\geq c\}\). Tutti questi punti sono inseriti in GeoGebra tramite la barra di inserimento (fig. 3.7).
Figura 3.7. iperbole07.ggb.
L'equazione della circonferenza di centro \(F_1\) e raggio \(V_1Q=a-t\) è allora \begin{equation}d:(x-c)^2+y^2=(t-a)^2\label{eq:2}\end{equation} mentre quella di centro \(F_2\) e raggio \(V_2Q=t-(-a)=t+a\) risulta \begin{equation}e:(x+c)^2+y^2=(t+a)^2.\label{eq:3}\end{equation} Per determinare i loro punti di intersezione, P e D, dobbiamo evidentemente risolvere il sistema di II grado \begin{equation}\cases{(x-c)^2+y^2=(t-a)^2\cr (x+c)^2+y^2=(t+a)^2\cr}\quad\Rightarrow\quad \cases{x^2+c^2-2cx+y^2=a^2+t^2-2at\cr x^2+c^2+2cx+y^2=a^2+t^2+2at.\cr}\end{equation} Moltiplicando per \(-1\) la prima e sommando in colonna, si ha facilmente \begin{equation}4xc=4at\quad\Rightarrow\quad x={at\over c}.\label{eq:4}\end{equation} Introdotto quest'ultimo risultato nella prima equazione \begin{equation}{a^2t^2\over c^2}+c^2-2c\cdot {at\over c}+y^2=a^2+t^2-2at\quad\Rightarrow\quad {a^2t^2\over c^2}+c^2-2at+y^2=a^2+t^2-2at\end{equation} si giunge dopo qualche calcolo all'equazione \begin{equation}y^2={(c^2-a^2)(t^2-c^2)\over c^2}\label{eq:6}\end{equation} che, date le limitazioni poste \(c\geq a\) e \(t\not\in\,]-c,c\,[\), fornisce le due soluzioni \begin{equation}y=\pm{\sqrt{(c^2-a^2)(t^2-c^2)}\over c}.\end{equation} I punti P e D (fig. 3.7) hanno quindi coordinate \begin{equation}P\biggl({at\over c},{\sqrt{(c^2-a^2)(t^2-c^2)}\over c}\biggr),\qquad D\biggl({at\over c},-{\sqrt{(c^2-a^2)(t^2-c^2)}\over c}\biggr).\end{equation}
Immesse queste espressioni in GeoGebra, deduciamo l'equazione dell'iperbole nella sua forma implicita che è pure quella canonica. A tale scopo riprendiamo i risultati \eqref{eq:4} e \eqref{eq:6} \begin{equation}\cases{x={at\over c}\cr \cr y^2={(c^2-a^2)(t^2-c^2)\over c^2}.\cr}\end{equation} Tale coppia di equazioni esprime l'ascissa e il quadrato dell'ordinata dei punti dell'iperbole in termini del parametro \(t\). Siamo quindi di fronte ad una rappresentazione parametrica di tale curva e pertanto per giungere alla forma implicita dobbiamo eliminare la dipendenza da \(t\). Dalla prima equazione segue quindi \(t=(cx)\,/a\) cosicché la seconda diviene \begin{equation}y^2={(c^2-a^2)(c^2x^2/a^2-c^2)\over c^2}\end{equation} che si semplifica in \begin{equation}y^2=(c^2-a^2)\biggl({x^2\over a^2}-1\biggr).\end{equation} Se dividiamo per \(c^2-a^2\) e ridisponiamo i termini, otteniamo infine \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{{x^2\over a^2}-{y^2\over c^2-a^2}=1.\label{eq:13}}\end{equation} È questa l'equazione del luogo da immettere in GeoGebra per verificare, avviata l'animazione in fig. 3.7, l'appartenenza dei punti P e D all'iperbole. Infine se poniamo \begin{equation}b^2=c^2-a^2\label{eq:14}\end{equation} l'equazione precedente assume la nota forma canonica.
Interferenza
Sulla base delle precedenti deduzioni, prima geometrica e poi analitica, vogliamo mostrare qui come le linee di interferenza costruttiva (o, volendo, di interferenza distruttiva) di due sorgenti di onde armoniche che oscillano in fase siano delle iperboli con i fuochi coincidenti con le sorgenti stesse.
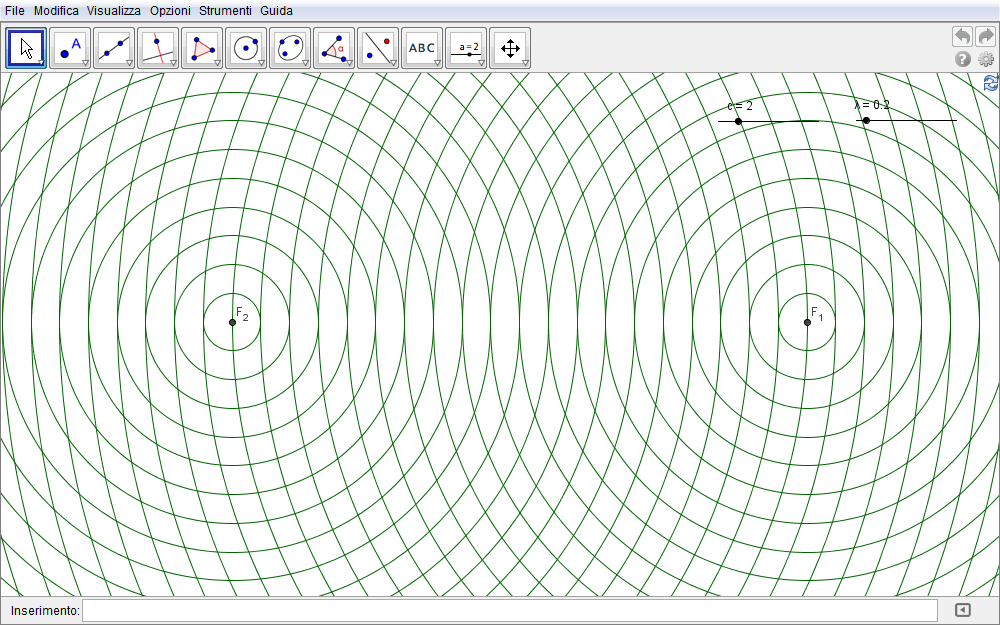
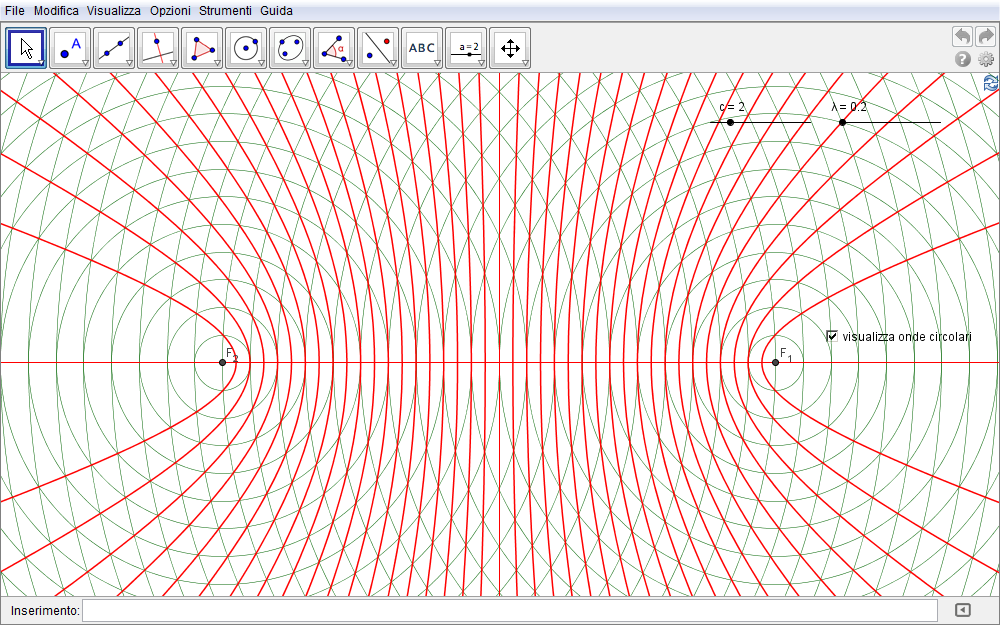
Disponiamo pertanto queste due sorgenti sull'asse x di un sistema cartesiano in punti simmetrici rispetto all'origine: le loro coordinate saranno quindi \(F_1(c,0)\) e \(F_2(-c,0)\) e, come nella precedente sezione, tale parametro lo associamo ad uno slider così da poterlo variare, all'occorrenza, liberamente. Definiamo un secondo slider \(\lambda\) rappresentativo della lunghezza d'onda emessa da ciascuna sorgente e rappresentiamo i fronti d'onda emessi in un certo intervallo di tempo con una famiglia discreta di circonferenze centrata su ciascuna sorgente (fig. 3.8): in GeoGebra questa famiglia è immessa come Successione[(x - c)^2 + y^2 = (i λ)^2, i, 1, 30] e analogamente per l'altra sorgente. Supponiamo che queste circonferenze (o fronti d'onda) rappresentino, in un dato istante, i massimi della perturbazione per cui nel seguito individueremo, come detto, i punti di interferenza costruttiva.
Figura 3.8. iperbole08.ggb.
In analogia alle equazioni \eqref{eq:2} e \eqref{eq:3}, le equazioni dei due insiemi di fronti d'onda sono \begin{equation}\cases{(x-c)^2+y^2=(n_1\lambda)^2\cr (x+c)^2+y^2=(n_2\lambda)^2,\cr}\end{equation} essendo \begin{equation}r_1=n_1 \lambda,\qquad r_2=n_2\lambda,\qquad n_1,\ n_2\in \{0,1,2,\dots\}\end{equation} i raggi di ciascun fronte evidentemente multipli interi della lunghezza d'onda. I punti di intersezione tra questi fronti d'onda saranno quindi pure i punti di interferenza costruttiva in quanto le due pertubazioni assumono ivi il loro massimo. La condizione che individua l'iperbole è in base alla \eqref{eq:1}, la costanza della differenza dei due raggi cioè delle distanze dei fronti d'onda dalle sorgenti. Sappiamo che tale costante è pari alla distanza \(V_1V_2=2a\) tra i vertici per cui, formalmente, \begin{equation}2a=\bigl|r_2-r_1\bigr|=\bigl|n_2\lambda-n_1\lambda\bigr|=\lambda\bigl|n_2-n_1\bigr|\end{equation} da cui \begin{equation}a={\lambda\over 2}\bigl|n_2-n_1\bigr|.\end{equation} Determinato \(a\), diviene possibile scrivere l'equazione canonica delle iperboli in quanto \(c\) è pure noto e \(b^2\) è definito dalla \eqref{eq:14}. Pertanto \begin{equation}b^2=c^2-a^2= c^2-\biggl({\lambda\over 2}\bigl|n_2-n_1\bigr|\biggr)^{\kern-2pt 2}=c^2-{\lambda^2\over 4}(n_2-n_1)^2\end{equation} e l'equazione canonica delle iperboli risulta \begin{equation}{x^2\over \bigl[{\lambda^2\over 4}(n_2-n_1)^2\bigr]}-{y^2\over \bigl[c^2-{\lambda^2\over 4}(n_2-n_1)^2\bigr]}=1.\end{equation} Se introduciamo il numero intero \(n\) pari alla differenza \begin{equation}n=n_2-n_1\end{equation} \begin{equation}{x^2\over \bigl({\lambda^2\over 4}n^2\bigr)}-{y^2\over \bigl(c^2-{\lambda^2\over 4}n^2\bigr)}=1\label{eq:22}\end{equation} appare con maggior evidenza come ciascuna iperbole caratterizzante i punti di interferenza costruttiva dipenda dall'intero \(n\) e quindi appartenga ad una famiglia discreta di iperboli. Posta la condizione \begin{equation}c^2-{\lambda^2\over 4}n^2\geq 0\end{equation} che assicura che l'equazione \eqref{eq:22} sia effettivamente un'iperbole (viceversa si ottengono delle ellissi), \begin{equation}n\leq {2c\over \lambda},\end{equation} possiamo utilizzare direttamente l'equazione \eqref{eq:22} o in alternativa, il comando di GeoGebra, iperbole[fuoco1,fuoco2,semiasseFocale] per visualizzare, al variare di \(n\), una successione di iperboli di interferenza costruttiva (in particolare, variare nella fig. 3.9 il parametro \(\lambda\)).
Figura 3.9. iperbole09.ggb.