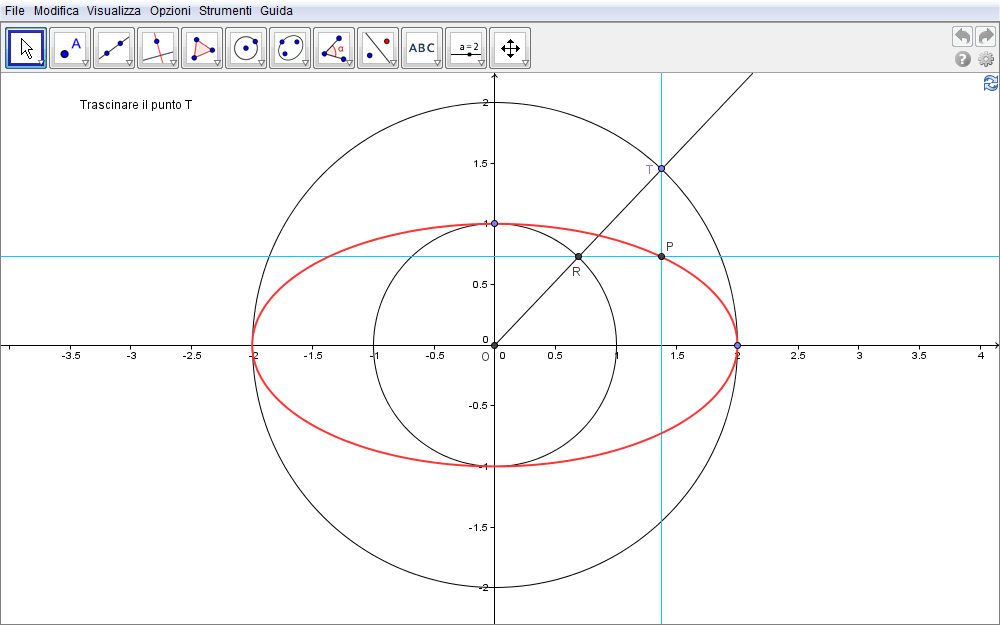
Ellisse: costruzione n. 3
- Tracciati due assi perpendicolari che si intersecano nel punto O (fig. 2.8),
- si aggiungono due circonferenze aventi centro in O e di raggio diverso. Come vedremo, a ciascun raggio sarà associata la lunghezza di un semiasse dell'ellisse.
- Successivamente si traccia una semiretta qualsiasi OT per il loro centro comune,
- semiretta che interseca la circonferenza di raggio maggiore appunto in T e quella di raggio minore in R.
- Tracciata una retta per R parallela alla retta orizzontale,
- si costruisca la retta per T perpendicolare ad essa.
- Sia P il loro punto di intersezione.
Il luogo di questi punti è l'ellisse di semiassi pari ai raggi delle due circonferenze.
Figura 2.8. ellisse08.ggb.
Dimostrazione
In riferimento alla figura seguente la dimostrazione dell'appartenenza di P ad un'ellisse si ottiene facilmente se, introdotta la figura in un sistema cartesiano di origine O e con assi coincidenti con le due rette perpendicolari definite inizialmente, consideriamo la similitudine dei triangoli OHR e OKT.
Figura 2.9. ellisse09.ggb.
Discende che \begin{equation}{OH\over OK}={OR\over OT}\quad\Rightarrow\quad OH={OR\cdot OK\over OT}.\end{equation} Poiché OH rappresenta l'ascissa del punto \(R\) e \(OR=b\) e \(OT=a\) sono i raggi delle due circonferenze, possiamo scrivere che \begin{equation}x_R={b\cdot OK\over a}.\end{equation} Inoltre R appartiene alla circonferenza di raggio b per cui le sue coordinate soddisfano all'equazione \begin{equation}x_R^2+y_R^2=b^2\end{equation} e quindi introdotto il risultato precedente si ha \begin{equation}\biggl({b\cdot OK\over a}\biggr)^{\kern-2pt 2}+y_R^2=b^2\quad\Rightarrow\quad{b^2\cdot OK^2\over a^2}+y_R^2=b^2.\end{equation} Tenuto conto che \(OK=x_T\) la precedente diviene \begin{equation}{b^2 x_T^2\over a^2}+y_R^2=b^2\end{equation} dalla quale, dividendo entrambi i membri per \(b^2\) si ottiene \begin{equation}{x_T^2\over a^2}+{y_R^2\over b^2}=1.\end{equation} Per quanto detto, posto \(x_P=x=x_T\) e \(y_P=y=y_R\) si giunge infine all'equazione rappresentativa del luogo dei punti P \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{{x^2\over a^2}+{y^2\over b^2}=1}\label{eq:7}\end{equation} che rappresenta l'equazione canonica dell'ellisse riportata, di norma, nei testi.
Rappresentazione parametrica dell'ellisse
Riprendiamo la figura precedente evidenziando nella successiva l'angolo \(\alpha=\angle KOT=\angle HOR\) comune ai triangoli \(KOT\) e \(HOR\).
Figura 2.10. ellisse10.ggb.
Intendiamo esprimere le coordinate di P in termini dell'angolo \(\alpha\). Ricordato che \(OT=a\) e \(OR=b\) sono le ipotenuse dei triangoli rettangoli \(KOT\) e \(HOR\), discende \begin{equation}OK=OT\cos\alpha=a\cos\alpha,\quad HR=OR\sin\alpha=b\sin\alpha.\end{equation} Le coordinate di P sono quindi \begin{equation}x_P=OK=a\cos\alpha,\quad y_P=KP=HR=b\sin\alpha.\end{equation} Il sistema di equazioni \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x=a\cos\alpha\cr y=b\sin\alpha\cr}}\label{eq:10}\end{equation} si può intepretare come la rappresentazione parametrica dell'ellisse in quanto fornisce, al variare del parametro \(\alpha\), le coordinate di un suo punto. Da questa rappresentazione deriva facilmente la rappresentazione implicita data dall'equazione \eqref{eq:7} della sezione precedente. Difatti dividendo rispettivamente per \(a\) e \(b\) le \eqref{eq:10} \begin{equation}{x\over a}=\cos\alpha,\quad {y\over b}=\sin\alpha,\end{equation} l'identità goniometrica fondamentale assicura che \begin{equation}\cos^2\alpha+\sin^2\alpha=1\quad\Rightarrow\quad \biggl({x\over a}\biggr)^{\kern-2pt 2}+\biggl({y\over b}\biggr)^{\kern-2pt 2}=1\quad\Rightarrow\quad {x^2\over a^2}+{y^2\over b^2}=1.\end{equation}