Esperienze di Fisica
Interferenza di due sorgenti coerenti ed intensità
In questa pagina deduciamo inizialmente l'equazione che descrive la propagazione di un'onda sferica e quindi, su tale base, affrontiamo il calcolo matematico della distribuzione spaziale dell'intensità dovuta all'interferenza di due
sorgenti armoniche sferiche. Si discutono successivamente le conseguenze fisiche di tale distribuzione trattando in particolare lo studio dell'interferenza in punti molto distanti dalle sorgenti e, infine, nell'ipotesi di onde piane.
Si presentano quindi le caratteristiche di due simulazioni e, in connessione con quanto le precede, le osservazioni che da esse si possono trarre.
- Equazione d'onda sferica
- Interferenza di due onde armoniche sferiche
- Parentesi matematica
- Conseguenze fisiche e significati
- Sorgenti in fase e di uguale intensità
- Simulazione con Mathematica
- Simulazione con GeoGebra
- Esperienza
Equazione d'onda sferica
L'equazione che descrive un'onda armonica piana che si propaga nella direzione positiva dell'asse \(x\) di un sistema cartesiano (onda progressiva) è espressa dalla funzione in due variabili
\[
y(x,t)=A \cos(\omega t-kx)
\]
con la costante \(A\) che rappresenta l'ampiezza, \(k\) il numero d'onda collegato alla lunghezza d'onda \(\lambda\) dalla relazione \(k=2\pi/\lambda\) e \(\omega\) la pulsazione, a sua volta legata alla frequenza \(f\) dalla \(\omega=2\pi
f\). Se le sorgenti emettono onde in tutte le direzioni e quindi, nel caso più semplice i fronti d'onda, ossia il luogo dei punti aventi la stessa fase ad un dato istante, sono superfici
sferiche, la precedente si estende alla
\begin{equation}
y(r,t)=A(r) \cos(\omega t-kr) \label{eq:eq01}
\end{equation}
essendo \(r\) la distanza dalla sorgente supposta puntiforme e \(A(r)\) una sua funzione. Al fine di determinare \(A(r)\) dobbiamo discutere quale sia la distribuzione spaziale dell'energia emessa dalla sorgente per cui, se \(P\) è
il valore medio dell'energia emessa per unità di tempo (o potenza) che caratterizza una data sorgente, l'intensità \(I\) rilevata su una superficie di area \(S\) e disposta perpendicolarmente alla direzione di
propagazione è data dal rapporto
\[
I=\frac{P}{S}.
\]
Per una sorgente puntiforme che emette onde in tutte le direzioni in un mezzo isotropo la potenza emessa deve distribuirsi uniformemente su fronti d'onda sferici di area \(4\pi r^2\) per cui, a distanza \(r\) dalla sorgente, la precedente
relazione si specifica nella
\begin{equation}
I=\frac{P}{4\pi r^2} \label{eq:eq02}
\end{equation}
e dato che \(P\) è una caratteristica intrinseca della sorgente, il prodotto \(4\pi r^2\cdot I=P\) dev'essere indipendente dalla distanza \(r\).
D'altra parte l'intensità di un'onda è proporzionale al quadrato della
sua ampiezza,
\begin{equation}
I\propto A^2 \qquad\hbox{ossia}\qquad I=c A^2 \label{eq:eq03}
\end{equation}
per cui dalla \(4\pi r^2\cdot I=P\) segue che
\begin{equation}
4\pi r^2\cdot c A^2=P \qquad\Longrightarrow\qquad r^2\cdot A^2=\frac{P}{4\pi c}.\label{eq:eq04}
\end{equation}
Osservata l'indipendenza da \(r\) del secondo membro, la dipendenza di \(A\) da \(r\), cioè la funzione \(A(r)\), dev'essere del tipo
\begin{equation}
A(r)=\frac{\hbox{costante}}{r} \label{eq:eq05}
\end{equation}
ossia l'ampiezza di un'onda sferica dev'essere inversamente proporzionale alla distanza dalla sorgente.
Ripresa quindi la \eqref{eq:eq01} e posto nella precedente \(\hbox{costante}=A\), un'onda armonica monocromatica emessa da una sorgente puntiforme caratterizzata da fronti d'onda sferici in uno spazio tridimensionale isotropo è
descritta dalla funzione
\begin{equation}
y(r,t)=\frac{A}{r}\cos(\omega t-k r)
\end{equation}
se la sua fase iniziale si suppone nulla quando \(r=0\) e \(t=0\) altrimenti, e più in generale, l'onda viene descritta dalla
\begin{equation}
y(r,t)=\frac{A}{r}\cos(\omega t-k r+\phi). \label{eq:eq07}
\end{equation}
con \(\phi\) fase iniziale.
Nota: se l'energia emessa da una sorgente si distribuisce anziché su una superficie sferica su un cilindro con raggio di base \(r\), l'ampiezza \(A(r)\) di tale onda dipende dalla distanza come \(A(r)=A/\sqrt{r}\). In tal caso si
tratta di onde cilindriche quali sono, per esempio, quelle emesse da una fenditura.
Interferenza di due onde armoniche sferiche
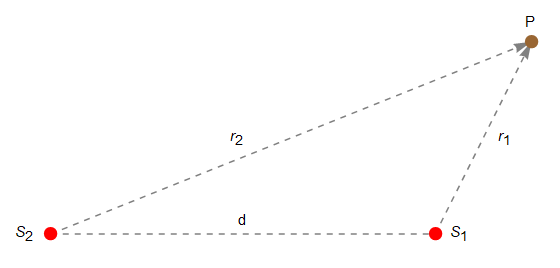
Consideriamo due sorgenti \(S_1\), \(S_2\) monocromatiche di onde sferiche poste alla reciproca distanza \(d\) e tali da mantenere costante nel tempo la loro differenza di fase. Se \(P\) è un punto individuato dai vettori posizione \(\vec{r}_1\) e \(\vec{r}_2\) relativamente a \(S_1\) e \(S_2\) (figura 1) , per quanto espresso dalla \eqref{eq:eq07} le onde emesse da tali sorgenti sono in \(P\) descritte dalle funzioni \begin{equation} y_1(r_1,t)=\frac{A_1}{r_1}\cos(\omega t-k r_1+\phi_1),\qquad y_2(r_2,t)=\frac{A_2}{r_2}\cos(\omega t-k r_2+\phi_2). \label{eq:eq08} \end{equation}
Per il principio di sovrapposizione l'onda risultante nel punto \(P\) è data dalla loro somma
\begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{
y(P)=y_1(r_1,t)+y_2(r_2,t)=\frac{A_1}{r_1}\cos(\omega t-k r_1+\phi_1)+\frac{A_2}{r_2}\cos(\omega t-k r_2+\phi_2),} \label{eq:eq09}
\end{equation}
mentre la loro differenza di fase \(\Delta\phi\) in \(P\) è
\begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{
\Delta\phi=(\omega t-k r_1+\phi_1)-(\omega t-kr_2+\phi_2)=-k(r_1-r_2)+(\phi_1-\phi_2)
}\label{eq:eq10}
\end{equation}
manifestamente indipendente dal tempo \(t\) appunto per la imposta coerenza delle due sorgenti.
Volendo comunque ottenere la distribuzione dell'intensità che, per la \eqref{eq:eq03} è proporzionale al quadrato dell'ampiezza, dovremo considerare la grandezza \(y^2(P)\) cioè
\begin{equation}
y^2(P)=\Biggl[\frac{A_1}{r_1}\cos(\omega t-k r_1+\phi_1)+\frac{A_2}{r_2}\cos(\omega t-k r_2+\phi_2)\biggr]^2. \label{eq:eq11}
\end{equation}
e quindi calcolarne il valor medio \(\overline{y^2(P)}\) esteso in un intervallo pari ad un periodo \(T\) tramite l'integrale
\begin{equation}
\overline{y^2(P)}=\frac{1}{T}\!\int_0^{T}\!\!y^2(P)\,{\rm d}t \label{eq:eq12}
\end{equation}
essendo \(y^2(P)\) una grandezza caratterizzata da tale periodicità.
A tal fine svolgiamo il quadrato di \eqref{eq:eq11} ottenendo
\begin{equation}
y^2(P)=\frac{A_1^2}{r_1^2}\cos^2(\omega t-k r_1+\phi_1)+\frac{A_2^2}{r_2^2}\cos^2(\omega t-k r_2+\phi_2)+2\frac{A_1A_2}{r_1r_2}\cos(\omega t-k r_1+\phi_1)\cos(\omega t-k r_2+\phi_2). \label{eq:eq13}
\end{equation}
per cui, per risolvere l'integrale \eqref{eq:eq12}, dovremo calcolare gli integrali
\begin{equation}
\frac{A_1^2}{r_1^2}\!\int_0^T\kern-3pt\cos^2(\omega t-k r_1+\phi_1)\,{\rm d}t,\qquad \frac{A_2^2}{r_2^2}\!\int_0^T\kern-3pt\cos^2(\omega t-k r_2+\phi_2)\,{\rm d}t. \label{eq:eq14}
\end{equation}
entrambi riconducibili alla forma
\begin{equation}
\int\!\cos^2(\omega t+\alpha)\,{\rm d}t \label{eq:eq15}
\end{equation}
e l'integrale
\begin{equation}
2\frac{A_1A_2}{r_1r_2}\int_0^T\kern-3pt\cos(\omega t-k r_1+\phi_1)\cos(\omega t-k r_2+\phi_2)\,{\rm d}t \label{eq:eq16}
\end{equation}
riconducibile alla forma
\begin{equation}
\int\!\cos(\omega t+\alpha)\cos(\omega t+\beta)\,{\rm d}t. \label{eq:eq17}
\end{equation}
Parentesi matematica
In questa sezione, a prevalente carattere matematico, procediamo al calcolo esplicito degli integrali indefiniti \eqref{eq:eq15} e \eqref{eq:eq17} e, conseguentemente ai corrispondenti valori medi \eqref{eq:eq14} e \eqref{eq:eq16}. Pertanto
utilizzando l'identità goniometrica
\begin{equation}
\cos^2\gamma =\frac{1+\cos(2\gamma)}{2} \label{eq:eq18}
\end{equation}
l'integrale \eqref{eq:eq15} si riscrive come
\[
\int\!\frac{1+\cos(2\omega t+2\alpha)}{2}\,{\rm d}t
\]
che si può quindi suddividere in
\[
\frac{1}{2}\!\int\!{\rm d}t+\frac{1}{2}\!\int\!\cos(2\omega t+2\alpha)\,{\rm d}t.
\]
Posto \(z=2\omega t+2\alpha\) per cui \({\rm d}z=2\omega {\rm d}t\) e quindi \({\rm d}t=(1/2\omega){\rm d}z\), possiamo ricondurre anche il secondo integrale ad uno elementare e risolvere
\begin{equation}
\frac{1}{2}\!\int\!{\rm d}t+\frac{1}{4\omega}\!\int\!\cos(z)\,{\rm d}z=\frac{t}{2} +\frac{1}{4\omega}\sin(z)=\frac{t}{2} +\frac{1}{4\omega}\sin(2\omega t+2\alpha).\label{eq:eq19}
\end{equation}
per cui, passando al calcolo degli integrali definiti, il primo delle \eqref{eq:eq14} si esplicita come
\begin{equation}
\frac{A_1^2}{r_1^2}\!\int_0^T\kern-3pt\cos^2(\omega t-k r_1+\phi_1)\,{\rm d}t= \frac{A_1^2}{r_1^2}\Biggl\{\frac{(T-0)}{2}+\frac{1}{4\omega}\bigl[\sin(2\omega T+2\phi_1-2kr_1)-\sin(2\phi_1-2k r_1)\bigr]\Biggr\},
\end{equation}
e tenendo presente che \(T=2\pi/\omega\) e la periodicità della funzione seno, il secondo addendo entro parentesi vale
\[
\sin(2\omega T+2\phi_1-2kr_1)-\sin(2\phi_1-2kr_1)=\sin(4\pi+2\phi_1-kr_1)-\sin(2\phi_1-2kr_1)=0,
\]
per cui risulta
\begin{equation}
\frac{A_1^2}{r_1^2}\!\int_0^T\kern-3pt\cos^2(\omega t-k r_1+\phi_1)\,{\rm d}t=\frac{A_1^2}{r_1^2}\cdot \Biggl(\frac{T}{2}+0\Biggr)=\frac{A_1^2}{r_1^2}\Biggl(\frac{1}{2}\cdot\frac{2\pi}{\omega}\Biggr)=\frac{A_1^2}{r_1^2}\cdot
\frac{\pi}{\omega}. \label{eq:eq20}
\end{equation}
Allo stesso modo il secondo integrale delle \eqref{eq:eq14} assume il valore
\begin{equation}
\frac{A_2^2}{r_2^2}\!\int_0^T\kern-3pt\cos^2(\omega t-k r_2+\phi_2)\,{\rm d}t=\frac{A_2^2}{r_2^2}\cdot \frac{\pi}{\omega}. \label{eq:eq21}
\end{equation}
Per quanto seguirà è utile sottolineare il valore nullo dell'integrale
\begin{equation}
\int_0^T\!\!\cos(2\omega t+2\alpha)\,{\rm d}t=0\label{eq:eq22}
\end{equation}
e coinvolto nel calcolo appena concluso.
Per risolvere l'integrale \eqref{eq:eq17} utilizziamo invece l'identità goniometrica di Werner
\[
\cos\gamma\cos\delta=\frac{1}{2}\bigl[\cos(\gamma+\delta)+\cos(\gamma-\delta)\bigr]
\]
che collega un prodotto con una somma di funzioni: in tal modo lo stesso integrale si riscrive come
\[
\int\!\cos(\omega t+\alpha)\cos(\omega t+\beta)\,{\rm d}t=\frac{1}{2}\!\int\Bigl[\cos(2\omega t+\alpha+\beta)+\cos(\alpha-\beta)\Bigr]{\rm d}t
\]
e si scompone in
\[
\int\!\cos(\omega t+\alpha)\cos(\omega t+\beta)\,{\rm d}t=\frac{1}{2}\!\int\cos(2\omega t+\alpha+\beta)\,{\rm d}t+\frac{1}{2}\cos(\alpha-\beta)\!\int\!{\rm d}t.
\]
Il valore dell'integrale definito \eqref{eq:eq16} è quindi
\begin{align}
2\frac{A_1A_2}{r_1r_2}&\!\int_0^T\kern-5pt\cos(\omega t-kr_1+\phi_1)\cos(\omega t-kr_2+\phi_2)\,{\rm d}t\label{eq:eq24}\\ &=2\frac{A_1A_2}{r_1r_2}\Biggl\{\frac{1}{2}\!\int_0^T\kern-4pt\cos\bigl[2\omega t-k(r_1+r_2)+(\phi_1+\phi_2)\bigr]{\rm
d}t+\frac{1}{2}\cos\bigl[-k(r_1-r_2)+(\phi_1-\phi_2)\bigr]\cdot (T-0)\Biggr\}\label{eq:eq25}
\end{align}
e considerando quanto detto circa il valore nullo del primo integrale entro parentesi, abbiamo in definitiva
\begin{align}
2\frac{A_1A_2}{r_1r_2}&\!\int_0^T\kern-3pt\cos(\omega t-kr_1+\phi_1)\cos(\omega t-kr_2+\phi_2)\,{\rm d}t\label{eq:eq26}\\ &= 2\frac{A_1A_2}{r_1r_2}\cdot \frac{T}{2}\cdot
\cos\bigl[-k(r_1-r_2)+(\phi_1-\phi_2)\bigr]=2\frac{A_1A_2}{r_1r_2}\cdot \frac{\pi}{\omega}\cdot\cos\bigl[-k(r_1-r_2)+(\phi_1-\phi_2)\bigr].\label{eq:eq27}
\end{align}
Considerando i tre termini nei quali è stato suddiviso l'integrale \eqref{eq:eq12} e riaggregando i risultati di questa sezione, \eqref{eq:eq20}, \eqref{eq:eq21}, \eqref{eq:eq27}, abbiamo che il valor medio del quadrato della
perturbazione risultante
\begin{align}
\overline{y^2(P)}=\frac{1}{T}\!\int_0^T\!y^2(P)\,{\rm d}t&=\frac{1}{T}\!\Biggl\{\frac{A_1^2}{r_1^2}\cdot \frac{\pi}{\omega}+\frac{A_2^2}{r_2^2}\cdot \frac{\pi}{\omega}+2\frac{A_1A_2}{r_1r_2}\cdot
\frac{\pi}{\omega}\cdot\cos\bigl[-k(r_1-r_2)+(\phi_1-\phi_2)\bigr]\Biggr\} \label{eq:eq28}\\
&= \frac{1}{2}\Biggl(\frac{A_1^2}{r_1^2}+\frac{A_2^2}{r_2^2}+\frac{2A_1 A_2}{r_1 r_2}\cos\Delta\phi \Biggr) \label{eq:eq29}
\end{align}
dove nell'ultima espressione si è utilizzata la posizione \eqref{eq:eq10}. Ripresa la \eqref{eq:eq03}, abbiamo pertanto che l'intensità risultante \(I\) è proporzionale al risultato \eqref{eq:eq29}
\begin{align}
I\propto \overline{y^2(P)}\quad\Longrightarrow\quad I= c\, \Biggl(\frac{A_1^2}{r_1^2}+\frac{A_2^2}{r_2^2}+\frac{2A_1 A_2}{r_1 r_2}\cos\Delta\phi \Biggr) \label{eq:eq30}
\end{align}
e osservato come le intensità delle singole sorgenti siano, in \(P\), pari a
\begin{equation}
I_1=c\, \frac{A_1^2}{r_1^2}\qquad I_2=c\, \frac{A_2^2}{r_2^2}, \label{eq:eq31}
\end{equation}
l'intensità complessiva \(I\) in termini delle intensità delle singole onde emesse è in definitiva
\begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{
I=I_1+I_2+2\sqrt{I_1 I_2}\cos\Delta\phi} \label{eq:eq32}
\end{equation}
Conseguenze fisiche e significati
Il principale significato che discende dal risultato \eqref{eq:eq32} consiste nell'osservare come l'intensità totale in un punto non sia la semplice somma delle singole intensità ma che la relazione sia invece più
complessa. Pertanto l'ambito di validità del principio di sovrapposizione dei fenomeni ondulatori è circoscritto alle sole grandezze rappresentate dalla funzione \(y\) quali possono essere, per esempio, la pressione per le
onde sonore oppure il campo elettrico e/o magnetico per le onde elettromagnetiche e/o la luce, mentre tale principio non è applicabile alle associate intensità e ciò a causa del termine \(2\sqrt{I_1 I_2}\cos\Delta\phi\)
detto termine di interferenza.
Tale termine
\begin{equation}
2\sqrt{I_1 I_2}\cos\Delta\phi= 2\sqrt{I_1 I_2}\cos\bigl[-k(r_1-r_2)+(\phi_1-\phi_2)\bigr] \label{eq:eq33}
\end{equation}
dipende
- dalla differenza delle fasi iniziali \((\phi_1-\phi_2)\), grandezza indipendente dal punto \(P\) ma dipendente solo dalle due sorgenti e
- dal termine \(k(r_1-r_2)\) manifestamente funzione delle distanze di \(P\) dalle sorgenti.
Se quindi il coseno assume i valori estremi rispettivamente
\[
\cos\bigl[-k(r_1-r_2)+(\phi_1-\phi_2)\bigr]=+ 1
\]
cioè
\begin{equation}
-k(r_1-r_2)+(\phi_1-\phi_2)=+2n\pi,\qquad n=0, \pm 1, \pm 2,\ldots \label{eq:eq34}
\end{equation}
l'intensità risultante è massima
\begin{equation}
I_{max}=I_1+I_2+2\sqrt{I_1I_2}>I_1+I_2 \label{eq:eq35}
\end{equation}
e risulta maggiore di \(I_1+I_2\) mentre se
\[
\cos\bigl[-k(r_1-r_2)+(\phi_1-\phi_2)\bigr]=-1
\]
cioè
\begin{equation}
-k(r_1-r_2)+(\phi_1-\phi_2)=(2n+1)\pi,\quad n=0, \pm 1, \pm 2,\ldots \label{eq:eq36}
\end{equation}
l'intensità raggiunge il valore minimo
\begin{equation}
I_{min}=I_1+I_2-2\sqrt{I_1I_2} \label{eq:eq37}
\end{equation}
minore di \(I_1+I_2\). La condizione \eqref{eq:eq34} rappresenta perciò il caso dell'interferenza costruttiva dove la differenza di fase \(\Delta\phi\) è un multiplo pari di \(\pi\) mentre la \eqref{eq:eq36} esprime la
condizione per l'interferenza distruttiva con \(\Delta\phi={}\)multiplo dispari di \(\pi\).
La differenza tra le due intensità è data dalla
\begin{equation}
\Delta I=I_{max}-I_{min}=\bigl(I_1+I_2+2\sqrt{I_1I_2}\bigr)-\bigl(I_1+I_2-2\sqrt{I_1I_2}\bigr)=4\sqrt{I_1 I_2}. \label{eq:eq38}
\end{equation}
e, nel caso di onde luminose, tale ridistribuzione spaziale dell'energia dà origine ad un sistema di frange di interferenza alternativamente più o meno chiare.
Nella figura 2 rappresentiamo quindi l'andamento dell'intensità \eqref{eq:eq32} in funzione della differenza di fase \(\Delta\phi\)
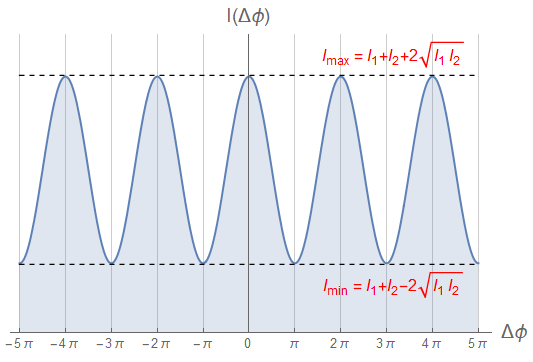
Sorgenti in fase e di uguale intensità
Il caso più interessante nell'interferenza di onde emesse da due sorgenti si presenta quando le due sorgenti sono in fase ossia quando, in riferimento alle \eqref{eq:eq08}, \(\phi_1=\phi_2\) (o più in generale
\(\phi_1-\phi_2=2n\pi\)). In tal caso la differenza di fase dell'onda risultante rappresentata dalla \eqref{eq:eq10} dipende solo dal punto \(P\)
\begin{equation}
\Delta\phi=k|r_1-r_2| \label{eq:eq39}
\end{equation}
(consideriamo il valore assoluto della differenza \(r_1-r_2\)), e le condizioni di interferenza costruttiva e distruttiva si semplificano nelle
\[
k\,|r_1-r_2|= 2n\pi,\hskip2cm k\,|r_1-r_2|= (2n+1)\pi
\]
per cui, introdotta la relazione tra il numero d'onda \(k\) e la lunghezza d'onda \(\lambda\), \(k=2\pi/\lambda\), si riducono alle
\begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{
|r_1-r_2|= n\lambda=2n\Bigl(\frac{\lambda}{2}\Bigr),\hskip2cm |r_1-r_2|= (2n+1)\Bigl(\frac{\lambda}{2}\Bigr).} \label{eq:eq40}
\end{equation}
Se ci limitiamo a considerare il punto \(P\) appartenente ad un piano contenente le due sorgenti, le ultime due relazioni definiscono, al variare di \(n\) due famiglie discrete di iperboli aventi i
fuochi in \(S_1\) e \(S_2\). Difatti, data la costanza della lunghezza d'onda (le due sorgenti sono, per ipotesi, monocromatiche) e fissato l'indice \(n\), il secondo membro delle \eqref{eq:eq40} è una costante e così queste
relazioni rientrano nella classica definizione dell'iperbole quale luogo di punti tali da avere costante il valore assoluto della differenza delle distanze da due punti fissi, i fuochi dell'iperbole.
Se poi le due sorgenti possiedono pure la medesima ampiezza cioè \(A_1=A_2\) e i percorsi seguiti sono circa uguali \(r_1\approx r_2\) cosicché
\begin{equation}
A_1=A_2,\quad r_1\approx r_2 \quad \Longrightarrow \quad \frac{A_1^2}{r_1^2}\approx \frac{A_2^2}{r_2^2} \label{eq:eq41}
\end{equation}
ne discende per \eqref{eq:eq31} l'uguaglianza approssimata tra le intensità \(I_1\approx I_2\) per cui i valori estremi \(I_{max}\) e \(I_{min}\) espressi rispettivamente dalle \eqref{eq:eq35} e \eqref{eq:eq37} assumono in tale
limite i valori
\begin{equation}
I_{max}=2I_1+2\sqrt{I_1^2}=4I_1\hskip2cm I_{min}=2I_1-2I_1=0. \label{eq:eq42}
\end{equation}
Sotto tali ipotesi, nell'interferenza distruttiva si può quindi giungere all'estinzione completa della perturbazione (come dire, simpaticamente, luce + luce = buio!) mentre in quella costruttiva l'intensità raggiunta
è pari a 4 volte l'intensità dovuta ad una singola sorgente nel medesimo punto.
Se definiamo come visibilità il rapporto
\begin{equation}
v=\frac{I_{max}-I_{min}}{I_{max}+I_{min}}=\frac{4\sqrt{I_1 I_2}}{2(I_1+I_2)}=\frac{2\sqrt{I_1 I_2}}{I_1+I_2}
\end{equation}
e osservato che \(0≤v≤1\), nel caso di ampiezze uguali e per le \eqref{eq:eq42}, tale grandezza assume il valore massimo
\begin{equation}
v=\frac{2I_1}{2I_1}=1
\end{equation}
mentre nel caso di ampiezze via via diverse è immediato dimostrare che \(v< 1\) cosicché le differenze in intensità tra massimi e minimi diventano meno rilevanti e, nel caso di onde luminose, ciò si accompagna
ad una diminuzione del contrasto. Questo fatto dà ragione della ricerca nelle esperienze di interferometria di far interagire fasci aventi la medesima intensità così da ottenere, almeno nell'interferenza luminosa, un
sistema di frange costituito da una successione di frange chiare e scure e dal massimo contrasto.
Se l'interazione avviene tra onde piane aventi la medesima ampiezza e per le quali l'intensità non dipende dalla distanza dalle sorgenti, allora le condizioni approssimate \eqref{eq:eq41} sono soddisfatte
esattamente per cui posto \(I_1=I_2=I_0\), la relazione \eqref{eq:eq32} si riduce alla
\begin{equation}
I=2I_0+2I_0\cos\Delta\phi=2I_0(1+\cos\Delta\phi)
\end{equation}
e con l'identità goniometrica già utilizzata in \eqref{eq:eq18}
\[
1+\cos(\alpha)=2\cos^2\Bigl(\frac{\alpha}{2}\Bigr)
\]
la distribuzione in intensità dell'interferenza di due onde piane prodotte da sorgenti in fase e monocromatiche viene rappresentata in termini della differenza di fase dalla funzione
\[
I=4I_0\cos^2\Bigl(\frac{\Delta\phi}{2}\Bigr)
\]
oppure, con le \eqref{eq:eq39},
\begin{equation}
I=4I_0\cos^2\Bigl[\frac{k}{2}(r_1-r_2)\Bigr]=4I_0\cos^2\Bigl[\frac{\pi}{\lambda}(r_1-r_2)\Bigr]. \label{eq:eq46}
\end{equation}
Tale distribuzione si presenta nello studio dell'interferenza di due onde piane nella classica esperienza di Thomas Young nel 1801 dove, seppure i fronti d'onda prodotti siano sferici o, più correttamente, cilindrici quando le due
"sorgenti" siano rappresentate da due fenditure, la grande distanza rispetto alla separazione delle sorgenti garantisce che tali fronti d'onda siano assimilabili a dei piani e quindi con una distribuzione in intensità coerente con la
\eqref{eq:eq46}. Come descritto in molti testi e nella pagina seguente, se \(L\) è la distanza tra le fenditure e lo schermo, \(d\) la separazione delle fenditure e \(y\) la posizione di un
punto \(P\) sullo schermo, la stima della differenza di percorso \(r_1-r_2\) è
\begin{equation}
r_1-r_2=\frac{d\,y}{L}
\end{equation}
per cui la \eqref{eq:eq46} diviene
\begin{equation}
I=4I_0\cos^2\Bigl[\frac{\pi\,d\,y}{\lambda L}\Bigr] \label{eq:eq48}
\end{equation}
funzione che in figura 3 rappresentiamo in termini di multipli della distanza \(\lambda L/2d\) cioè pari a mezzo periodo.
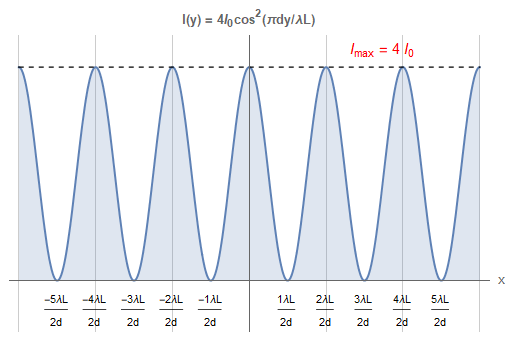
Se \[ m\pi=\frac{\pi d\,y_{m}}{\lambda L},\hskip1cm (m+1)\pi=\frac{\pi d\,y_{m+1}}{\lambda L} \] sono gli angoli rispettivamente di ordine \(m\) e \(m+1\) in corrispondenza dei quali l'intensità raggiunge il valore massimo (o minimo) e definita la separazione \(\Delta y=y_{m+1}-y_{m}\) tra due successivi massimi (o minimi) misurata sullo schermo, discende che \begin{equation} (m+1)\pi-m\pi=\frac{\pi d\,y_{m+1}}{\lambda L}-\frac{\pi d\,y_{m}}{\lambda L}\quad\Longrightarrow\quad \pi=\frac{\pi\,d\,\Delta y}{\lambda L} \label{eq:eq49} \end{equation} da cui otteniamo per la lunghezza d'onda l'espressione \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{ \lambda =\frac{d\,\Delta y}{L}} \label{eq:eq50} \end{equation} tramite la quale si potrà stimare la lunghezza d'onda in termini di grandezze misurabili in laboratorio (v. pagina seguente).
Simulazione con Mathematica
La "Demonstration" che qui presentiamo è pubblicata all'indirizzo demonstrations.wolfram.com ed è prelevabile sia nel
formato NB di Mathematica (Author Code) che nel formato CDF utilizzabile in modo interattivo se nel proprio sistema è installato il gratuito Wolfram Player.
Questa permette di simulare la distribuzione dell'intensità dovuta all'interferenza di due sorgenti monocromatiche e in fase al variare di parametri quali la loro lunghezza d'onda, separazione spaziale e distanza dalle sorgenti. Di
seguito, a ciascuna immagine associamo le principali osservazioni che da essa si possono trarre e i collegamenti con la precedente parte teorica.
Figura 4
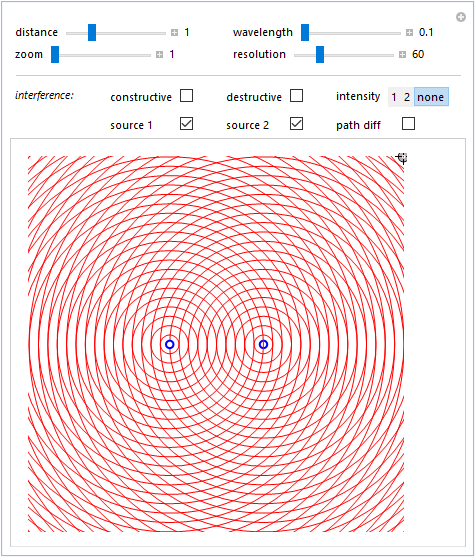
Nella figura 4 sono rappresentati geometricamente i fronti d'onda emessi dalle due sorgenti ossia quei punti che, in un dato istante, sono caratterizzati dalla stessa fase o, se appartenente ad un diverso fronte d'onda, da una fase che differisce per un multiplo di \(2\pi\). È evidente che tali fronti d'onda sono delle circonferenze concentriche a ciascuna sorgente e la differenza tra la lunghezza del raggio di ciascuna con quella precedente (o successiva) è pari ad una lunghezza d'onda. Difatti in base alla \eqref{eq:eq07}, se \[ \Delta\phi=\bigl|(\omega t-kr_2+\phi)-(\omega t-kr_1+\phi)\bigr|=k|r_2-r_1|=2\pi, \] segue che \[ \frac{2\pi}{\lambda}\cdot |r_2-r_1|=2\pi\quad\Longrightarrow\quad |r_2-r_1|=\lambda. \] I punti di intersezione tra le due distinte famiglie di circonferenze suggeriscono inoltre le linee di interferenza costruttiva.
Figura 5
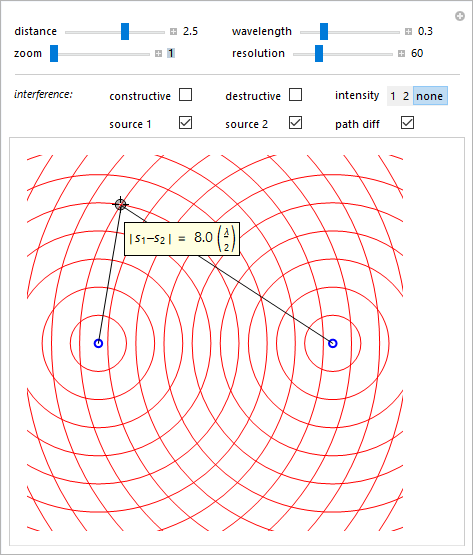
Si è modificata la lunghezza d'onda e la distanza tra le sorgenti e trascinato il selettore ("locator"), inizialmente posto nel centro dell'immagine, nel punto di intersezione tra due fronti d'onda. Come evidenziato dall'etichetta associata, la distanza di tale punto dalla prima sorgente è pari a \(9\lambda\) mentre dalla seconda è di \(5\lambda\). La differenza di cammino è quindi \(r_1-r_2=4\lambda=8(\lambda/2)\) coerentemente con la prima condizione \eqref{eq:eq40} per cui in tale punto le onde interferiscono costruttivamente.
Figura 6
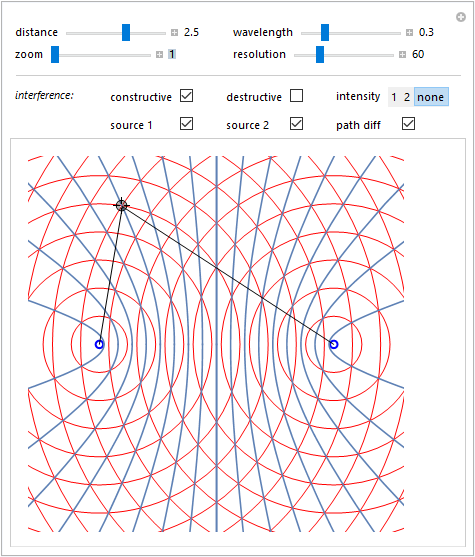
Alla precedente si sono aggiunte le linee di interferenza costruttiva caratterizzate da punti aventi il valore assoluto della differenza di distanza dalle sorgenti pari ad un multiplo della lunghezza d'onda. Tali linee sono delle iperboli aventi i fuochi sulle sorgenti: per la loro codifica matematica si è sfruttata la rappresentazione parametrica data dalla coppia di equazioni \[ \cases{x=a \sec t\\ y=b\tan t} \] con \(a= n\lambda/2\) e \(b=\sqrt{c^2-a^2}\) essendo \(c\) l'ascissa che sintetizza la posizione sull'asse \(x\) dei fuochi ed \(n=2,4,\dots\) un intero pari.
Figura 7
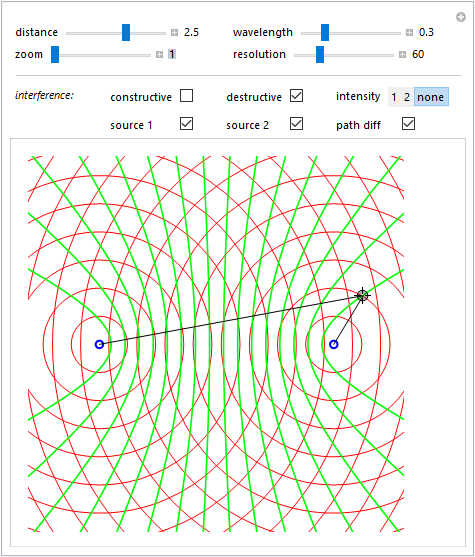
Sono ora evidenziate le linee di interferenza distruttiva \eqref{eq:eq40} e il locator è posizionato su quella caratterizzata da una differenza di distanza dalle sorgenti pari a \(15\lambda/2\).
Figura 8
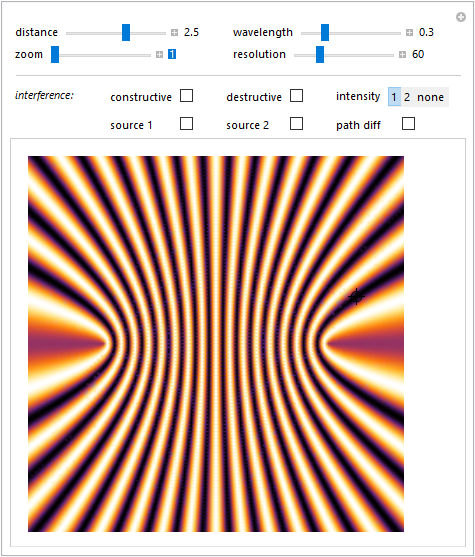
La scelta di intensity 1 mostra la distribuzione in intensità dell'interferenza tra le onde emesse da \(S_1\) e \(S_2\) supponendo che la loro ampiezza sia costante e quindi indipendente dalla distanza dalle sorgenti siano cioè rappresentate da onde piane. La distribuzione segue quindi la funzione \eqref{eq:eq46} \[ I=4I_0\cos^2\Bigl[\frac{\pi}{\lambda}(r_1-r_2)\Bigr]. \]
Figura 9
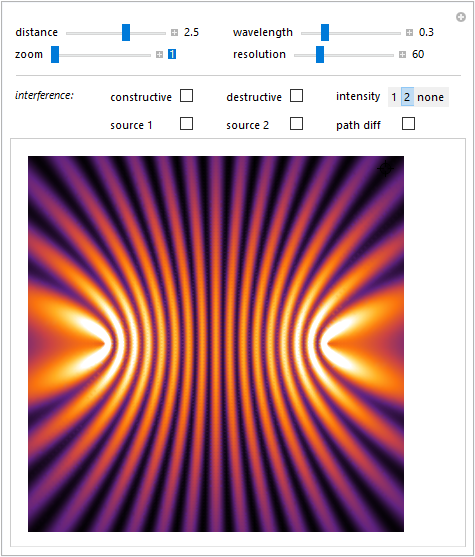
Più realisticamente selezionando intensity 2, viene riportata la distribuzione in intensità supponendo che l'ampiezza delle onde che interferiscono dipenda in modo inverso dalla distanza dalle sorgenti. Le onde sono quindi supposte sferiche e le corrispondenti intensità diminuiscono con l'inverso del quadrato della distanza secondo quanto espresso dalla relazione \eqref{eq:eq30} \[ I= c\, \Biggl(\frac{A_1^2}{r_1^2}+\frac{A_2^2}{r_2^2}+\frac{2A_1 A_2}{r_1 r_2}\cos\Delta\phi \Biggr)\quad\hbox{con}\quad \Delta\phi=\frac{2\pi}{\lambda}|r_1-r_2|. \]
Simulazione con GeoGebra
Osservazioni analoghe a quelle discusse nei riquadri delle figure 4, 5, 6 e 7 si possono fare sulla base del file di GeoGebra distribuito di seguito.
Esperienza
Per un'esperienza sull'interferenza che riproduca, in alcuni aspetti, la storica esperienza di T. Young si veda la pagina successiva.