Esperienze di fisica
Esempi di utilizzo didattico della regressione
L'analisi di regressione trova fondamentali applicazioni e significative conferme là dove la si impiega nelle diverse problematiche concrete del mondo reale e, in ambito didattico, appare particolarmente utile in laboratorio dove offre l'occasione di integrare gli aspetti pratici del processo di misura con quelli di una sua elaborazione con mezzi informatici. Alla precedente trattazione teorica sulla regressione associamo quindi nella prima parte di questa seconda pagina alcuni esempi didattici introduttivi utilizzando un software molto diffuso qual è GeoGebra e, in parallelo, proponiamo semplici ma indicativi notebook di Jupyter scritti nel linguaggio Python. Nella seconda parte e al solo scopo di fornire utili spunti, applichiamo invece i metodi della regressione ad esperienze svolte in un laboratorio didattico.
In ogni sezione riportiamo i risultati con delle figure che comunque rimandano, come link, ai rispettivi file di origine. In alternativa gli stessi file sono ripresi nell'elenco al termine di ciascuna presentazione mentre il repository complessivo GitHub è raggiungibile con il link https://github.com/lrnzr/regressione dove i notebook si potranno, oltreché consultare, avviare in forma interattiva.
PARTE 1. Esempi didattici
PARTE 2. Esperienze di laboratorio
- Prima legge di Ohm
- Seconda legge di Ohm
- Seconda legge di Gay-Lussac
- Moto uniformemente accelerato
- Esperienza di Fletcher
- Legge di Boyle
- Scarica di un condensatore su resistore
- Legge di Snell della rifrazione
- Regressione circolare: diffrazione di Fraunhofer
- Traiettoria circolare di elettroni in campo magnetico
- Simulazione della regressione circolare
- Dalla poligonale al poligono regolare
PARTE 1. Esempi didattici
Esempio 1
Per un primo approccio alla regressione lineare proponiamo
- il file di GeoGebra esempio1.ggb prelevabile con un clic sulla figura 1 o dalla tabella sottostante come
- il notebook di Jupyter esempio1.ipynb pure consultabile come pagina HTML al link esempio1.html.

Il file di GeoGebra permette di muovere in modo interattivo 5 punti e nello stesso tempo ottenere la retta di regressione e la sua equazione. La pendenza \(a\) e l'intercetta \(b\) della retta di regressione vengono calcolati nella vista "foglio di calcolo" coinvolgendo gli elementi costitutivi delle formule (11) come riportate nella pagina di teoria.
Il notebook di Jupyter invece, chiede l'inserimento di un certo numero di coppie di valori nella forma [x,y] e quindi calcola pendenza e intercetta sfruttando, per il parametro \(a\), la prima delle formule (11) e, per \(b\), la seconda della (10).
Esempio 2
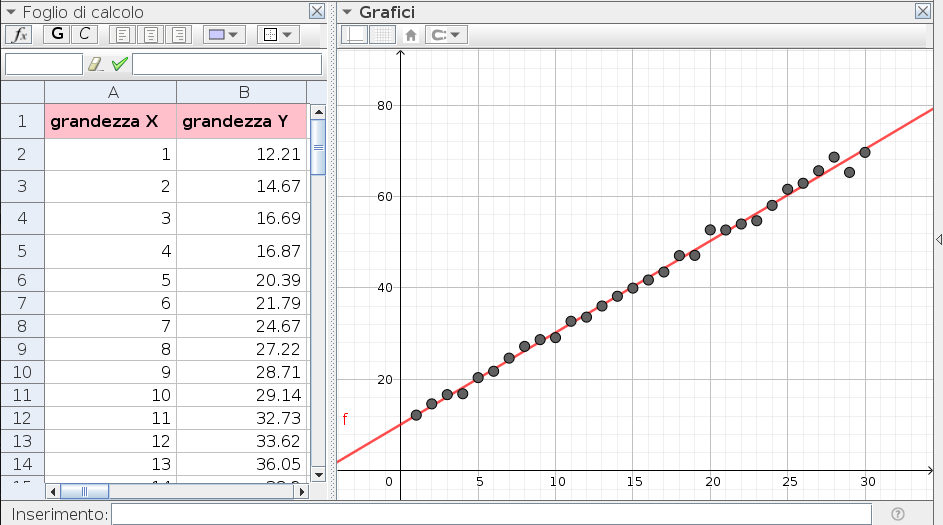
GeoGebra. Diversamente dal precedente, nel foglio di calcolo di GeoGebra vengono calcolate 30 coppie di valori. Le ordinate sono distribuite in modo casuale attorno ad una retta mentre le ascisse sono equispaziate e ordinate sequenzialmente al solo scopo di disporre di una più chiara rappresentazione grafica. Nulla cambia se pure le ascisse fossero distribuite casualmente. I parametri della retta di regressione vengono calcolati ancora sulla base delle formule (11) (fig. 2).
Volendo invece procedere con le voci di menu di GeoGebra, evidenziare la regione delle coppie di dati e quindi selezionare dal menu l'icona "Analisi di regressione bivariata". Nel caso la sorgente dei dati sia quella voluta, selezionare "Analizza" per ottenere, nella vista "Analisi dei dati" il grafico a dispersione. Dopo aver scelto il modello lineare di regressione, GeoGebra fornisce l'equazione della retta di regressione e la sua rappresentazione grafica. Le coppie rappresentative dei dati si possono infine riportare nella vista grafici per ulteriori elaborazioni.
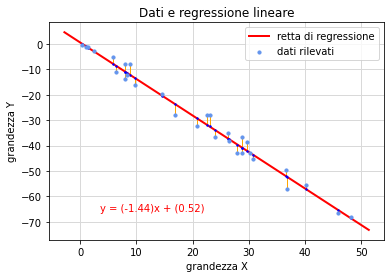
Jupyter. Il notebook esempio2.ipynb genera un insieme di 30 coppie di valori che simulano le misure sperimentali, le salva in un file nel formato CSV (per eventuale altra elaborazione) e quindi, in base alle stesse formule (11), fornisce a video i parametri della retta di regressione.
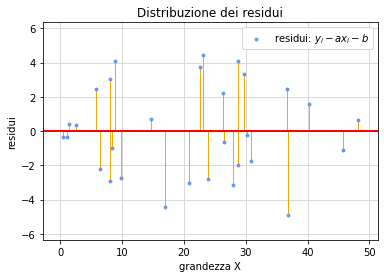
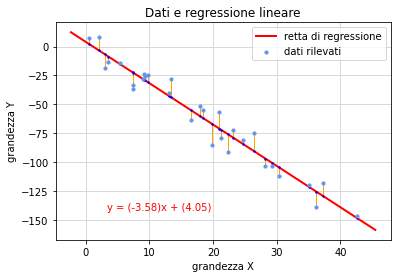
Jupyter (output grafico). Questo notebook esempio2-grafico.ipynb genera un insieme di 30 coppie di valori che simulano delle misure sperimentali e li rappresenta graficamente (fig. 3) assieme alla retta di regressione, alla sua equazione e ai segmenti indicativi dei residui.
Esempio 3
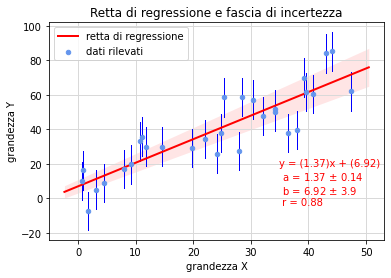
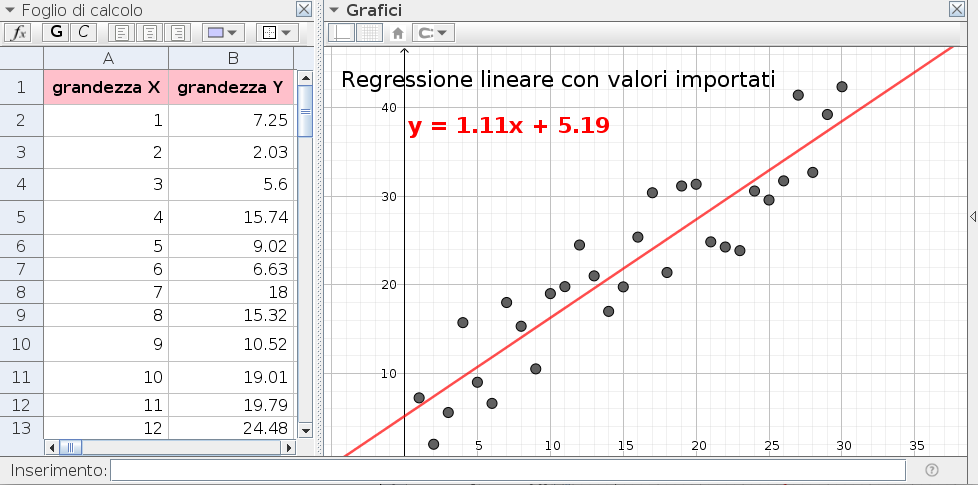
GeoGebra. Diversamente dai precedenti, l'insieme delle misure in esempio3.ggb viene importato da un file in formato CSV e quindi, in aggiunta ai parametri \(a\) e \(b\) caratterizzanti la retta di regressione si calcolano sulla base delle formule (31) e (32) e nella vista foglio, pure le loro incertezze \(\sigma_a\) e \(\sigma_b\) (fig. 4).
In aggiunta alla visualizzazione della dispersione delle misure è possibile ottenere pure quella dei residui. Difatti, ottenuto il grafico di dispersione dei dati nella finestra "Analisi dei dati", scelto il modello di regressione lineare, si può sostituire il grafico di dispersione con quello dei residui.
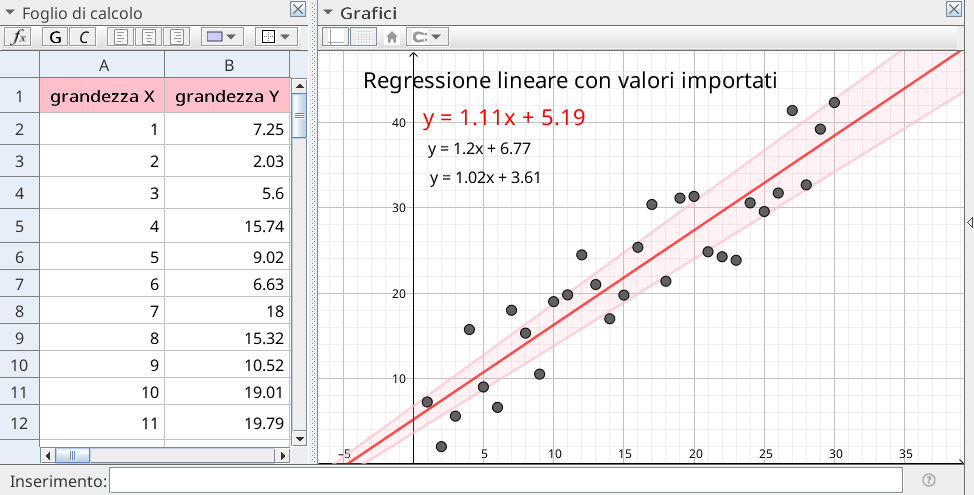
GeoGebra. In quest'altro file (esempio3-interne.ggb) si chiede come nel precedente la lettura dei dati da un file CSV e quindi, nella vista foglio di calcolo, si calcolano i parametri \(a,\,b,\,\sigma_a,\,\sigma_b\) e il coefficiente di correlazione \(r\) utilizzando le funzioni predefinite in GeoGebra (fig. 5).
Jupyter. Il notebook esempio3-grafico.ipynb legge i dati da un file (per es. dati02.csv) e calcola i parametri della retta di regressione. Visualizza quindi in un grafico i dati e la retta e in un secondo grafico la distribuzione dei residui (fig. 6).
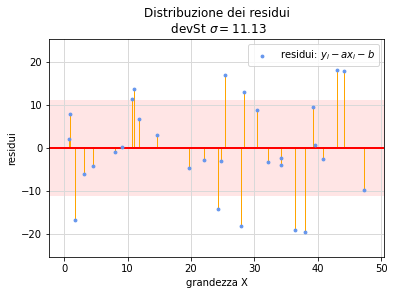
Jupyter. Il notebook esempio3-completo.ipynb aggiunge al precedente il calcolo della deviazione standard dei dati \(\sigma\) e delle incertezze \(\sigma_a,\,\sigma_b\) dei parametri (utilizzando le formule (31) e (32)). Rappresenta inoltre la fascia di incertezza della retta di regressione (fig. 7).
Esempio 4
Excel/Calc. Importato l'insieme di dati da un file CSV, il foglio di calcolo Excel/Calc esempio4.xlsx tramite le funzioni interne regressione(y_note;x_note), intercetta(y_note;x_note) e, soprattutto, reg.lin(), calcola tutti i parametri della regressione e riporta i grafici della dispersione dei dati e dei residui (fig. 8).
Jupyter. Il notebook esempio4-interne.ipynb esegue gli stessi calcoli del precedente esempio3-completo.ipynb ma utilizzando la funzione linregress della libreria SciPy, funzione che verrà utilizzata in buona parte dei notebook seguenti.
PARTE 2. Esperienze di laboratorio
Di seguito riportiamo alcune delle numerose applicazioni della regressione che si possono presentare in un laboratorio didattico. Di ognuna proponiamo alcune sintetiche osservazioni associandole alle immagini tratte dai file utilizzati per l'elaborazione (foglio di calcolo oppure notebook Jupyter). Volendo sperimentare in modo interattivo, i file CSV con i dati rilevati sono presenti nel repository https://github.com/lrnzr/regressione e il loro nome coincide con quello dell'esperienza.
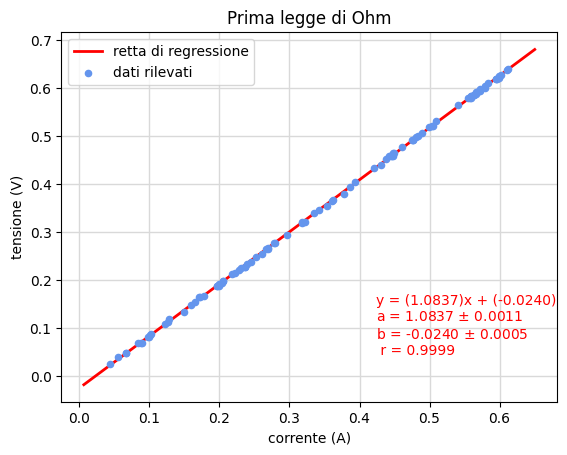
Prima legge di Ohm
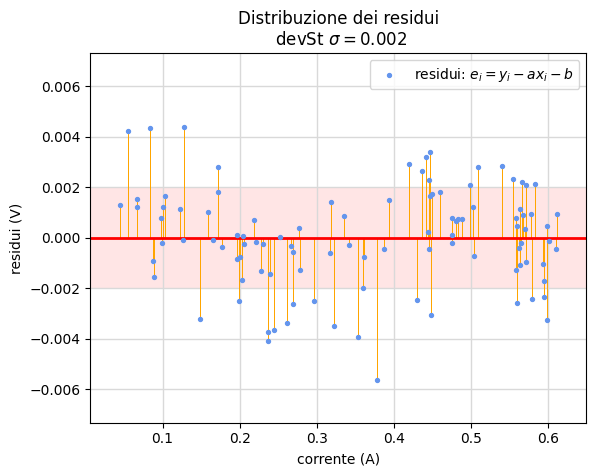
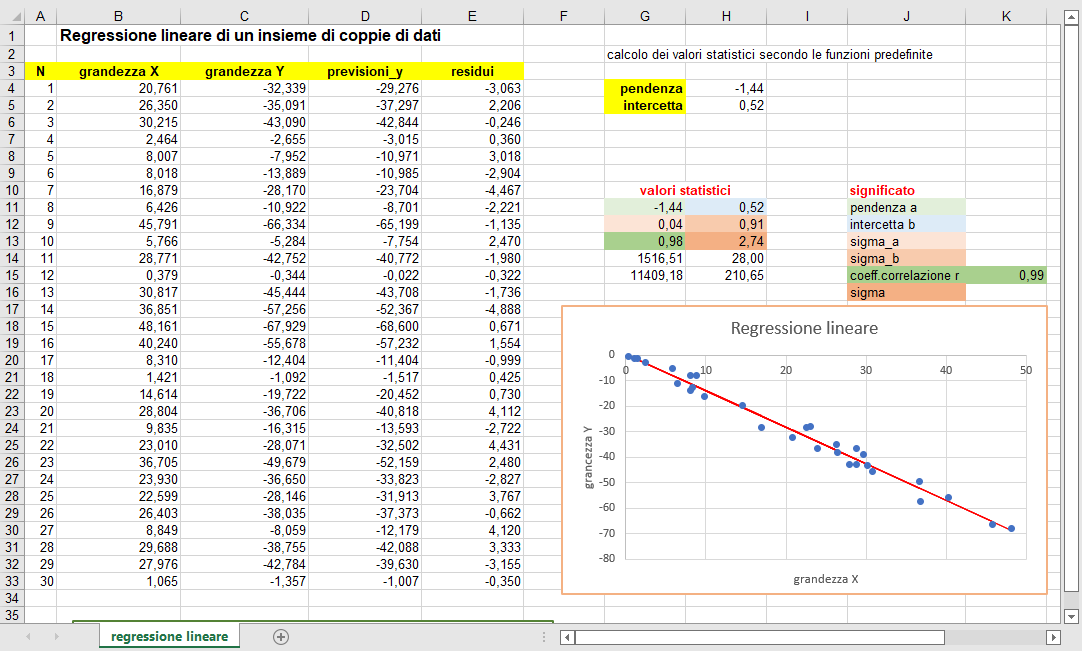
Le figure 9 e 10 riportano parte dell'elaborazione condotta per la verifica della prima legge di Ohm. Le 102 misure sono state acquisite variando arbitrariamente la tensione ai capi di un filo di costantana lungo 20 cm e di 0.35 mm di diametro.
Appare evidente la bontà delle misure in quanto la deviazione standard della resistenza \(\sigma_a=0.001\,\Omega\) è meno di un millesimo del valore della grandezza misurata \(R=1.084\,\Omega\).
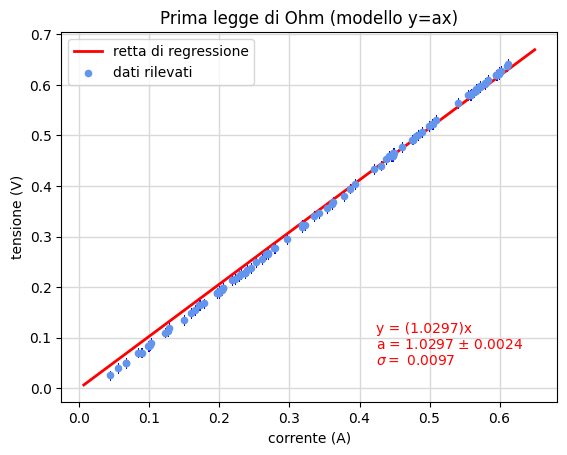
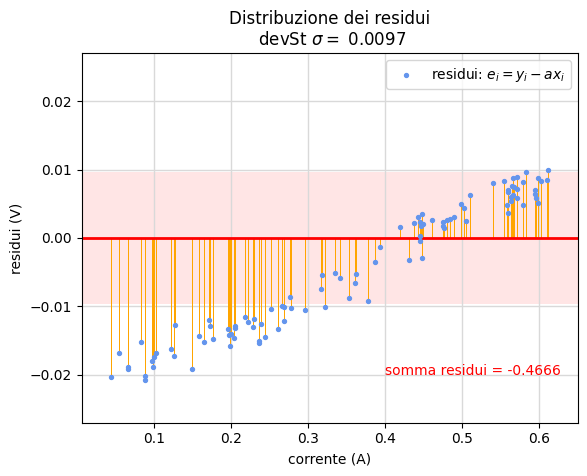
Nella successiva figura (fig. 10b) riportiamo i risultati ottenuti a partire dall'insieme di dati precedente ma nell'ipotesi che la relazione tra tensione e corrente sia di semplice proporzionalità (come in effetti è!). Le formule applicate sono quindi quelle collegate al modello descritto dall'equazione \(y=ax\).
Com'è facile osservare, il passaggio per l'origine della retta di regressione produce un sistematico disaccordo con la dispersione delle misure, disaccordo che appare più evidente nella distribuzione dei residui e nella loro deviazione standard che risulta ben 5 volte maggiore della corrispondente deviazione calcolata nel modello lineare completo (fig. 10). Inoltre, come accennato nella pagina di teoria, la somma dei residui non è nulla. Siccome situazioni analoghe si incontrano anche in contesti differenti (certamente dovute alle incertezze dei dati sperimentali e alla strumentazione utilizzata), nel seguito cercheremo sempre la retta di regressione associata al modello lineare completo descritto dall'equazione \(y=ax+b\) magari osservando, là dove sia opportuno, come si possa trascurare il termine noto \(b\) che in tal modo si ottiene.
Seconda legge di Ohm
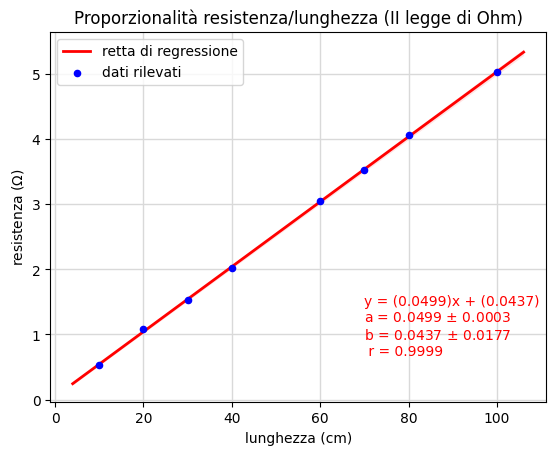
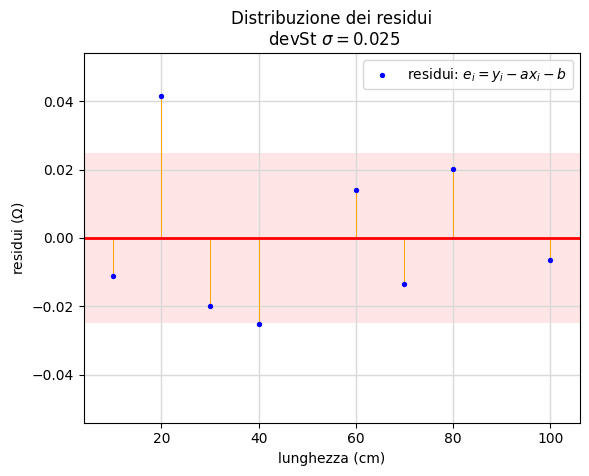
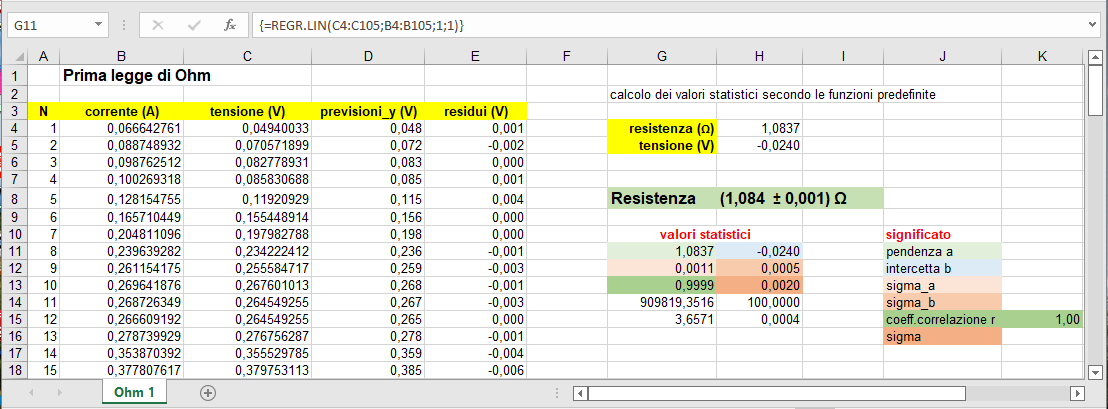
In questa seconda esperienza intendiamo verificare la proporzionalità della resistenza di un filo con la sua lunghezza cioè parte della seconda legge di Ohm. Ripetiamo quindi la procedura dell'esempio precedente per misurare con metodo volt-amperometrico la resistenza del filo ma, in questo caso, variandone la sua lunghezza. Le figure successive 11 e 12 dove la prova n. 2 coincide con quella discussa precedentemente, riassumono sinteticamente i risultati.
Ottenuto il coefficiente di proporzionalità tra resistenza e lunghezza e, supposta nota con altra esperienza la proporzionalità inversa con la sezione, è possibile risalire alla resistività ottenendo un valore del tutto compatibile con le aspettative (fig. 11).
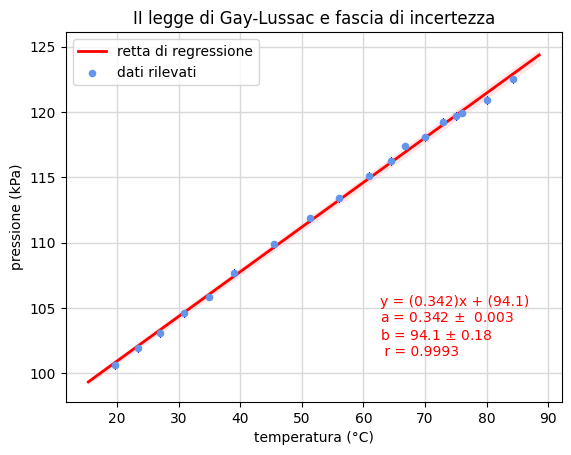
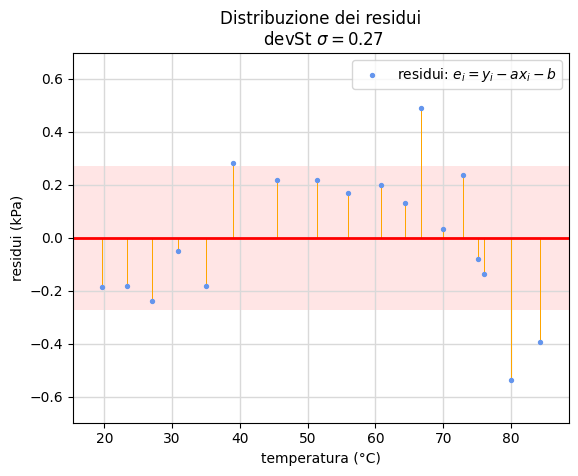
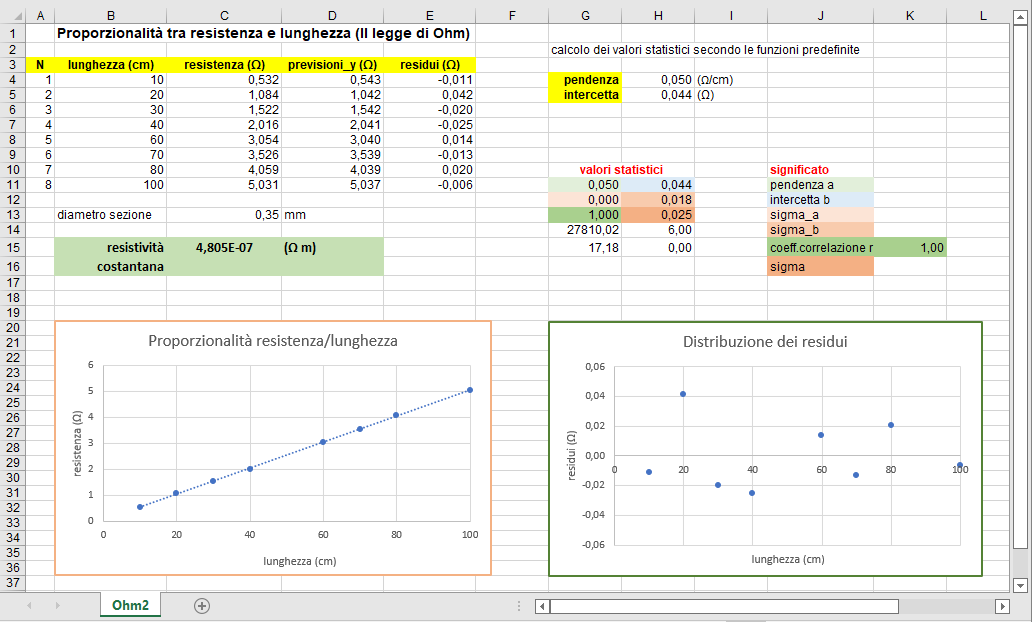
Seconda legge di Gay-Lussac
La seconda legge di Gay-Lussac lega linearmente la temperatura e la pressione di un gas. Le 16 coppie di misure riportate in figura 13 partono dai valori ambientali di temperatura e pressione per giungere alla temperatura di 85 °C e alla pressione di 122 kPa circa.
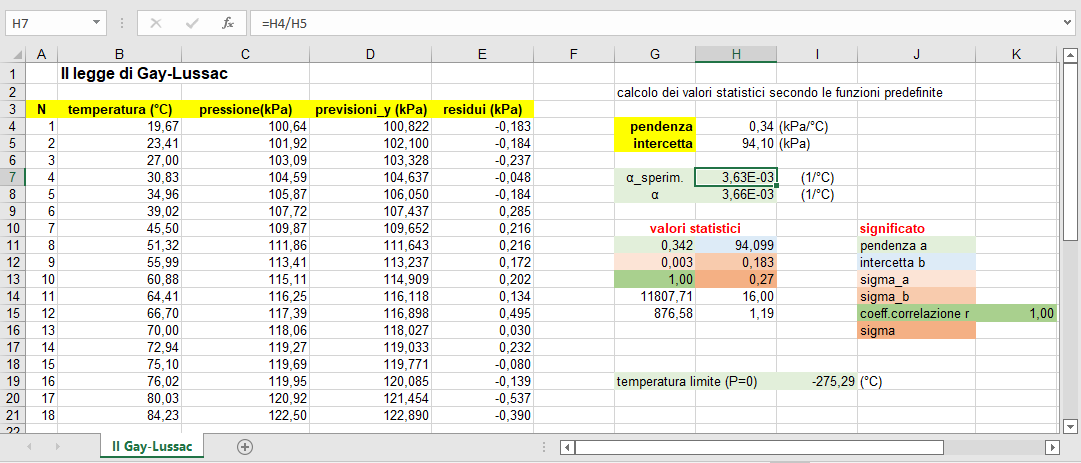
La pendenza della retta di regressione esprime il prodotto del coefficiente di dilatazione termica \(\alpha\) con la pressione standard \(p_0\). Identificata quest'ultima con la pressione ambientale (prossima a quella standard) si può quindi ottenere sperimentalmente il valore del coefficiente \(\alpha\). Inoltre, imponendo la condizione \(p=0\) nell'equazione della retta di regressione si giunge ad una stima della temperatura limite o zero Kelvin (fig. 13).
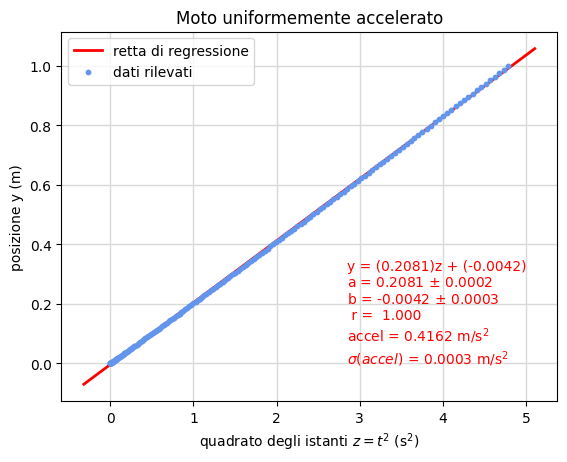
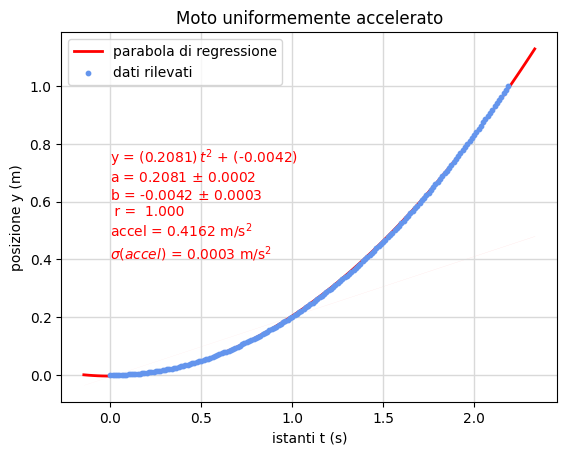
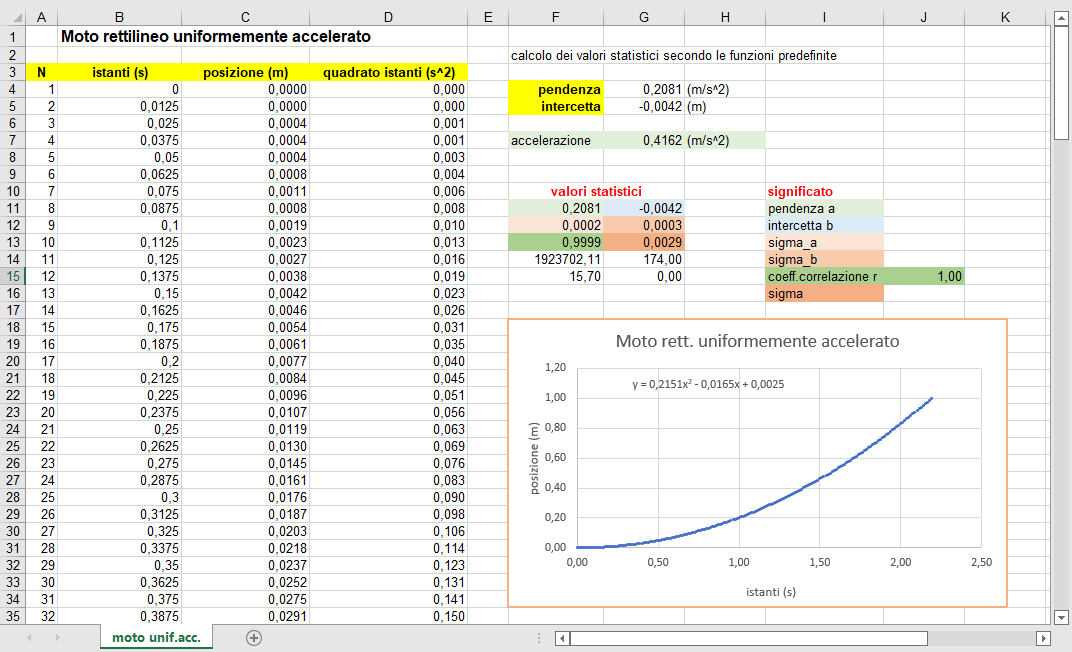
Moto uniformemente accelerato
Il moto uniformemente accelerato con partenza da fermo è descritto dalla legge cinematica quadratica \(s=(a/2)t^2+b\) facilmente linearizzabile non appena si disponga in ascissa il quadrato del tempo ponendo quindi \(z=t^2\). L'accelerazione si deduce dalla pendenza della retta di regressione moltiplicando quest'ultima per 2.
La figura 15 riporta, a sinistra, la retta di regressione con la variabile \(z\) in ascissa mentre nella parte destra viene visualizzata la parabola di regressione definita dai parametri ottenuti nella linearizzazione.
Nel foglio di calcolo motoAcc.xlsx riportiamo in figura la medesima parabola di regressione (non visibile in quanto sovrapposta dai dati) ma con aggiunta la sua equazione. Questa viene fornita dal foglio di calcolo dopo aver scelto per la linea di tendenza una funzione quadratica. La piccola differenza con i risultati precedenti è dovuta alla scelta (automatica) del foglio di produrre un polinomio dove sia presente anche il termine di primo grado.
Esperienza di Fletcher
Nell'esperienza di Fletcher ad un carrello di massa \(M\) posto su una rotaia a cuscino d'aria orizzontale vengono aggiunte \(n\) piccole masse \(m\) mentre una prima massa \(m\) è responsabile della trazione iniziale del carrello. Con l'accorgimento di mantenere la massa complessiva \(M_{tot}\) costante si sposta gradualmente ciascuna delle \(n\) masse sul carrello aggiungendole via via alla massa traente. In tal caso sussiste la proporzionalità tra l'accelerazione \(a\) del carrello e la massa traente \(m_t\) secondo la formula
\[ a=\Bigl({g\over M_{tot}}\Bigr)m_t. \] L'esperienza consiste quindi nel verificare questa proporzionalità stimando l'accelerazione con le modalità descritte nell'esperienza sul moto accelerato mentre per le masse sono sufficienti delle semplici pesate (la seconda prova nella tabella sottostante è quella descritta nell'esperienza precedente). Supposta nota l'accelerazione di gravità \(g\), diviene possibile un confronto tra l'accelerazione prevista secondo la formula precedente e l'accelerazione rilevata.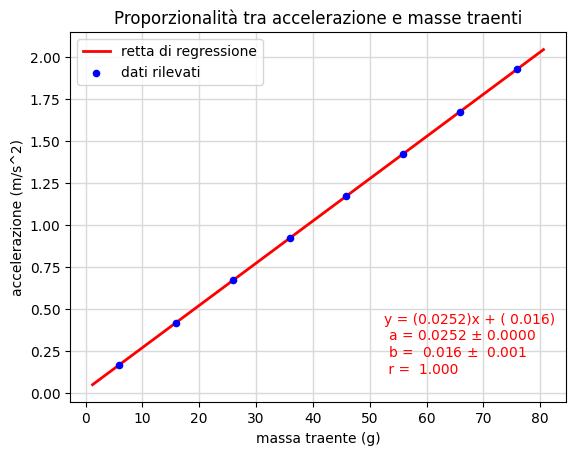
Nella tabella 2 sottostante prodotta, come la figura 17, dal notebook Fletcher.ipynb, riportiamo i dati di input assieme all'accelerazione prevista e al confronto con quella rilevata.
massa carrello (g) massa traente: m_t (g) acc.rilevata: a_r (m/s^2) acc.prevista: a_p (m/s^2) a_r-a_p (m/s^2)
-------------------- ------------------------ --------------------------- --------------------------- -----------------
367.9 5.9 0.1636 0.1548 0.01
357.9 15.9 0.4162 0.4173 -0.00
347.9 25.9 0.6701 0.6797 -0.01
337.9 35.9 0.9204 0.9422 -0.02
327.9 45.9 1.1690 1.2046 -0.04
317.9 55.9 1.4240 1.4670 -0.04
307.9 65.9 1.6710 1.7295 -0.06
297.9 75.9 1.9270 1.9919 -0.06
Legge di Boyle
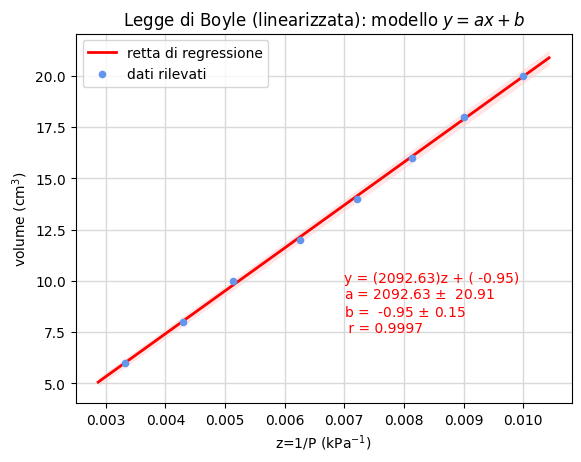
La legge di Boyle sui gas perfetti esprime la proporzionalità inversa tra volume \(V\) e pressione \(P\) durante una trasformazione isoterma di gas perfetto. Questa relazione è facilmente linearizzabile non appena si ponga in ascissa il reciproco della pressione. Posto quindi \(z=1/P\), la legge da verificare diviene \(V=a z+b\).
I valori ottenuti comprimendo gradualmente l'aria contenuta in una siringa graduata e connessa ad un sensore di pressione sono riportati nella figura 18. La scelta di porre in ascissa i reciproci dei valori della pressione si giustifica in quanto riteniamo che l'errore maggiore sia collegato al volume per il quale ipotizziamo un errore massimo pari a \(\Delta V=0.5\) cm\(^3\). Riteniamo invece trascurabile l'errore sulla pressione.
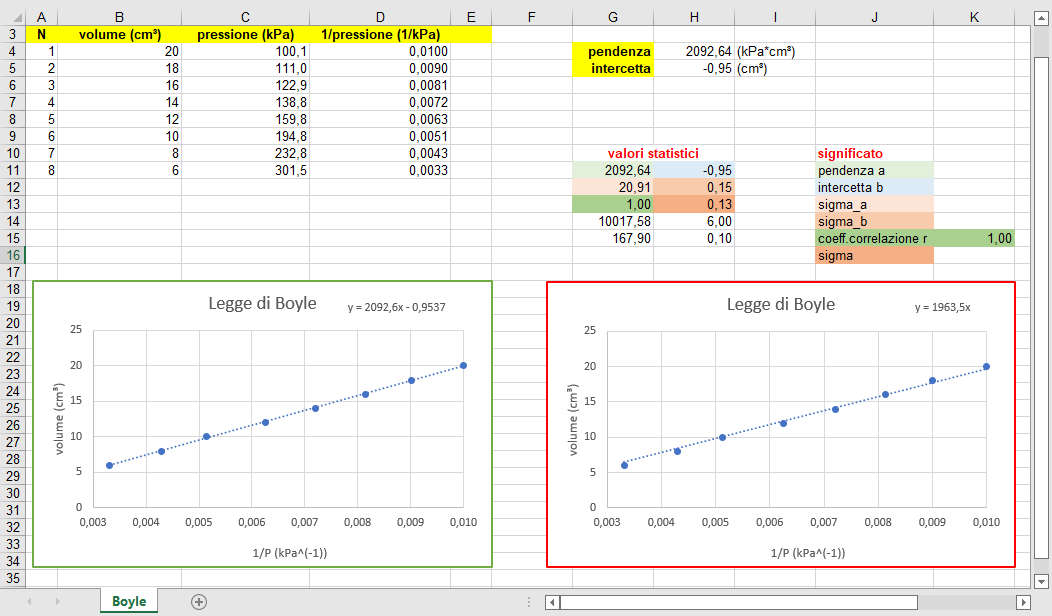
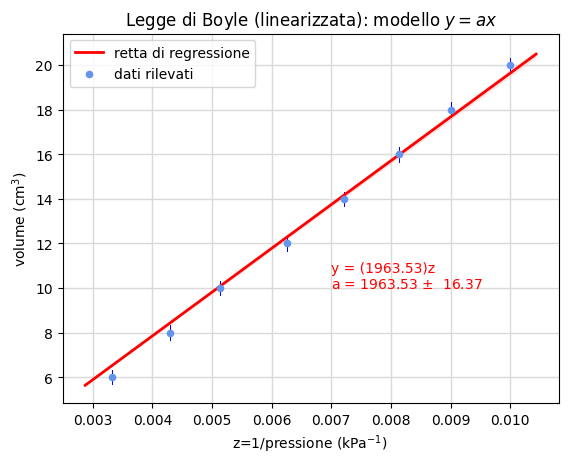
La figura 18 riporta il calcolo dei parametri del modello lineare. Nel secondo grafico, abbiamo invece selezionato il modello con intercetta nulla per cui la retta di regressione (o di tendenza) ha equazione \(y=ax\).
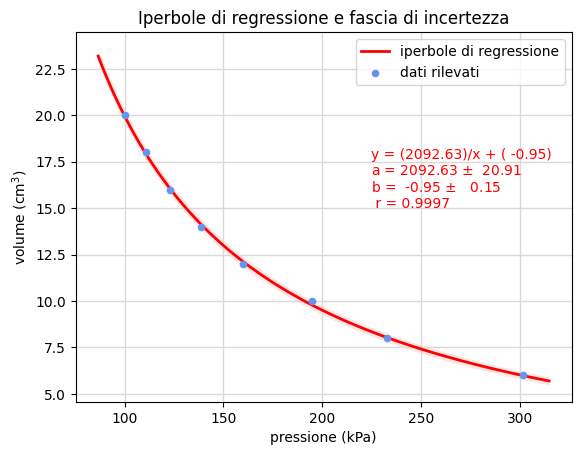
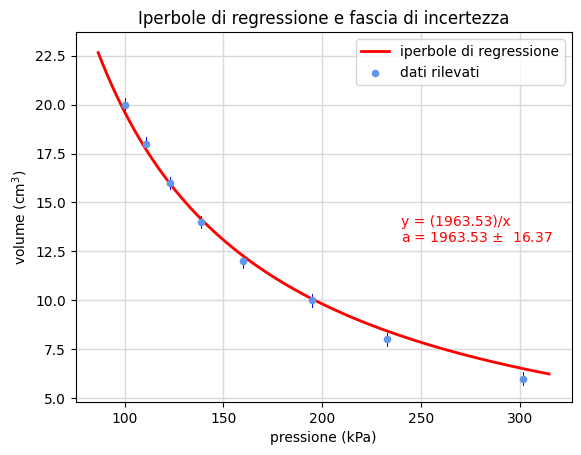
Nella figura 19 rappresentiamo i medesimi risultati ma ottenuti con il notebook Boyle.ipynb: tracciamo inoltre l'iperbole prodotta dalla linearizzazione di equazione \(V=\hat a/P+\hat b\).
La figura 20 riporta invece gli esiti dell'elaborazione ottenuti secondo il modello a intercetta nulla \(y=ax\).
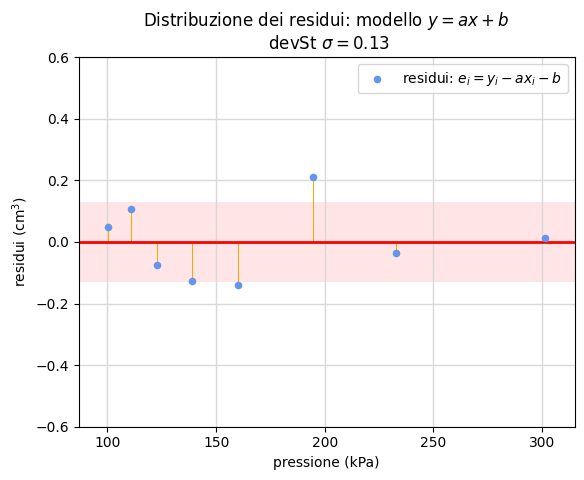
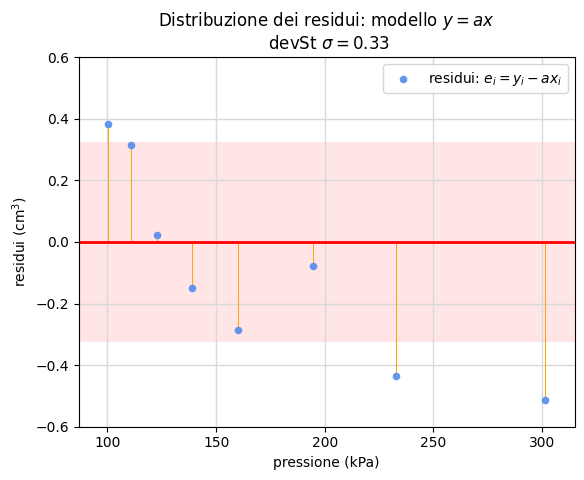
Infine nelle due immagini della figura 21 poniamo a confronto la distribuzione che si ottiene in ciascun modello: come anticipato nella discussione sulla prima legge di Ohm, il modello a intercetta nulla produce evidenti distorsioni che si riflettono in una maggiore deviazione standard dei residui.
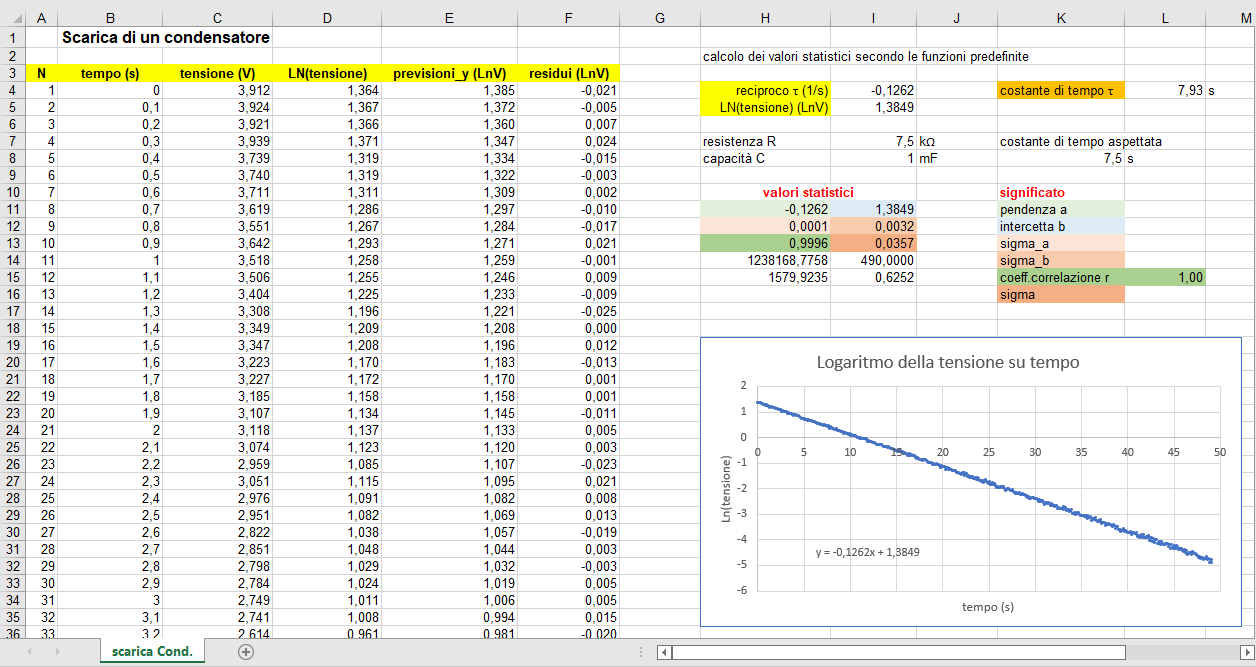
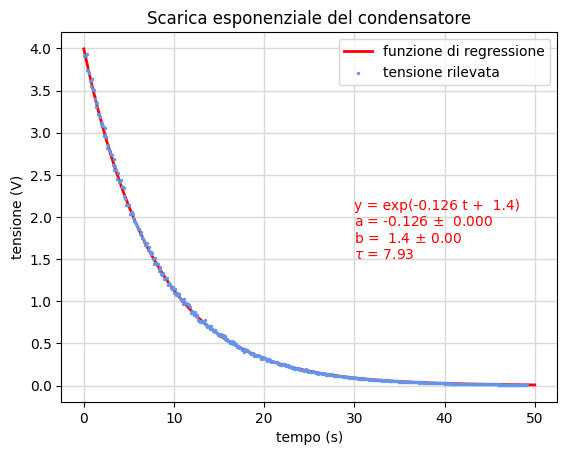
Scarica di un condensatore su resistore
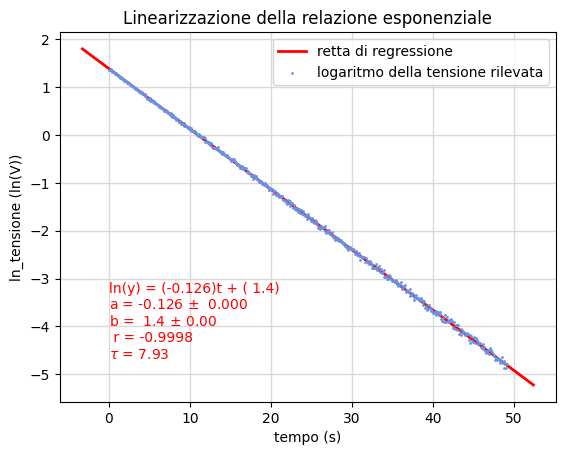
La legge con cui un condensatore di capacità \(C\), inizialmente carico, disperde le cariche sulle sue armature attraverso un resistore (resistenza \(R\)) segue un andamento esponenziale decrescente con la d.d.p. \(V\) tra le armature che dipende dal tempo \(t\) come
\begin{equation} V(t)=V_0\,e^{-t/\tau} \end{equation}essendo \(\tau=RC\) la costante di tempo del circuito e \(V_0\) la d.d.p. iniziale. Come discusso nella pagina di teoria, (42) e (43), questa espressione si può linearizzare in
\begin{equation} \log(V)=\log(V_0)- \frac{t}{\tau} \end{equation}per cui, posto \(z=\log(V)\), si riduce ad una relazione lineare \(z=b+at\) tra il logaritmo della tensione e il tempo. Ottenuti con la regressione i parametri ottimali \(\hat a\) e \(\hat b\) è immediato dedurre la costante di tempo \(\tau=-1/\hat a\) e la tensione iniziale \(V_0=\exp({\hat b})\) presenti nella legge esponenziale.
In figura 22 riportiamo parte del foglio di calcolo comprendente le circa 500 coppie di dati grezzi \((t_i,V_i)\) ottenute nell'arco di 50 secondi e la conseguente elaborazione.
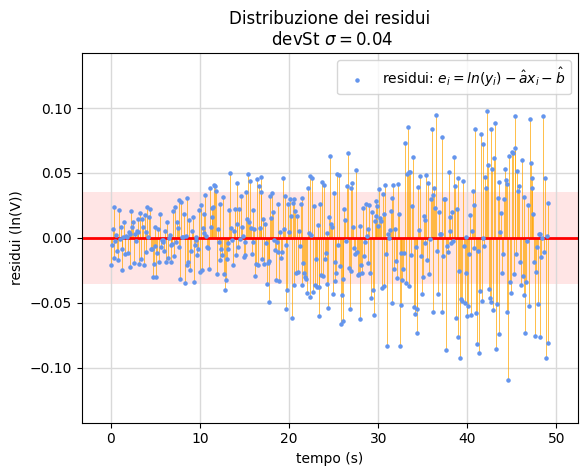
Le figure 23 e 24 riassumono gli esiti dell'elaborazione eseguita tramite il notebook Jupyter scarica.ipynb. Analogamente al grafico nella figura precedente, la figura 23 mostra le coppie linearizzate \((t_i,z_i)\) e la retta di regressione mentre alla destra riporta la distribuzione dei residui.
La figura 24 rappresenta invece tutte le coppie \((t_i,V_i)\) di dati grezzi e la funzione esponenziale che li interpola.
Un grazie all'amico tecnico Paolo Giacon per avermi fornito i dati aggiornati di questa esperienza.
Legge di Snell della rifrazione
Quale ultimo esempio di linearizzazione di una relazione e della conseguente applicazione del metodo di regressione lineare riportiamo le misure dell'angolo di incidenza e del corrispondente angolo di rifrazione ottenute, tramite un semplice disco di Hartl, facendo incidere uno stretto raggio di luce su un elemento di plexiglas a forma di mezzaluna.
i (deg) | 0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85
rf (deg) | 0 3 7 10 13 16 20 22 26 28 31 33 36 37 39 40 41 42
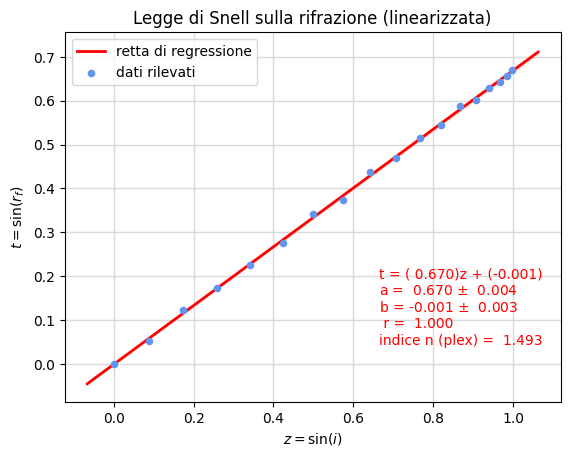
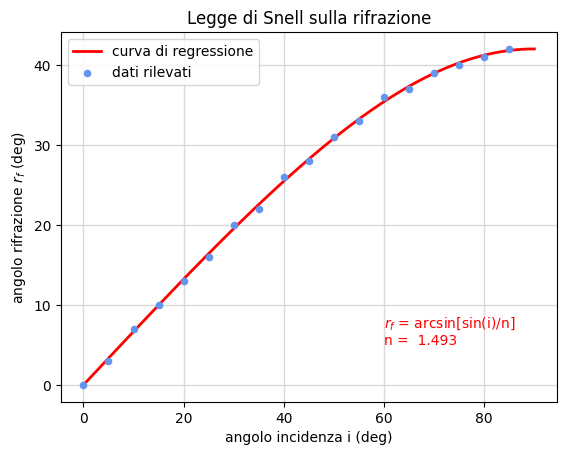
La legge di Snell nel caso il raggio passi dall'aria al plexiglas è \[n \sin(r_f)=\sin(i) \] per cui posto \(z=\sin(i)\) e \(t=\sin(r_f)\) la si riporta ad una relazione lineare \[\eqalign{t&=(1/n)z + b\cr &= a\, z+b\cr} \] dove, per i motivi già esposti in alcune delle precedenti esperienze, scegliamo il modello di regressione lineare in alternativa a quello con intercetta nulla. L'indice di rifrazione \(n\) è quindi collegato alla pendenza \(a\) dalla relazione \(n=1/a\).
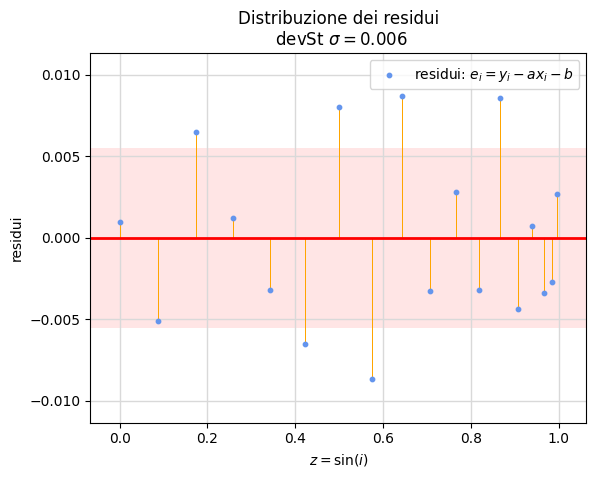
L'elaborazione con il notebook rifrazione.ipynb produce i risultati riportati nella figura 25. Questi, pur nella semplicità dell'apparato, permettono una stima soddisfacente per l'indice di rifrazione del plexiglas \(\hat n=1/\hat a=1.493\) e, data l'esiguità del parametro \(b\), confermano pienamente la legge.
Per un ulteriore confronto con la distribuzione dei dati grezzi iniziali (tabella 3), riportiamo l'insieme delle misure in un piano con entrambi gli assi espressi in gradi (deg) (fig. 26). Inoltre, riscritta la legge di Snell in forma di funzione dove l'angolo di rifrazione rappresenti la variabile dipendente da quello di incidenza \[ \sin(r_f)={\sin(i)\over \hat n}\qquad\Longrightarrow\qquad r_f=\arcsin\Bigl[{\sin(i)\over \hat n}\Bigr], \] il grafico di questa funzione nel medesimo piano conferma il buon accordo con la distribuzione delle misure (fig. 26).
Regressione circolare: diffrazione di Fraunhofer
La regressione circolare è senza dubbio meno frequente della regressione lineare ma può trovare una sua applicazione in un laboratorio didattico là dove sia necessario stimare il raggio di elementi che, per la particolare disposizione sperimentale, abbiano una forma circolare.
Il primo esempio che riportiamo riguarda la misura del raggio \(r_{1}\) del primo minimo di diffrazione prodotto dal passaggio di un fascio laser attraverso un'apertura circolare di diametro \(2a\). Se \(L\) è la distanza tra il foro e lo schermo e viene rispettata la condizione di Fraunhofer \(L≫ 2a\), la lunghezza d'onda della luce è, in questo caso, data dalla semplice espressione
\begin{equation} \lambda = {r_{1}(2a)\over 1.22\, L}. \end{equation}Ottenuta una foto della successione di massimi e minimi di diffrazione dove come sfondo si sia posto un foglio di carta millimetrata, la successiva rielaborazione con un qualsiasi software grafico permette la lettura delle coordinate di un adeguato numero di pixel associati al primo minimo. Salvate queste coordinate in un file CSV, l'elaborazione di questo con il notebook diffrazione.ipynb fornisce il valore in pixel del raggio. Infine, per la presenza del foglio millimetrato una semplice proporzione riporta il valore di \(r_1\) in metri che, inserito nella formula precedente con i restanti parametri, permette di ottenere la lunghezza d'onda \(\lambda\).
In figura 27 riportiamo la foto del massimo centrale di diffrazione assieme al primo minimo e nella parte destra sovrapponiamo, a solo scopo esemplificativo, la circonferenza di regressione con i punti rilevati.
Nota. Con un adeguato, ma elementare, software grafico è evidentemente possibile tracciare, per tentativi, una circonferenza e adattarla visivamente a quella del minimo per poi leggerne direttamente il raggio in pixel.
Traiettoria circolare di elettroni in campo magnetico
La misura del rapporto tra carica \(e\) e massa \(m\) dell'elettrone o carica specifica si ottiene in un laboratorio didattico ponendo un fascio di elettroni (fascio filiforme), inizialmente accelerati da una differenza di potenziale \(\Delta V\), in un campo magnetico uniforme \(B\) perpendicolare alla loro velocità. L'urto degli elettroni all'interno di un'ampolla dove vi sia un gas rarefatto, eccita gli atomi del gas e questi, decadendo allo stato fondamentale, emettono dei fotoni nella banda del visibile. In tal modo si rende visibile il percorso del fascio di elettroni all'interno del tubo e diviene possibile stimare il raggio delle loro traiettorie (fig. 28).

Con l'accorgimento di associare alla foto del fascio di elettroni un elemento che fornisca il rapporto metri/pixel (il righello graduato nella figura 28 posto nello stesso piano del fascio), si possono individuare su questa quei punti attraversati dal fascio circolare. Memorizzate in un file CSV le rispettive coordinate, il notebook motoElettroni.ipynb, nel quale applichiamo in alternativa a quello geometrico il modello algebrico, permette di ottenere il raggio in pixel ed, eseguita l'opportuna proporzione, la misura \(r\) in metri della traiettoria. Questo risultato va infine inserito nella formula
\[ {e\over m}={2\,\Delta V\over (B\, r)^2} \] essendo \(\Delta V\), come detto, la differenza di potenziale responsabile dell'accelerazione iniziale degli elettroni e \(B\) il campo magnetico uniforme generato da due bobine di Helmholtz. Il valore di \(B\), in mancanza di una sonda che ne dia direttamente il valore, si ottiene dalla lettura, dopo adeguata taratura, della corrente che percorre le due bobine.La figura 29 riporta la medesima foto del fascio di elettroni con nella parte destra sovrapposta la circonferenza ottimale e i punti selezionati per ottenerla.
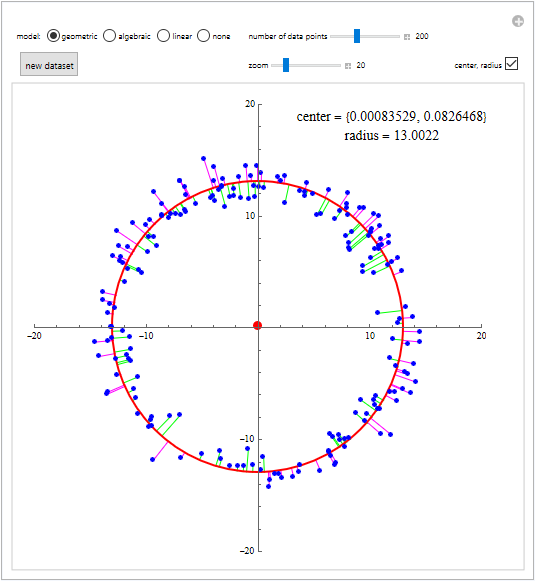
Simulazione della regressione circolare
L'immagine seguente richiama la "demonstration" pubblicata all'indirizzo https://demonstrations.wolfram.com/CircularRegression e permette, se avviata con Mathematica o con il gratuito Wolfram Player, di sperimentare in modo interattivo con la regressione circolare.
Scelto il numero di punti da cui partire, la circonferenza ottimale viene ottenuta applicando uno dei modelli esposti nella parte teorica e cioè
- il modello geometrico,
- il modello algebrico e
- il modello lineare che, come accennato nella pagina di teoria, discende da quello algebrico non appena si facciano nella funzione obiettivo (60) le sostituzioni (61).
Selezionando alternativamente il modello e mantenendo costante il numero dei dati si potranno cogliere le lievi differenze nei valori, restituiti da ciascun modello, per le coordinate del centro e il raggio.

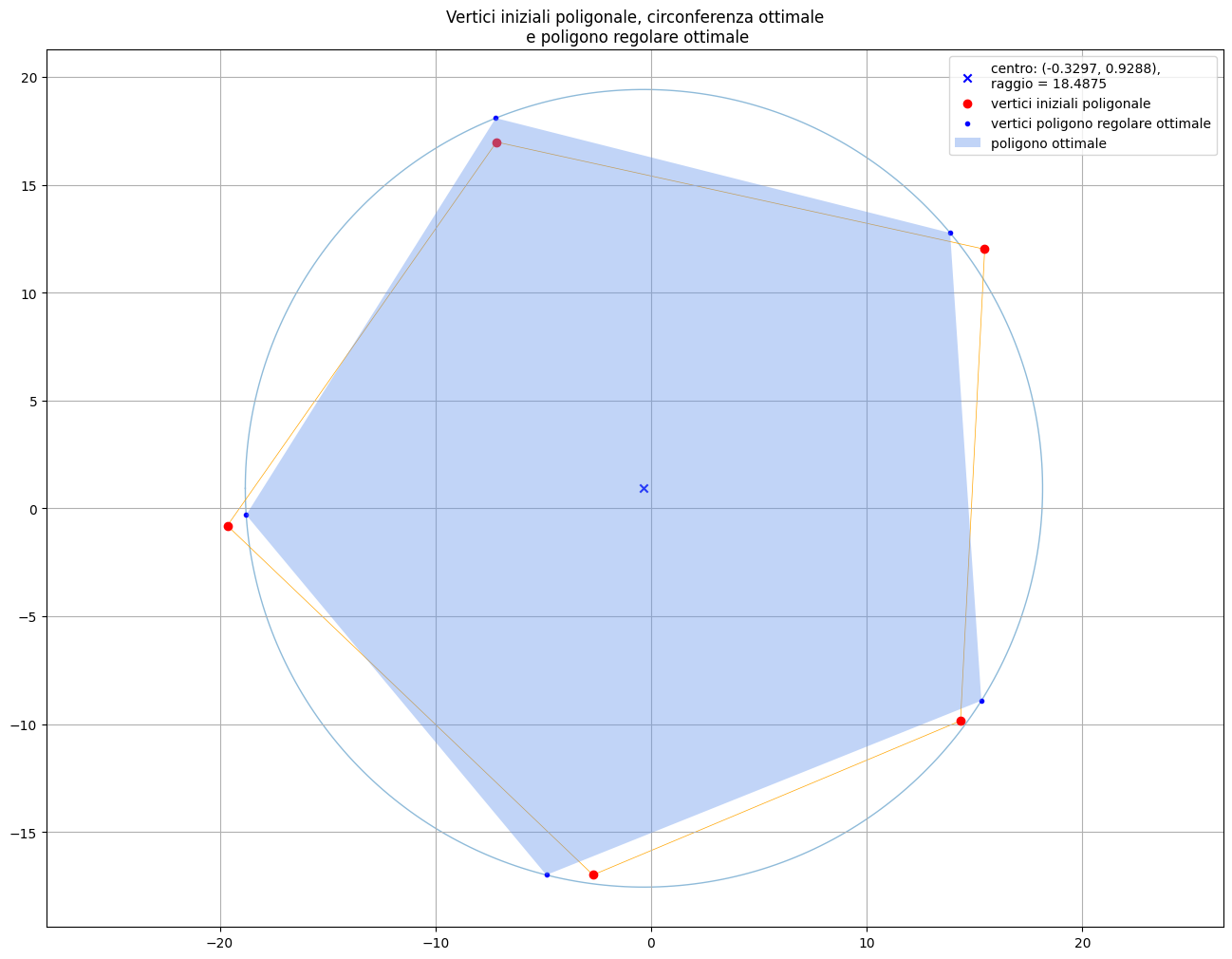
Dalla poligonale al poligono regolare
Il link seguente rimanda ad un repository GitHub
dove proponiamo una applicazione di carattere geometrico della regressione circolare. A partire da una poligonale di \(n\) vertici, viene dapprima individuata la circonferenza che interpola in modo ottimale i vertici e quindi si determina il poligono regolare che meglio si avvicina alla poligonale.
Il repo contiene principalmente due file:
- il programma Python poligonoRegolare.py e
- il notebook Jupyter poligonoRegolare.ipynb:
quest'ultimo si potrà avviare in forme interattive anche online tramite Binder.
Il link sottostante fornisce invece un'anteprima locale del notebook.