Esperienze di Fisica
In questa pagina presentiamo lo studio della legge della rifrazione per mezzo del disco di Hartl e parallelamente all'osservazione sperimentale associamo una simulazione (Demonstration di Mathematica) per facilitare la comprensione della geometria dell'apparato e l'interpretazione dei risultati.
Il disco di Hartl e la legge di Snell della rifrazione
- Misure aria → plexiglas
- Misure plexiglas → aria
- Osservazioni...fuori asse
- Risorse didattiche e persone
Il disco di Hartl è costituito da un disco metallico suddiviso in quattro quadranti graduati in gradi in modo da formare un goniometro e montato su di un supporto girevole attorno al suo asse centrale che, a seconda dei modelli, può essere disposto orizzontale (figura) o verticale. Su di esso si possono montare vari elementi trasparenti generalmente di polimetilmetacrilato (plexiglas) quali prismi triangolari o trapezoidali, lenti cilindriche e/o semicircolari, specchi, così da studiare le deviazioni subite da uno stretto fascio luminoso opportunamente collimato e proveniente da un proiettore (figura) o, in alternativa, da un piccolo insieme di raggi paralleli.
Nella semplice esperienza che qui si propone l'elemento di plexiglas ha la forma di una mezzaluna di color arancio e l'intendimento principale è di verificare la legge della rifrazione o legge di Snell. In quanto segue riportiamo pertanto le varie misure accompagnando le più significative con le foto del disco e con l'immagine della corrispondente simulazione.
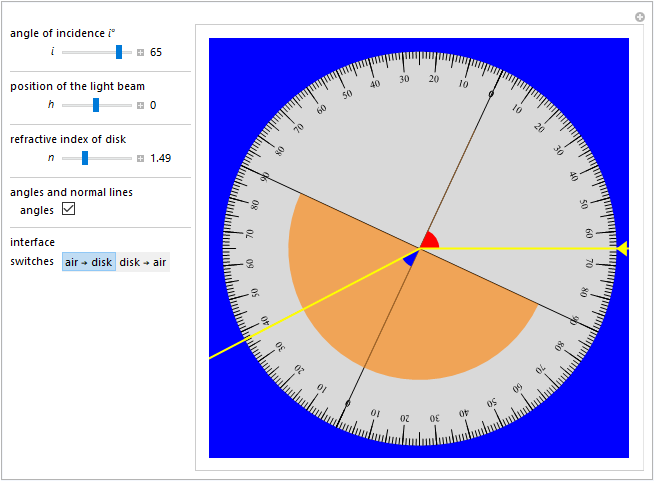
Poiché non è sempre immediato comprendere l'importanza della centratura del raggio incidente, proponiamo anche la simulazione dell'apparato tramite la "Demonstration" di Mathematica. Inoltre riportiamo anche alcuni esempi con la direzione del raggio incidente fuori asse. Almeno, nei casi più semplici, questi possono fornire anche un'occasione didattica per riprodurre, tramite GeoGebra, il percorso seguito dal raggio luminoso.

Misure aria → plexiglas
Predisposta la mezzaluna come in figura cosicché il raggio incidente (da destra nella foto) incida normalmente sulla superficie aria/plexiglas e il raggio rifratto emerga dalla mezzaluna di plexiglas non deviato (e quindi incide altrettanto normalmente sul lato curvo della mezzaluna),
 |
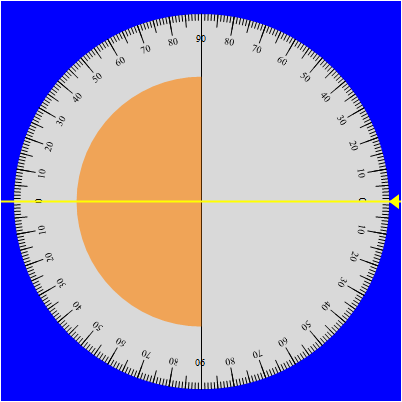 |
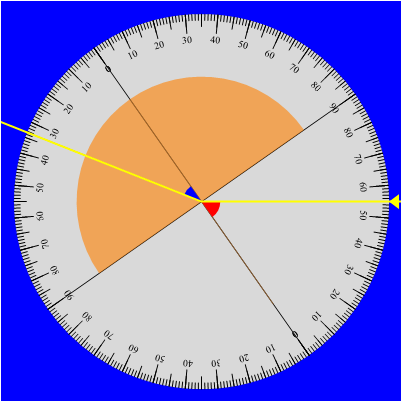
le misure dell'angolo di incidenza si ottengono immediatamente dato che la normale al punto di incidenza sulla parte piana coincide con la traccia normale riportata sul disco corrispondente allo zero e dalla stessa parte del raggio incidente. Se il sistema è adeguatamente centrato il raggio rifratto entro la mezzaluna di plexiglas incide quindi normalmente sull'interfaccia curva plexiglas/aria per cui, come nella situazione iniziale, non subisce alcuna deviazione. L'angolo di rifrazione è perciò formato dalla normale al punto di incidenza (indicata ancora con lo zero ma dalla parte del raggio emergente) con la direzione del raggio emergente stesso. Agendo in tal modo, le coppie angolo di incidenza e angolo di rifrazione (rispettivamente indicati nelle immagini associate alle foto in rosso e in blu) si ottengono ruotando via via il disco e seguono immediate.
La simulazione proposta alla fine permette di chiarire la situazione geometrica appena descritta mostrando come sia invece problematico rilevare l'angolo di rifrazione internamente al plexiglas se tali condizioni geometriche non vengono rispettate.
 |
 |
 |
 |
 |
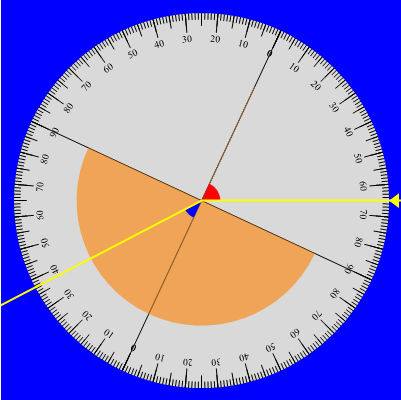 |
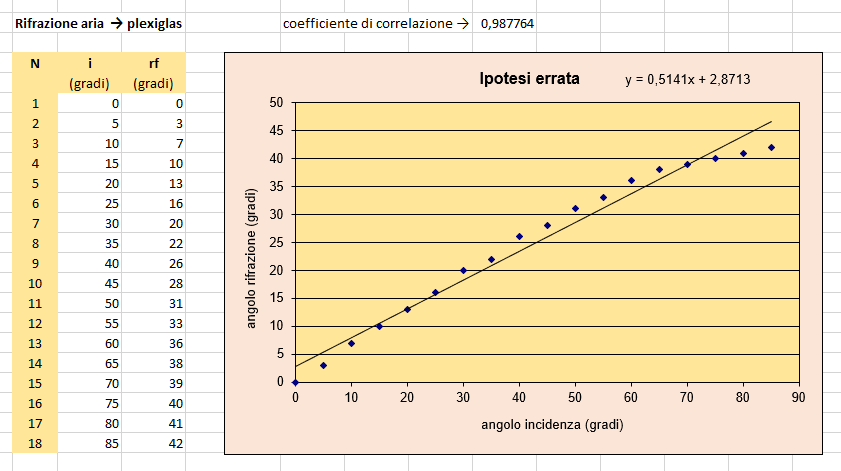
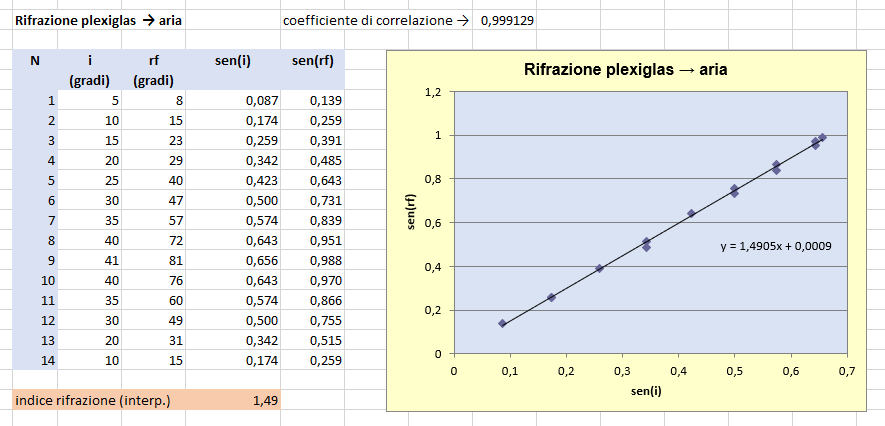
Un primo insieme di misure dell'angolo di incidenza i e dell'angolo di rifrazione, rf, è riportato sotto con accanto la rappresentazione grafica delle coppie di misure. L'ipotesi più immediata ossia che sussista una relazione lineare tra l'angolo di incidenza e quello di rifrazione appare per angoli piccoli anche adeguata ma viene significativamente smentita all'aumentare degli stessi mostrando questi un andamento curvilineo piuttosto che una dispersione casuale attorno alla retta di regressione. Il coefficiente di correlazione assume per tali coppie di misure il valore 0,9878.
In corrispondenza delle medesime coppie di dati calcoliamo invece i valori della funzione seno e rappresentiamo quindi nella figura successiva le coppie (sen(i), sen(rf)). In tal modo appare con evidenza una relazione lineare e, in particolare, di proporzionalità tra il seno dell'angolo di incidenza e il seno dell'angolo di rifrazione, fatto confermato pure dal valore del coefficiente di correlazione molto prossimo ad 1. Vale pertanto la legge della rifrazione sen(i)/sen(rf) = n12 con n12 costante di proporzionalità detta indice di rifrazione del mezzo 2 rispetto al mezzo 1.
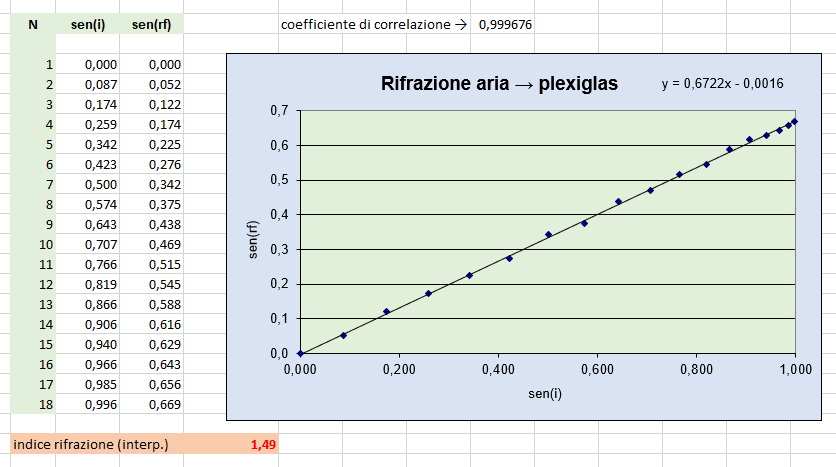
Poiché si è scelto di rappresentare il sen(rf) in ordinata, l'indice di rifrazione del plexiglas rispetto all'aria (vuoto) si ottiene considerando il reciproco del coefficiente angolare della retta di regressione e quindi la serie riportata fornisce l'apprezzabile risultato n12 = 1.49.
Misure plexiglas → aria
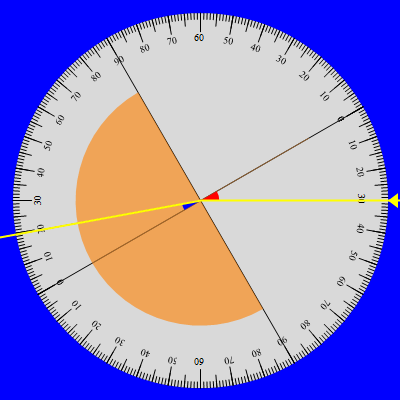
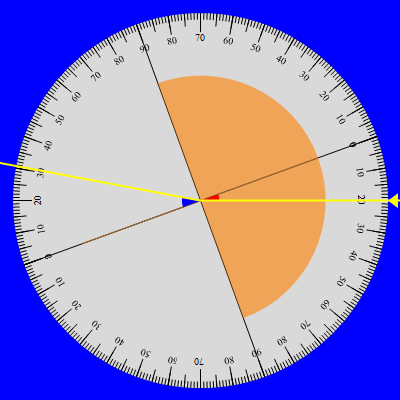
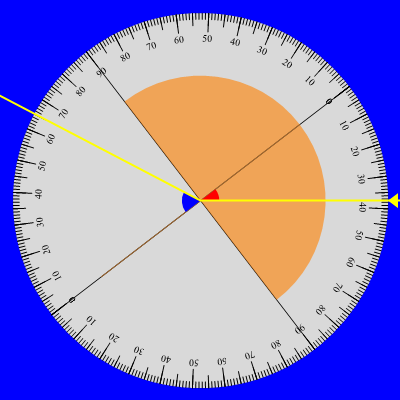
Una rotazione di 180 gradi del disco permette di studiare la rifrazione nell'ordine inverso ossia plexiglas → aria. In tal caso l'incidenza normale avviene nel passaggio aria/plexiglas e il raggio incidente sulla parte piana della mezzaluna possiede quindi la medesima direzione iniziale. L'angolo di incidenza è formato dalla direzione iniziale con la linea normale al punto di incidenza (e centro del disco), indicata sul disco ancora dallo zero e dalla parte del raggio incidente. Altrettanto, l'angolo di rifrazione è ora definito dalla direzione del raggio rifratto in aria con la linea normale al punto di incidenza e dalla parte del raggio rifratto.
 |
 |
 |
 |
 |
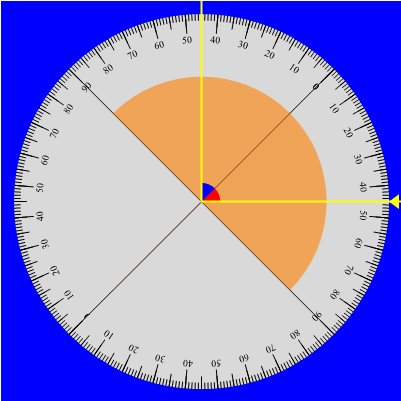 |
Di seguito riportiamo la nuova serie di misure ottenuta aumentando gradualmente l'angolo di incidenza fino a valori prossimi all'angolo limite, situazione questa che impone una stima sempre più approssimativa del raggio rifratto. Verificata l'esistenza di un angolo limite oltre il quale il raggio incidente è totalmente riflesso (terza coppia delle immagini sopra) le misure dell'angolo di incidenza riprendono alcuni valori già considerati mentre in corrispondenza l'angolo di rifrazione appare leggermente diverso fornendo in tal modo una stima dell'incertezza complessiva delle misure. Ciò nonostante e come dimostra il grafico associato, la distribuzione delle coppie (sen(i), sen(rf)) è ben descritta dalla retta di regressione che pertanto conferma la proporzionalità di sen(rf) con sen(i).
Riprese dalle due serie di misure precedenti le coppie di angoli di figura e le confrontiamo,
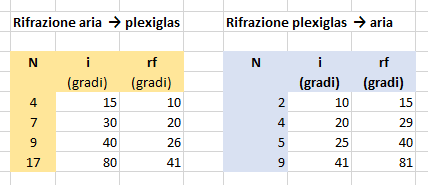
appare che a meno di un grado, valore che possiamo identificare con l'errore dell'apparato, le misure degli angoli di incidenza e rifrazione appaiono scambiate. Ciò suggerisce come il percorso di un raggio luminoso possa essere semplicemente invertito dato che la coppia di angoli coinvolti nella legge non cambia pur scambiando il significato dei due angoli coinvolti. Più formalmente, poiché la retta di regressione descrive in tal caso la relazione sen(rf) = n12 sen(i) il suo coefficiente angolare si identifica con l'indice di rifrazione del plexiglas rispetto all'aria ed è in completo accordo con quanto ottenuto nella prima serie di misure. Ovviamente n21 = 1/n12 = 0.67 rappresenta il suo reciproco cioè l'indice di rifrazione relativo dell'aria rispetto al plexiglas.
In definitiva, se l'angolo di incidenza appartiene al mezzo 1 e quello di rifrazione al mezzo 2, abbiamo verificato la legge di Snell della rifrazione sen(i)/sen(rf) = n12 con n12 indice di rifrazione del mezzo 2 relativamente al mezzo 1.
Osservazioni...fuori asse
L'immagine sottostante rappresenta una "Demonstration" creata con Mathematica tramite la quale si può simulare l'esperienza sulla legge di Snell con il disco di Hartl e quindi studiare il fenomeno della rifrazione luminosa.
Se la si utilizza con il fascio centrato si riproduce quanto descritto precedentemente mentre traslandolo si può innanzitutto comprendere l'importanza della centratura per la corretta misura degli angoli di incidenza e rifrazione. Nell'ipotesi che, internamente al corpo rifrangente, il raggio non subisca alcun assorbimento e quindi alcuna estinzione e agendo sui tre pulsanti così da modificare
- l'angolo di incidenza (o anche inclinazione della mezzaluna),
- la posizione del fascio e
- l'indice di rifrazione del mezzo,
si possono visualizzare i diversi percorsi seguiti dalla luce fino alla sua emergenza.
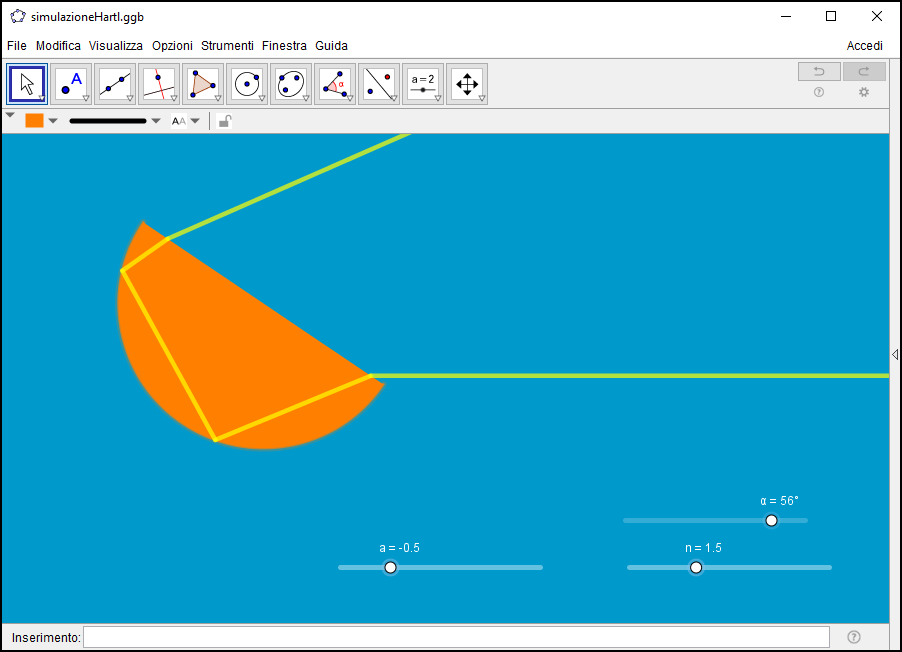
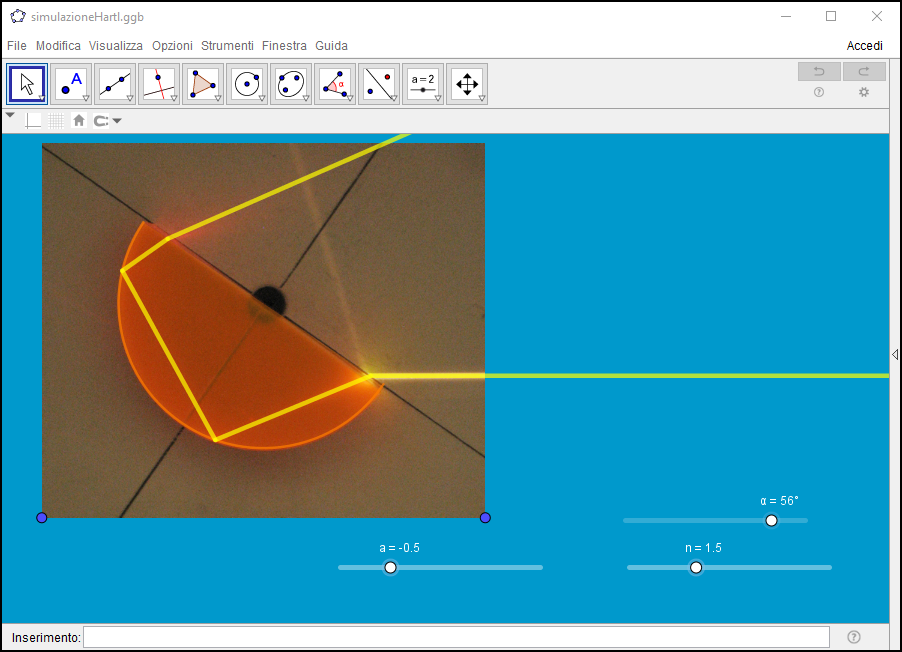
Nella foto che segue il fascio è quindi disposto fuori asse per cui il percorso della luce appare più complicato anche a seguito delle riflessioni totali subite. Ricostruiamo tale situazione esemplificativa con due sue riproduzioni: la prima associandola alla "Demonstration" di Mathematica, la seconda con una costruzione ad hoc eseguita con GeoGebra.
 |
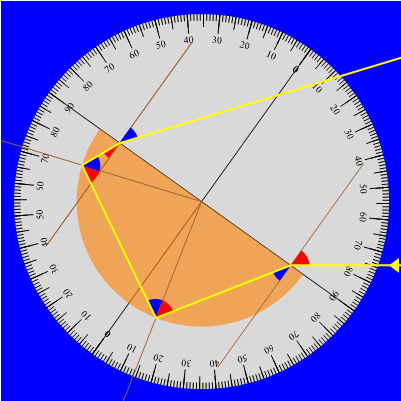 |
Costruzione di GeoGebra nella quale si possono variare (entro limiti abbastanza ristretti per mantenerne la correttezza) i parametri geometrici e fisici.
La medesima costruzione precedente con sovrapposta la foto ottenuta in laboratorio.
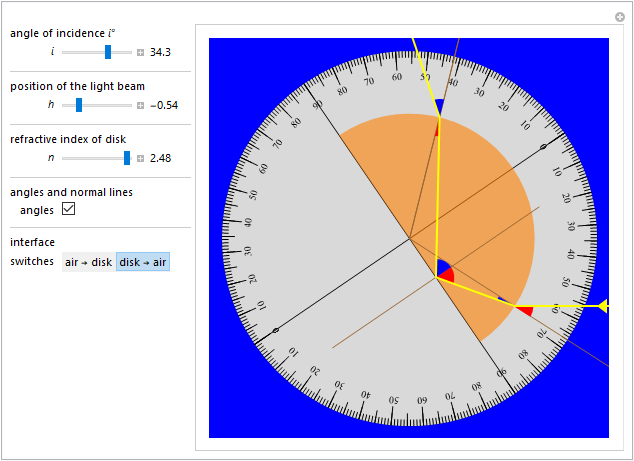
Concludiamo proponendo una piccola rassegna di percorsi luminosi alcuni dei quali mostrano configurazioni anche abbastanza curiose.
 |
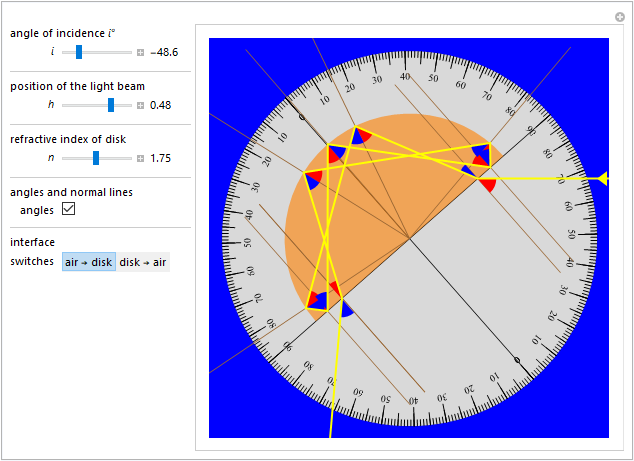 |
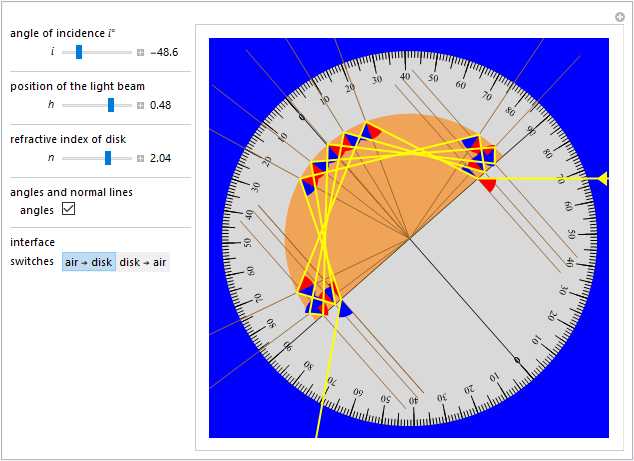 |
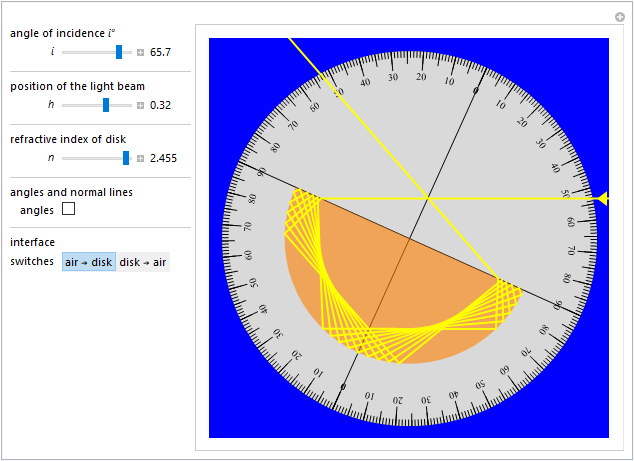 |
Risorse didattiche e persone
I file della simulazione sono prelevabili dal sito demonstrations.wolfram.com sia nel formato notebook NB di Mathematica (Author Code) e sia nel formato CDF. Quest'ultimo formato permette di utilizzare interattivamente la simulazione se nel proprio sistema è installato il gratuito CDF Player.
Gli altri materiali didattici qui utilizzati costituiti da un foglio di calcolo e da un file di GeoGebra sono prelevabili tramite il link sottostante.
Infine un particolare ringraziamento al tecnico di laboratorio, sig. Paolo Giacon, non solo per la cura nella predisposizione dell'esperienza e nelle riprese fotografiche per le quali si è dimostrato necessario un particolare allestimento ma, e soprattutto, per la sua costante disponibilità.