La nefroide
- Note storiche
- Le curve epicicloidi
- La nefroide come epicicloide
- La nefroide come caustica di riflessione
- Un secondo inviluppo di rette
- Un inviluppo di circonferenze
- La nefroide come luogo
Note storiche
La nefroide è una curva del piano che si forma per riflessione da uno specchio sferico quando su di esso incide un fascio di raggi paralleli: è quindi una caustica di riflessione. Questa osservazione, riportata per la prima volta nel 1678 da Christiaan Huygens (1629-1695) fu poi pubblicata nel Trattato sulla luce nel 1690. Il nome deriva dal Greco nephros che significa "rene" come, in effetti, ricorda la sua forma. Questo termine fu introdotto da Richard Proctor (1837-1888) nel suo trattato sulle cicloidi del 1878.
Le curve epicicloidi
La costruzione della curva nefroide che intendiamo qui proporre non fa uso dei classici strumenti della geometria euclidea, riga e compasso, per determinare un suo punto (si veda per questo approccio l'ultima sezione) ma individueremo comunque un suo punto con osservazioni di carattere fisico. Lo studio di un caso generale con semplici relazioni vettoriali ci permetterà di dedurre poi alcuni interessanti casi particolari. Innanzitutto diamo una definizione:
si dice che una curva è una epicicloide se viene generata da un punto che appartiene ad una circonferenza che rotola senza strisciare sulla superficie esterna di una seconda circonferenza fissa
Figura 4.1. nefroide01.ggb.
- Definita quindi una circonferenza c di raggio \(AB=R\) centrata nell'origine A di un sistema cartesiano (fig. 4.1),
- sia \(\alpha\) uno slider rappresentativo di un angolo che permette di determinare il punto D di c tramite lo strumento Angolo di data misura
 in modo tale che \(\angle(BAD)=\alpha\) (GeoGebra aggiunge l'etichetta \(\beta\)).
in modo tale che \(\angle(BAD)=\alpha\) (GeoGebra aggiunge l'etichetta \(\beta\)). - In tal modo è determinata anche la semiretta AD di origine A.
- Introdotto un secondo slider numerico b per rappresentare il raggio della seconda circonferenza e variabile tra 0 e raggio[c] (nel caso in esame è \([0,1]\) con \(b=0.5\)),
- con centro in D tracciamo una circonferenza di raggio pari a b
 e
e - sia C il punto di intersezione di questa con la semiretta \(AD\) esterno alla circonferenza c. Nascondiamo quindi questa circonferenza e
- tracciamo invece una terza circonferenza, e, questa volta di centro C e raggio \(b=CD\) e sia
- E il punto in cui questa interseca ulteriormente la semiretta AD.
Dobbiamo ora determinare un punto P su quest'ultima circonferenza in modo da simulare la rotazione che, in figura 4.1, appare essere descritta dall'angolo \(\angle(BAD)=\beta\). In corrispondenza di tale angolo il punto B, inizialmente sull'asse x, verrà a trovarsi in D e quindi avrà percorso (in un dato intervallo di tempo) l'arco \(BD\) (in blu in fig. 4.1). Con termini mutuati dalla fisica, poiché nel punto di contatto le velocità periferiche dei punti delle circonferenze c ed e sono uguali (altrimenti vi sarebbe scivolamento e non rotazione), un punto qualsiasi sulla circonferenza e, per esempio E (preferiamo tale punto anziché D per coerenza con altre costruzioni di questo sito), dovrà in corrispondenza percorrere, nel medesimo intervallo, un arco di lunghezza pari all'arco \(BD\) trovandosi infine in P (fig. 4.1). La condizione che assicura il rotolamento è quindi, nel medesimo intervallo di tempo, l'uguaglianza degli archi percorsi. Le rispettive lunghezze sono date dal prodotto dei raggi per gli angoli al centro sottesi da questi archi ed espressi in radianti. In formule questa condizione si esplicita in \[R\cdot\angle(BAD)=r\cdot\angle(ECP)\] da cui possiamo ricavare l'angolo \(\gamma=\angle(ECP)\) che risulta \begin{equation}\angle(ECP) = {R\over r}\angle(BAD)\qquad\hbox{e più sinteticamente}\qquad \gamma={R\over r}\beta.\label{eq:1}\end{equation} Nella costruzione di figura 4.1, P si ottiene con una rotazione del punto E attorno al centro C pari a \((1/b)\alpha\).
Non ci rimane che ottenere le coordinate del punto P. Tracciati quindi i vettori \(\vec{u}=\vec{AC}\) e \(\vec{v}=\vec{CP}\) risulta \begin{equation}\vec{AP}=\vec{AC}+\vec{CP}.\label{eq:2}\end{equation} D'altra parte, il modulo di \(\vec{AC}\) è pari a \(\bigl|\vec{AC}\bigr|=R+r\) mentre le sue componenti sono definite dall'angolo \(\beta\) e risultano \begin{equation}\vec{AC}=\bigl((R+r)\cos\beta, (R+r)\sin\beta\bigr).\label{eq:3}\end{equation} Per determinare le componenti di \(\vec{CP}\), il cui modulo è \(\bigl|\vec{CP}\bigr|=r\), è sufficiente tracciare le parallele agli assi coordinati per il punto C. L'angolo che questo vettore fa con l'asse x è allora dato dalla somma di \(\beta+\gamma\) che per \eqref{eq:1} diviene \begin{equation}\beta+\gamma=\beta+{R\over r}\beta=\biggl(\!1+{R\over r}\biggr)\beta\label{eq:4}\end{equation} e quindi \(\vec{CP}\) ha per componenti \begin{equation}\vec{CP}=\bigl(r\cos(\beta+\gamma), r\sin(\beta+\gamma)\bigr)=\biggl(\!r\cos\biggl(\!1+{R\over r}\biggr)\beta, r\sin\biggl(\!1+{R\over r}\biggr)\beta\!\biggr).\label{eq:5}\end{equation} Le componenti quindi di \(\vec{AP}\) sono per le \eqref{eq:2}, \eqref{eq:3} e \eqref{eq:5} \begin{equation}\vec{AP}=\bigl((R+r)\cos\beta, (R+r)\sin\beta\bigr)+\bigl(r\cos(\beta+\gamma), r\sin(\beta+\gamma)\bigr)\end{equation} ossia per la \eqref{eq:4}\begin{equation}\vec{AP}=\biggl((R+r)\cos\beta+r\cos\biggl(\!1+{R\over r}\biggr)\beta,\quad (R+r)\sin\beta+r\sin\biggl(\!1+{R\over r}\biggr)\beta\biggr)\end{equation}
In definitiva le equazioni parametriche di un punto P che appartiene ad una epicicloide sono \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x=(R+r)\cos\beta+r\cos\biggl(\!1+{R\over r}\biggr)\beta\cr\\[2pt] y= (R+r)\sin\beta+r\sin\biggl(\!1+{R\over r}\biggr)\beta\cr}}\label{eq:8}\end{equation}
La nefroide come epicicloide
Sulla base del risultato precedente può discendere una intera classe di curve, evidentemente, dipendente dal rapporto dei raggi delle due circonferenze (è questa la ragione dello slider b in fig. 4.1). Nella fig. 4.1 abbiamo scelto un rapporto pari a \(R/r=2\) e questo rapporto dà origine alla curva nefroide che perciò rientra tra le curve epicicloidi (fig. 4.2).
Figura 4.2. nefroide02.ggb.
Le equazioni \eqref{eq:8} si riducono in questo caso alle \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x={R\over 2}\bigl(3\cos\beta+\cos 3\beta\bigr)\cr\cr y={R\over 2}\bigl(3\sin\beta+\sin 3\beta\bigr).\cr}}\label{eq:eqnefroide}\end{equation}
Se invece il rapporto tra i raggi è pari all'unità, la curva che ne discende è pure una curva importante, la cardioide (fig. 4.3). Questa, diversamente dalla nefroide che ne presenta due, ha un'unica cuspide e le sue equazioni parametriche sono \begin{equation}\cases{x=R\bigl(2\cos\beta+\cos2\beta\bigr)\cr y= R\bigl(2\sin\beta+\sin2\beta\bigr).\cr}\end{equation}
Figura 4.3. card03.ggb.
La nefroide come caustica di riflessione
In questa sezione presentiamo la deduzione della nefroide come inviluppo delle sue rette tangenti. Ancora con terminologia fisica, queste rette si possono interpretare come raggi riflessi da uno specchio sferico su cui incide un fascio di raggi paralleli provenienti da un punto infinitamente distante. In tal caso si dice che la curva nefroide è la caustica di riflessione da parte di uno specchio sferico su cui incide il fascio di raggi paralleli.
Figura 4.4. nefroide04.ggb.
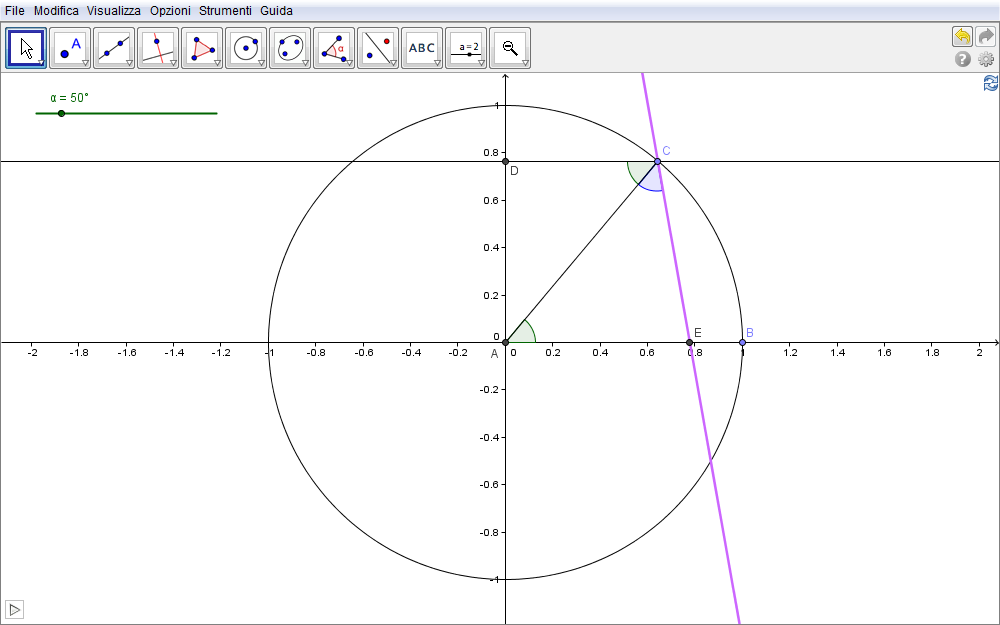
- Tracciata la circonferenza di raggio \(AB=R\) (unitario in fig. 4.4) con centro nell'origine A del sistema,
- definiamo lo slider angolare \(\alpha\)
- rappresentativo dell'angolo al centro \(\beta=\angle(BAC)\).
- Se ora consideriamo una retta parallela b all'asse x passante per C
- questa forma un angolo pari a \(\beta\) con il raggio AC (\(\angle(BAC)=\angle(ACD)\) essendo D il punto di b sull'asse y).
- Con lo strumento simmetria assiale
 , tracciamo infine la retta simmetrica a b rispetto al raggio AC e sia E il suo punto di intersezione con l'asse x.
, tracciamo infine la retta simmetrica a b rispetto al raggio AC e sia E il suo punto di intersezione con l'asse x.
Evidentemente \(\angle(ACE)=\angle(ACD)\) per cui \(\angle(ECD)=2\angle(BAC)=2\beta\) e, ricordando che il coefficiente angolare di una retta \(m_{CE}\) è pari alla tangente goniometrica dell'angolo orientato che questa fa con l'asse x, dev'essere \begin{equation}m_{CE}=\tan(\angle BEC)=\tan(\angle ECD)=\tan 2\beta\label{eq:9}\end{equation} per cui l'equazione della retta CE è \begin{equation}CE: y-y_C=m_{CE}(x-x_C)\end{equation} o anche \begin{equation}CE:y-R\sin\beta=\tan 2\beta\,(x-R\cos \beta).\label{eq:10}\end{equation} Moltiplicando per \(\cos2\beta\) assume la forma implicita \begin{equation}x\sin 2\beta-y\cos 2\beta+R\sin\beta\cos2\beta-R\cos\beta\sin 2\beta=0.\label{eq:raggioriflesso}\end{equation}
Possiamo ora definire la funzione \begin{equation}F(x,y,\beta)=x\sin 2\beta-y\cos 2\beta+R\sin\beta\cos2\beta-R\cos\beta\sin 2\beta,\end{equation} e calcolare la sua derivata rispetto alla variabile \(\beta\) (in fig. 4.5 utilizziamo le capacità di calcolo simbolico di GeoGebra), \begin{equation}F_\beta(x,y,\beta)=2x\cos 2\beta+2y\sin 2\beta-R\cos\beta\cos2\beta-R\sin\beta\sin2\beta\end{equation} e quindi, coerentemente con quanto sviluppato nelle pagine riguardanti gli inviluppi di curve, le soluzioni del sistema \begin{equation}\cases{F(x,y,\beta)=0\cr F_\beta(x,y,\beta)=0\cr}\end{equation}
Figura 4.5. nefroide05.ggb.
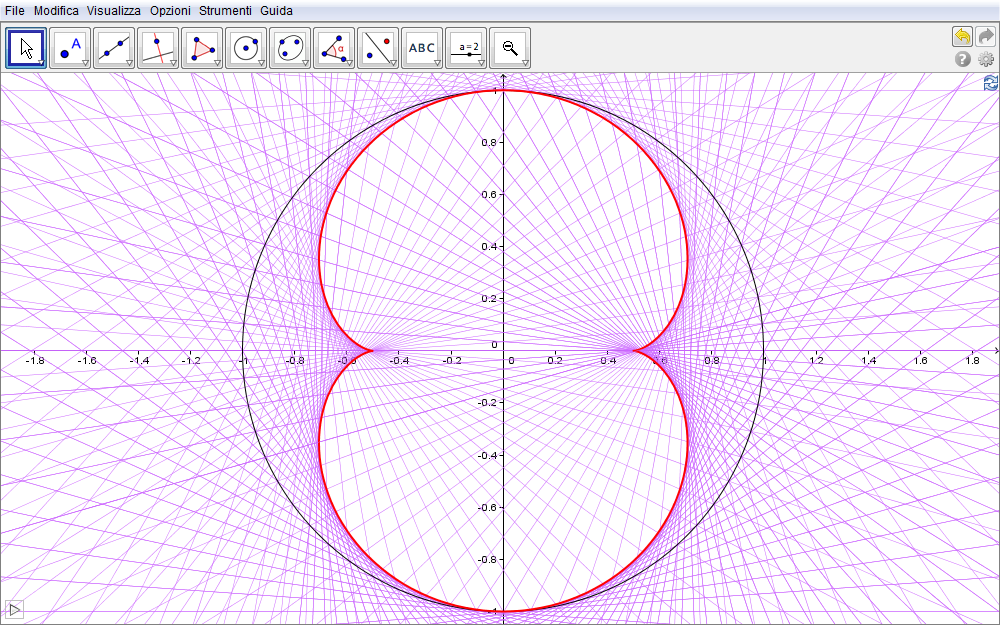
rappresentate dalle \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x={R\over 4}\bigl(3\cos\beta-\cos 3\beta\bigr)\cr\cr y={R\over 4}\bigl(3\sin\beta-\sin3\beta\bigr),\cr}}\label{eq:16}\end{equation} forniscono le equazioni parametriche della curva inviluppo. Difatti le equazioni \eqref{eq:16} coincidono con le \eqref{eq:eqnefroide} non appena si ponga nelle \eqref{eq:16}, \(R=2\), si scambi la x con la y e si sostituisca all'angolo \(\beta\) il suo complementare \({\pi\over 2}-\beta\). La fig. 4.6 mostra il risultato grafico che si ottiene al variare delle rette tangenti.
Figura 4.6. nefroide06.ggb.
Nella figura 4.7 riportiamo in termini un po' più realistici il meccanismo di formazione della caustica di riflessione a seguito dell'incidenza di un fascio di raggi paralleli su uno specchio sferico. Si noti come il fuoco dello specchio coincida con una cuspide della nefroide e, sperimentando con l'animazione, come il raggio riflesso converga con buona approssimazione nel fuoco solo se l'angolo di incidenza dei raggi sullo specchio è prossimo allo zero cioè soddisfi alla approssimazione di Gauss.
Figura 4.7. nefroide07.ggb.
Un secondo inviluppo di rette
Abbiamo concluso la sezione precedente con un esempio di carattere fisico basato sulla legge della riflessione: in quanto segue, ancora con taglio fisico, riprenderemo alcuni elementi di base della cinematica del moto rotatorio e, tramite essi, costruiremo una particolare famiglia di rette il cui inviluppo sarà la nefroide. Per un processo del tutto simile si veda pure la pagina sulla cardioide.
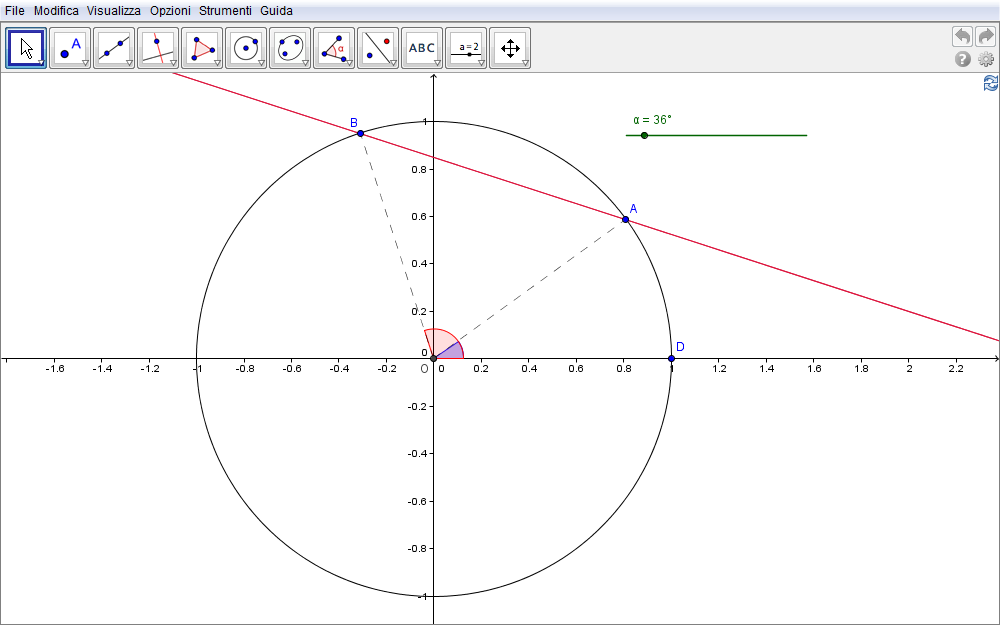
Consideriamo quindi il moto uniforme di un punto A lungo una circonferenza di raggio R (in figura 4.8 scegliamo \(R=1\)). Sappiamo che l'angolo \(\alpha\) percorso in un dato tempo \(t\) è legato a quest'ultimo dalla legge \(\alpha=\omega_A t\) essendo \(\omega_A\) la sua velocità angolare. Sia ora B un secondo punto in moto uniforme sulla medesima circonferenza ma con velocità angolare tripla \(\omega_B=3\omega_A\). Nel medesimo intervallo di tempo l'angolo percorso da B è evidentemente \(\beta=\omega_B t=(3\omega_A)t=3\alpha\) ossia il triplo di \(\alpha\). Con tali presupposti,
- costruita la circonferenza c di centro O e raggio unitario OD (fig. 4.8),
- definiamo uno slider angolare rappresentativo dell'angolo \(\alpha\).
- Con lo strumento Angolo di data misura determiniamo il punto A sulla circonferenza c tale che \(\alpha=\angle(DOA)\). GeoGebra assegna l'etichetta \(\beta\) a quest'angolo ma, non avendo la necessità di visualizzarla, nel seguito continueremo a identificarlo con \(\alpha\).
- Con lo stesso procedimento determiniamo il punto B tale che \(3\alpha=\angle(DOB)\) (è sufficiente scrivere \(3\alpha\) nella finestra che propone GeoGebra) e, infine,
- tracciamo la retta AB.
Figura 4.8. nefroide08.ggb.
Se ora attiviamo la traccia della retta AB al variare dello slider otteniamo la fig. 4.9 dalla quale appare evidente come l'inviluppo di tale famiglia sia la nefroide.
Figura 4.9. nefroide09.ggb.
Per la dimostrazione dobbiamo scrivere l'equazione di tale famiglia in termini di un parametro che, per come si sono costruiti i punti A e B non può che essere l'angolo \(\alpha=\angle(DOA)\) (fig. 4.8). Le coordinate di A sono pertanto \(A(R\cos\alpha,R\sin\alpha)\) per cui, tenendo presente che \(\beta=3\alpha\) quelle di B sono \(B(R \cos 3\alpha, R \sin 3\alpha)\). Osservato che il coefficiente angolare della retta AB è \begin{equation}m_{AB}={y_B-y_A\over x_B-x_A}={R \sin 3\alpha-R\sin\alpha\over R\cos 3\alpha-R\cos\alpha}={\sin 3\alpha-\sin\alpha\over \cos 3\alpha-\cos\alpha},\end{equation} la retta ha equazione \begin{equation}y-y_A=m_{AB}(x-x_A)\qquad y-R\sin\alpha={\sin 3\alpha-\sin\alpha\over \cos 3\alpha-\cos\alpha}\cdot (x-R\cos\alpha)\end{equation} e in forma implicita \begin{equation}(\cos3\alpha-\cos\alpha)(y-R\sin\alpha)=(\sin3\alpha-\sin\alpha)(x-R\cos\alpha).\end{equation} Quest'ultima scrittura ci permette di introdurre la funzione implicita \begin{equation}F(x,y,\alpha)=(\cos3\alpha-\cos\alpha)(y-R\sin\alpha)-(\sin3\alpha-\sin\alpha)(x-R\cos\alpha),\end{equation} dalla quale ottenere, tramite il calcolo simbolico di GeoGebra (fig. 4.10), la sua derivata parziale prima rispetto a \(\alpha\) \begin{equation}F_\alpha(x,y,\alpha)=x\cos\alpha-3x\cos3\alpha+y\sin\alpha-3y\sin3\alpha+2R\cos\alpha\cos3\alpha+2R\sin\alpha\sin3\alpha.\end{equation}
Figura 4.10. nefroide10.ggb.
Sappiamo che la coppia soluzione del sistema (di I grado) \begin{equation}\cases{F(x,y,\alpha)=0\cr F_\alpha(x,y,\alpha)=0\cr}\end{equation} rappresenta parametricamente la curva inviluppo: in tal caso GeoGebra fornisce \begin{equation}\cases{x=R\cos^3\alpha\cr y= -R\sin^3\alpha+{3\over 2}R\sin\alpha.\cr}\label{eq:25}\end{equation} Poiché comunque valgono le identità goniometriche \begin{equation}\cos 3\alpha=4\cos^3\alpha-3\cos\alpha,\qquad \sin3\alpha=3\sin\alpha-4\sin^3\alpha,\end{equation} dalle quali discende la coppia \begin{equation}\cos^3\alpha={1\over 4}\bigl(\cos3\alpha+3\cos\alpha\bigr),\qquad \sin^3\alpha=-{1\over 4}\bigl(\sin 3\alpha-3\sin\alpha\bigr),\label{eq:identitaCub}\end{equation} che sostituita in \eqref{eq:25} ci permette di scrivere \begin{equation}\cases{x={R\over 4}\bigl(3\cos \alpha+\cos 3\alpha\bigr)\cr\cr y={R\over 4}\bigl(3\sin\alpha+\sin3\alpha\bigr),\cr}\end{equation} equazioni del tutto simili alle \eqref{eq:eqnefroide} non appena si consideri il rapporto di scala esistente tra le due costruzioni.
Per una generalizzazione di quanto qui esposto si consulti ancora la pagina relativa alla curva cardioide.
Un inviluppo di circonferenze
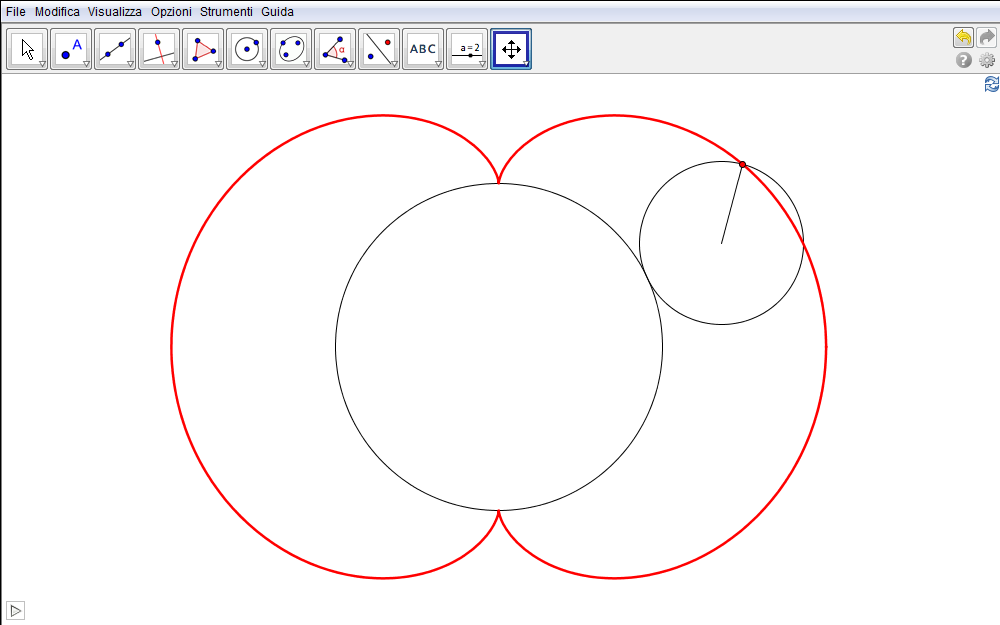
Nelle ultime sezioni abbiamo ottenuto la nefroide a partire da due diverse famiglie di rette ad essa tangenti. Qui invece intendiamo ottenerla ancora come inviluppo ma a partire da una famiglia di circonferenze. Con tale obiettivo,
- costruita la circonferenza c di centro A, origine di un sistema cartesiano, e raggio R (in fig. 4.11 è \(R=1\)),
- definito uno slider angolare \(\alpha\),
- individuare il punto C della circonferenza tale che \(\angle(BAC)=\alpha\). A tale scopo va utilizzato lo strumento Angolo di data misura.
- Tracciate quindi le rette coordinate passanti per C,
- siano, rispettivamente, D ed E le loro intersezioni con gli assi y e x.
- Costruire infine la circonferenza di centro C e raggio CD, evidentemente tangente all'asse y.
Figura 4.11. nefroide11.ggb.
Attivata la traccia per quest'ultima circonferenza al variare dello slider, emerge con evidenza la forma della nefroide (fig. 4.12).
Figura 4.12. nefroide12.ggb.
Dimostrazione. Poiché le coordinate di C sono \(C(R\cos\alpha,R\sin\alpha)\), il raggio della famiglia di circonferenze di centro C e tangenti all'asse y è pari a \(CD=AE=\bigl|x_C\bigr|=\bigl|\,R \cos\alpha\,\bigr|\). Ne segue che l’equazione della famiglia è \begin{equation}(x-R\cos\alpha)^2+(y-R\sin\alpha)^2=(R\cos\alpha)^2\label{eq:famiglia}\end{equation} e la funzione che ne deriva trasportando tutti i termini a primo membro è \[F(x,y,\alpha)=(x-R\cos\alpha)^2+(y-R\sin\alpha)^2-(R\cos\alpha)^2.\] Il calcolo della sua derivata parziale rispetto a \(\alpha\) fornisce (in fig. 4.13 riportiamo quanto si ottiene nella vista CAS di GeoGebra)\[F_\alpha(x,y,\alpha)=2\,R\,x\sin\alpha-2\,R\,y\cos\alpha+2R^2\sin\alpha\cos\alpha\]
Figura 4.13. nefroide13.ggb.
e le soluzioni del sistema (di II grado) \begin{equation}\cases{F(x,y,\alpha)=0\cr F_\alpha(x,y,\alpha)=0\cr}\end{equation} sono \begin{equation}\cases{x=2R\cos^3\alpha\cr y=3R\sin\alpha-2R\sin^3\alpha,\cr}\qquad\hbox{e}\qquad \cases{x=0\cr y=R\sin\alpha.\cr}\end{equation} La prima coppia si riduce facilmente alle \eqref{eq:eqnefroide} se si considerano le identità \eqref{eq:identitaCub}, mentre la seconda descrive nient'altro che il segmento dell'asse y pure esso tangente alla famiglia \eqref{eq:famiglia}.
La nefroide come luogo
Concludiamo la nostra presentazione della nefroide proponendo direttamente la costruzione di un suo punto evitando quindi osservazioni sul moto di un punto o altri "meccanismi" di carattere fisico.
- Costruita pertanto una circonferenza centrata sull'origine A e di raggio \(AB=R\) (in fig. 4.14 è \(AB=1\)),
- definiamo uno slider angolare \(\alpha\) e quindi
- determiniamo sulla circonferenza, tramite lo strumento Angolo di data misura il punto C tale che \(\angle(BAC)=\alpha\) e
- tracciamo pure il segmento AC.
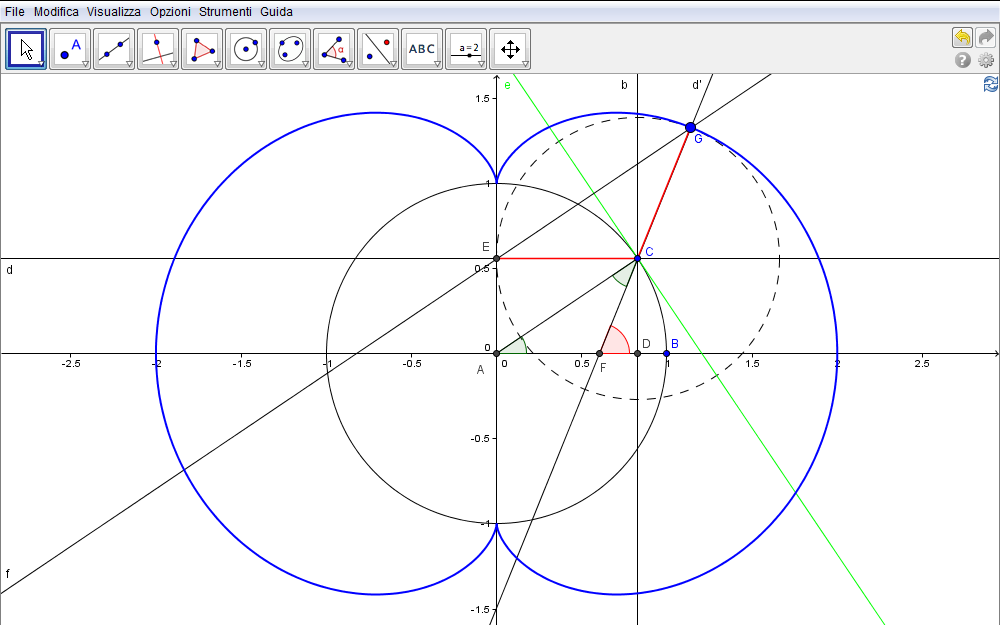
- Costruita la retta e tangente in C alla circonferenza,
- siano D ed E le proiezioni di C sugli assi cartesiani rispettivamente su x e y.
- Tramite lo strumento Simmetria assiale, ottenere la retta d' per C, simmetrica della retta EC rispetto alla tangente e, e quindi
- tracciata la retta per E parallela al segmento AC,
- sia G l'intersezione di quest'ultima retta con d'.
Figura 4.14. nefroide14.ggb.
Lo strumento Luogo di G al variare dello slider permette infine di visualizzare la nefroide come mostrato dalla fig. 4.15.
Figura 4.15. nefroide15.ggb.
Per la dimostrazione dovremo evidentemente determinare le coordinate del punto G in termini dell'angolo \(\alpha=\angle(BAC)\), parametro che coincide con quello introdotto all'inizio di questa pagina per cui ci aspettiamo come risultato le equazioni \eqref{eq:eqnefroide}.
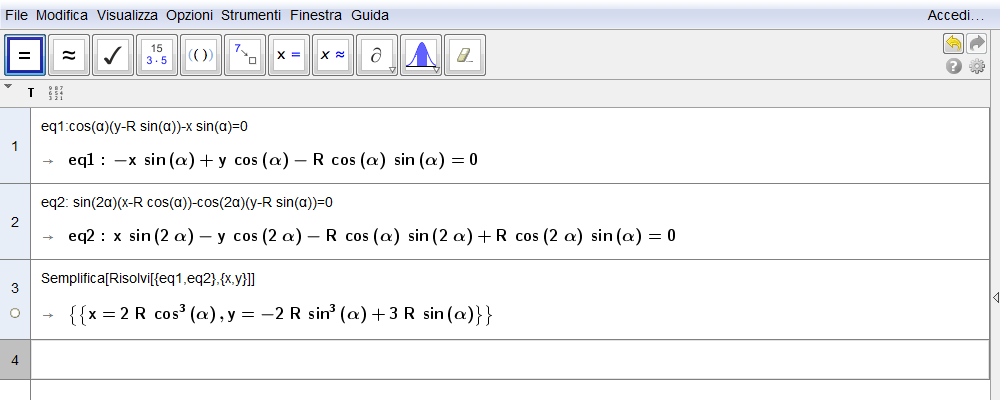
Poiché le coordinate di C sono \(C(R \cos\alpha,R\sin\alpha)\) e il coefficiente angolare di AC è \(m_{AC}=\sin\alpha\,/\cos\alpha\), l'equazione della retta EG, parallela ad AC e passante per \(E(0,R\sin\alpha)\), è \begin{equation}EG: y-R\sin\alpha= \biggl(\!{\sin\alpha\over\cos\alpha}\!\biggr)\,x\quad\hbox{e in forma implicita}\quad \cos\alpha\bigl(y-R\sin\alpha\bigr)-x\sin\alpha=0.\label{eq:31}\end{equation} L'angolo \(\angle(BFC)\) che la retta per C fa invece con l'asse x (fig. 4.15), è adiacente esterno a \(\triangle(AFC)\) per cui \begin{equation}\angle(BFC)=\angle(FAC)+\angle(ACF)\label{eq:32}\end{equation} ma la simmetria assiale della retta CG con la retta CE implica pure la simmetria assiale di queste rette anche rispetto al raggio AC in quanto quest'ultimo è perpendicolare alla retta tangente. Segue quindi \(\angle(ACE)=\angle(ACF)\) e, tenuto conto della congruenza tra angoli alterni interni, risulta \begin{equation}\alpha=\angle(BAC)=\angle(FAC)=\angle(ACE)=\angle(ACF)\end{equation} cosicché la \eqref{eq:32} diviene \begin{equation}\angle(BFC)=\alpha+\alpha=2\alpha.\end{equation} La retta CG ha quindi equazione \begin{equation}CG: y-y_C=m_{CG}(x-x_C)\qquad y -R\sin\alpha=\tan(\angle BFC)(x-R\cos\alpha)\end{equation} e, considerato che \(\tan(\angle BFC)=\tan2\alpha=\sin2\alpha\,/\cos2\alpha\), in forma implicita è \begin{equation}\sin2\alpha\bigl(x-R\cos\alpha\bigr)-\cos 2\alpha\bigl(y-R\sin\alpha\bigr)=0.\end{equation} Notiamo come questa equazione coincida con la \eqref{eq:raggioriflesso} ottenuta nella costruzione della nefroide come caustica di riflessione.
La soluzione del sistema (di I grado) tra la \eqref{eq:31} e la precedente \begin{equation}\cases{\cos\alpha\bigl(y-R\sin\alpha\bigr)-x\sin\alpha=0\cr \sin2\alpha\bigl(x-R\cos\alpha\bigr)-\cos 2\alpha\bigl(y-R\sin\alpha\bigr)=0\cr}\end{equation} fornisce le coordinate del punto G appartenente alla nefroide. Utilizzando la vista CAS di GeoGebra (fig. 4.16) deduciamo \begin{equation}\cases{x=2R\cos^3\alpha\cr y=3R\sin\alpha-2R\sin^3\alpha\cr}\end{equation} che, come già visto, con le identità \eqref{eq:identitaCub} si riducono facilmente alle \eqref{eq:eqnefroide}.
Figura 4.16. nefroide16.ggb.
In conclusione, aggiungiamo nella figura 4.15 la circonferenza di centro C e raggio CE così da collegare quest'ultima costruzione alla precedente: è ora evidente come il punto G qui individuato sia pure il punto di tangenza tra le circonferenze della famiglia \eqref{eq:famiglia} e la nefroide.