La cardioide
- Note storiche
- La cardioide come epicicloide
- Cardioide come inviluppo di circonferenze
- Equazione polare della cardioide
- Un inviluppo di rette
- Caustica di riflessione
- Costruzione di un punto
Note storiche
Il nome di cardioide che significa a forma di cuore fu introdotto da Giovanni Francesco Salvemini detto il Castiglione (o anche Johann Castillon) in un articolo scritto in latino pubblicato nelle Philosophical Transactions of the Royal Society nel 1741. Nello studio di tale curva era comunque stato preceduto già nel 1708 da Philippe de La Hire che ne aveva determinato la lunghezza.
La cardioide come epicicloide
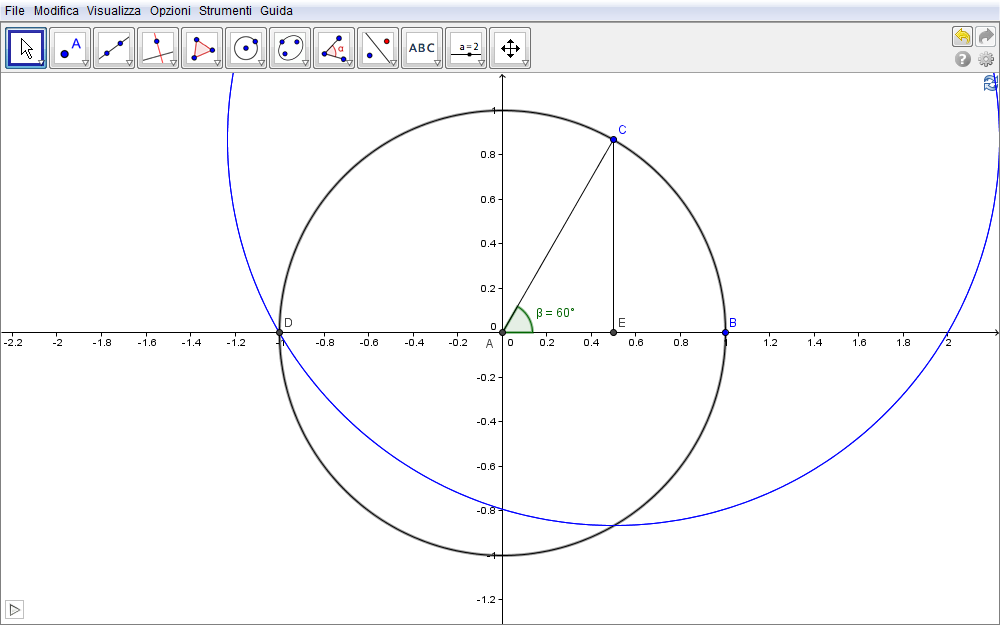
Abbiamo già introdotto la curva cardioide trattandola come un caso particolare di epicicloide. Difatti se il raggio del cerchio mobile è uguale a quello del cerchio fisso, un punto sul primo genera tale curva: nella animazione di fig. 5.1 compaiono, in aggiunta al punto sulla cardioide pure il centro e un raggio del cerchio in rotazione.
Figura 5.1. cardioide01.ggb.
Le sue equazioni rappresentative si ricavano da quelle di una epicicloide non appena si ponga \(R=r\) e sono \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x=R\bigl(2\cos\beta+\cos 2\beta\bigr)\cr y=R\bigl(2\sin\beta+\sin2\beta\bigr)}}\label{eq:1}\end{equation} dove \(\beta\) rappresenta l'angolo che ha per lati l'asse x e la semiretta uscente dall'origine e passante per il punto di contatto dei due cerchi (fig. 4.1).
Cardioide come inviluppo di circonferenze
La cardioide si può ottenere in diversi altri modi: quello che qui proponiamo si basa sulla definizione di inviluppo per la quale rimandiamo alla pagina dove presentiamo il metodo che permette di giungere alle equazioni rappresentative. Qui basta ricordare che, costruita una famiglia di curve dipendente da un parametro per inviluppo si intende
una curva che sia tangente in qualche punto ad ogni membro di una data famiglia di curve.
Figura 5.2. cardioide02.ggb.
Consideriamo quindi
- una circonferenza di raggio \(AB=R=1\) centrata nell'origine A di un sistema cartesiano (fig. 5.2) e,
- definito uno slider angolare \(\alpha\),
- sia C il punto della circonferenza tale che \(\angle(BAC)=\alpha\) (GeoGebra indica con \(\beta\) tale angolo). Lo strumento da utilizzare è Angolo di data misura,
 ).
). - Se \(D(-1,0)\) è l'estremo opposto a B del diametro della circonferenza,
- sia d la circonferenza di centro C e raggio CD.
Al variare di C sulla circonferenza originaria, la cardioide emerge come l'inviluppo della famiglia d (fig. 5.3).
Volendo ritrovare le equazioni rappresentative con il metodo degli inviluppi, scriviamo l'equazione della famiglia di circonferenze d.
Figura 5.3. cardioide03.ggb.
Poiché le coordinate di C sono, in termini di \(\beta\), \(C(R\cos\beta,R\sin\beta)\), il quadrato del raggio \(CD\) è \[CD^2=(x_C+R)^2+y_C^2= (R\cos\beta+R)^2+R^2\sin^2\beta\] per cui l'equazione della famiglia di circonferenze risulta \begin{equation}(x-R\cos\beta)^2+(y-R\sin\beta)^2=(R\cos\beta+R)^2+R^2\sin^2\beta\end{equation} che riscriviamo come \begin{equation}d:(x-R\cos\beta)^2+(y-R\sin\beta)^2-(R\cos\beta+R)^2-R^2\sin^2\beta=0.\end{equation} Possiamo ora definire la funzione \begin{equation}F(x,y,\beta)=(x-R\cos\beta)^2+(y-R\sin\beta)^2-(R\cos\beta+R)^2-R^2\sin^2\beta\label{eq:4}\end{equation} e, su tale base, calcolare la sua derivata parziale rispetto al parametro \(\beta\), \(F_\beta(x,y,\beta)\), (in fig. 5.4 sfruttiamo le capacità di calcolo simbolico di GeoGebra) \begin{equation}F_\beta(x,y,\beta)=2R^2\sin\beta+2Rx\sin\beta-2Ry\cos\beta.\label{eq:5}\end{equation}
Figura 5.4. cardioide04.ggb.
Impostato il sistema di II grado tra \eqref{eq:4} e \eqref{eq:5}\begin{equation}\cases{F(x,y,\beta)=0\cr F_\beta(x,y,\beta)=0,\cr}\end{equation} l'unica soluzione significativa è data dalla coppia \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x=R\bigl(2\cos^2\beta-1+2\cos\beta\bigr)\cr y=R\bigl(2\sin\beta\cos\beta+2\sin\beta\bigr)\cr}}\end{equation} che, per le note formule di duplicazione, è manifestamente identica alla coppia di equazioni parametriche \eqref{eq:1}.
Equazione polare della cardioide
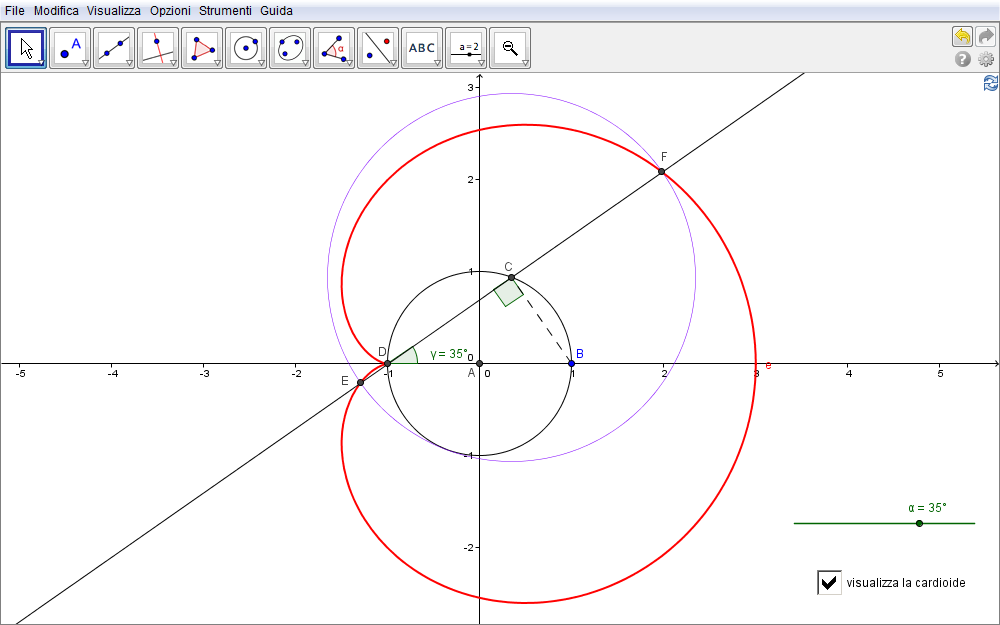
Nella pagina riguardante la concoide di Nicomede abbiamo fornito pure la procedura generale per costruire una curva concoide a partire da un punto scelto come polo e da una curva base che, in quel contesto, era nient'altro che una retta. In questa sezione vogliamo riprendere un tale procedimento scegliendo come curva base la circonferenza di raggio \(AB=R\) (unitario in fig. 5.5) delle sezioni precedenti e come polo il suo punto D (fig. 5.5).
Figura 5.5. cardioide05.ggb.
- Definito lo slider angolare \(\alpha\) con valori in \([-90°,90°]\) e
- costruito il punto C della circonferenza tale che sia \(\angle(ADC)=\gamma=\alpha\),
- sia DC la retta per questi due punti.
- Con centro in C tracciamo la circonferenza di raggio pari a \(2R\), circonferenza che evidentemente sarà tangente a quella iniziale nel punto del diametro opposto a C.
- Siano E ed F i punti di intersezione di questa circonferenza con la retta DC.
Al variare di \(\alpha\) il luogo di questi due punti è la cardioide. Per la dimostrazione di carattere algebrico di tale affermazione dovremmo innanzitutto determinare:
- l'equazione della famiglia di circonferenze di centro \(C(R \cos2\gamma,R\sin2\gamma)\) e raggio \(2R\). Tenuto conto che \(\angle(BAC)=2\gamma\), questo è \begin{equation}(x-R\cos2\gamma)^2+(y-R\sin2\gamma)^2=(2R)^2.\label{eq:famigliacfr}\end{equation}
- L'equazione della retta CD e passante per \(C\), \[x\sin2\gamma-y\cos 2\gamma -y + R\sin 2\gamma=0\]
- e quindi ricondurre le soluzioni del sistema di II grado \[\cases{(x-R\cos2\gamma)^2+(y-R\sin2\gamma)^2=4R^2\cr x \sin2\gamma-y \cos 2\gamma -y + R\sin 2\gamma=0}\]
alle già note equazioni \eqref{eq:1} tenendo conto che \(2\gamma=\beta\). Qui preferiamo invece, per l'immediatezza delle osservazioni, determinare le coordinate dei due punti E ed F inizialmente in un sistema polare con polo in D e coordinata angolare (o anomalia) pari all'angolo \(\gamma\): solo in un secondo momento dedurremo le equazioni rappresentative.
Se osserviamo la figura 5.5, la coordinata radiale (o modulo) \(\rho_F\) è determinata dalla lunghezza del segmento \(DF\) per cui possiamo scrivere \(\rho_F=DF=DC+CF\). D'altra parte \(DC=BD\cos(\angle BDC)=2R\cos\gamma\) e, per costruzione \(CF=2R\). Pertanto F in un tale sistema polare è identificato dalla relazione \[\rho_F=2R+2R\cos\gamma=2R(1+\cos\gamma).\] Analogamente per il punto E abbiamo \[\rho_E=EC-DC=2R-2R\cos\gamma=2R(1-\cos\gamma)\] per cui, estendendo l'intervallo dell'angolo \(\gamma\), la funzione \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\rho=2R(1+\cos\gamma)\qquad \gamma\in[0,2\pi]}\label{eq:8}\end{equation} rappresenta la cardioide nel sistema polare scelto.
Per riportare questo risultato alle coordinate cartesiane dobbiamo considerare la coppia di equazioni \begin{equation}\cases{x'=\rho\cos\gamma\cr y'=\rho\sin\gamma\cr}\label{eq:9}\end{equation} che collega le coordinate cartesiane con quelle polari ma nel caso in cui il polo coincida con l'origine del sistema cartesiano. Poiché il polo scelto ha coordinate cartesiane \(D(-R,0)\) le \eqref{eq:9} vanno integrate con la traslazione \[\cases{x=x'-R\cr y=y'}\] cosicché dev'essere \[\cases{x=\rho\cos\gamma-R\cr y=\rho\sin\gamma.\cr}\] Sostituiamo la \eqref{eq:8} nelle precedenti \begin{equation}\cases{x=2R(1+\cos\gamma)\cos\gamma-R\cr y=2R(1+\cos\gamma)\sin\gamma,\cr}\end{equation} e, con le formule goniometriche di duplicazione, deduciamo infine le \begin{equation}\cases{x=2R\cos\gamma+R(2\cos^2\gamma-1)=R\bigl(2\cos\gamma+\cos2\gamma\bigr)\cr y=2R\sin\gamma+2R\cos\gamma\sin\gamma=R\bigl(2\sin\gamma+\sin2\gamma\bigr)\cr}\end{equation} che coincidono con la coppia \eqref{eq:1}. La fig. 5.6 riporta la cardioide assieme alle circonferenze del famiglia \eqref{eq:famigliacfr}: ripresa la nota iniziale, questa figura conferma visivamente come la cardioide si possa considerare una concoide di una circonferenza di raggio R rispetto ad un suo punto scelto come polo e generata da una famiglia di circonferenze con il diametro di lunghezza 2R.
Figura 5.6. cardioide06.ggb.
Un inviluppo di rette
La cardioide si può ottenere come inviluppo, non solo costruendo una famiglia di circonferenze come già visto in questa pagina ma pure tramite una famiglia di rette. Per ottenere tale famiglia ricorriamo, inizialmente, ad osservazioni di carattere cinematico, facilmente generalizzabili e del tutto simili a quanto esposto sulla nefroide.
Consideriamo quindi il moto uniforme di un punto A lungo una circonferenza di raggio R (in figura 5.7 scegliamo \(R=1\)). Sappiamo che l'angolo \(\alpha\) percorso in un dato tempo \(t\) è legato a quest'ultimo dalla legge \(\alpha=\omega_A t\) essendo \(\omega_A\) la sua velocità angolare. Sia ora B un secondo punto in moto uniforme sulla medesima circonferenza ma con velocità angolare doppia \(\omega_B=2\omega_A\). Nel medesimo intervallo di tempo l'angolo percorso da B è evidentemente \(\beta=\omega_B t=(2\omega_A)t=2\alpha\) ossia il doppio di \(\alpha\). Con tali presupposti,
- costruita la circonferenza c di centro A e raggio unitario AB (fig. 5.7),
- definiamo uno slider angolare rappresentativo dell'angolo \(\alpha\).
- Con lo strumento Angolo di data misura determiniamo il punto C sulla circonferenza c tale che \(\alpha=\angle(BAC)\). GeoGebra assegna l'etichetta \(\beta\) a quest'angolo ma, non avendo la necessità di visualizzarla, nel seguito continueremo a identificarlo con \(\alpha\).
- Con lo stesso procedimento determiniamo il punto D tale che \(2\alpha=\angle(BAD)\): è sufficiente scrivere \(2\alpha\) nella finestra proposta da GeoGebra una volta che si sia scelto lo strumento Angolo di data misura e, infine,
- tracciamo la retta CD.
Figura 5.7. cardioide07.ggb.
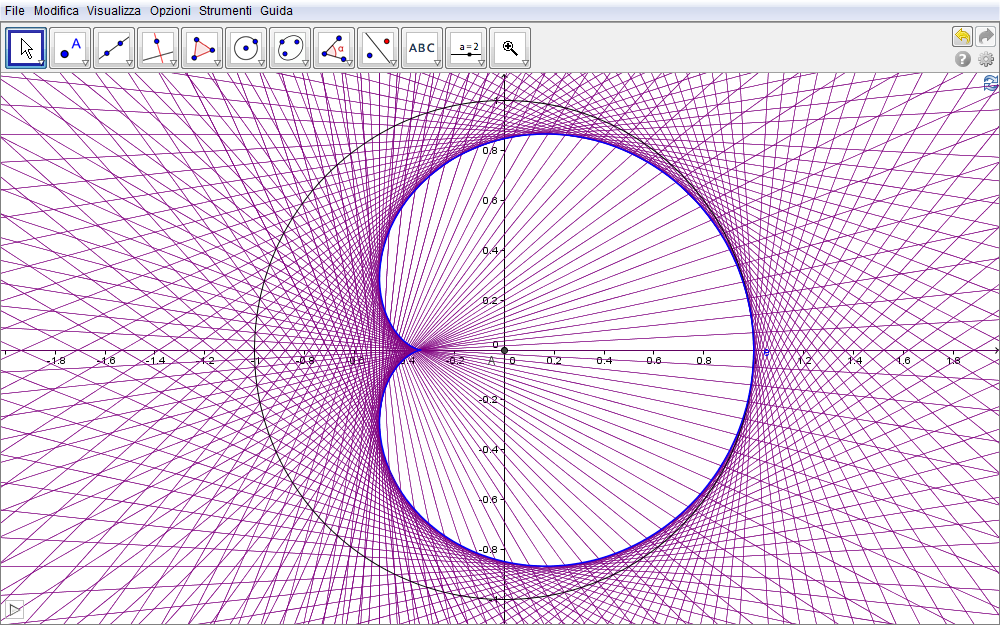
Se ora attiviamo la traccia della retta CD al variare dello slider otteniamo la fig. 5.8 dalla quale appare evidente come l'inviluppo di tale famiglia sia la curva aspettata ma con un rapporto di scala pari ad 1/3 rispetto alle costruzioni finora presentate.
Figura 5.8. cardioide08.ggb.
Per la dimostrazione dobbiamo scrivere l'equazione della famiglia di rette in termini di un parametro che, per come si sono costruiti i punti C e D non può che essere l'angolo \(\alpha=\angle(BAC)\) (fig. 5.7). Le coordinate di C sono pertanto \(C(R\cos\alpha,R\sin\alpha)\) per cui, tenendo presente che \(\angle(BAD)=2\alpha\) quelle di D sono \(D(R \cos 2\alpha, R \sin 2\alpha)\). Osservato che il coefficiente angolare della retta CD è \begin{equation}m_{CD}={y_D-y_C\over x_D-x_C}={R \sin 2\alpha-R\sin\alpha\over R\cos 2\alpha-R\cos\alpha}={\sin 2\alpha-\sin\alpha\over \cos 2\alpha-\cos\alpha},\end{equation} la retta ha equazione \begin{equation}y-y_C=m_{CD}(x-x_C)\qquad y-R\sin\alpha={\sin 2\alpha-\sin\alpha\over \cos 2\alpha-\cos\alpha}\cdot (x-R\cos\alpha)\end{equation} e in forma implicita \begin{equation}(\cos2\alpha-\cos\alpha)(y-R\sin\alpha)=(\sin2\alpha-\sin\alpha)(x-R\cos\alpha).\end{equation} Quest'ultima scrittura ci permette di introdurre la funzione implicita \begin{equation}F(x,y,\alpha)=(\cos2\alpha-\cos\alpha)(y-R\sin\alpha)-(\sin2\alpha-\sin\alpha)(x-R\cos\alpha),\end{equation} dalla quale ottenere, tramite il calcolo simbolico di GeoGebra (fig. 5.9), la sua derivata parziale prima rispetto a \(\alpha\) \begin{equation}F_\alpha(x,y,\alpha)=x\cos\alpha-2x\cos2\alpha+y\sin\alpha-2y\sin2\alpha+R\cos\alpha\cos2\alpha+R\sin\alpha\sin2\alpha.\end{equation}
Figura 5.9. cardioide09.ggb.
Sappiamo che la coppia soluzione del sistema (di I grado) \begin{equation}\cases{F(x,y,\alpha)=0\cr F_\alpha(x,y,\alpha)=0\cr}\end{equation} rappresenta parametricamente la curva inviluppo: GeoGebra fornisce (fig. 5.9)\begin{equation}\cases{x={R\over 3}\bigl(2\cos^2\alpha+2\cos\alpha-1\bigr)\cr\cr y= {R\over 3}\bigl(2\sin\alpha\cos\alpha+2\sin\alpha\bigr).\cr}\label{eq:18}\end{equation} Le formule di duplicazione ci permettono di scrivere \begin{equation}\cases{x={R\over 3}\bigl(2\cos \alpha+\cos 2\alpha\bigr)\cr\cr y={R\over 3}\bigl(2\sin\alpha+\sin2\alpha\bigr),\cr}\label{eq:20}\end{equation} equazioni del tutto simili alle \eqref{eq:1} non appena si consideri il rapporto di scala esistente tra le due costruzioni.
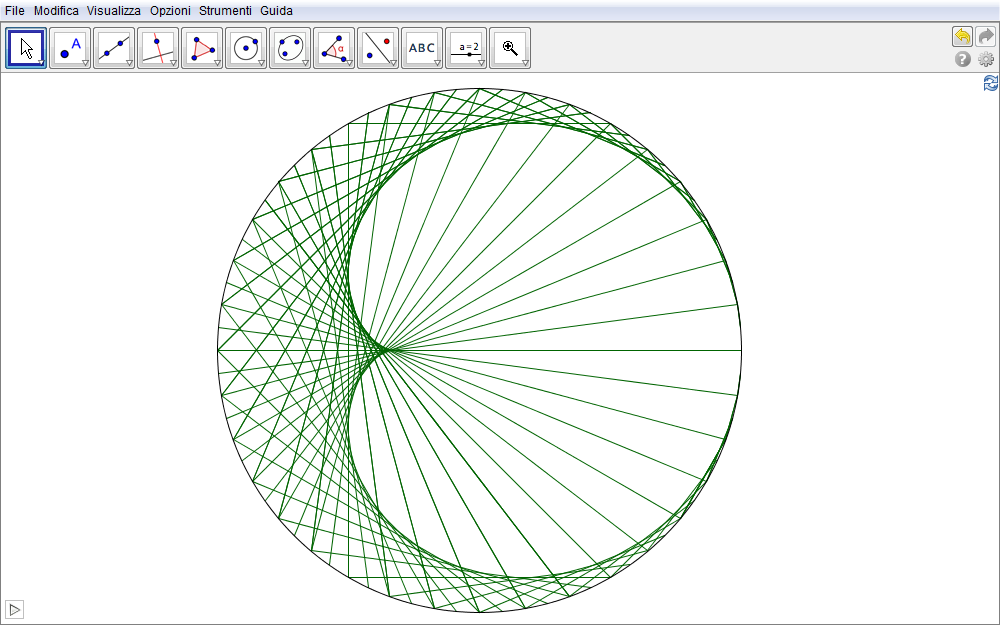
Se in alternativa alla retta CD tracciamo il solo segmento CD otteniamo come immagine un logo ben conosciuto a molti studenti, quello delle Olimpiadi della Matematica (fig. 5.10).
Figura 5.10. cardioide10.ggb.
Infine, il metodo qui presentato è, ovviamente, facilmente generalizzabile: un primo esempio è la curva nefroide, dove il secondo punto sulla circonferenza si muove lungo la circonferenza con velocità tripla rispetto al primo. Se quest'ultima è invece quattro volte maggiore si ottiene la curva di fig. 5.11
Figura 5.11. cardioide11.ggb.
le cui equazioni rappresentative sono \[\cases{x={R\over 5}\bigl(4\cos\alpha+\cos4\alpha\bigr)\cr\cr y={R\over 5}\bigl(4\sin\alpha+\sin4\alpha\bigr).\cr}\] Infine, l'animazione di figura 5.12 mostra, in successione, le diverse curve inviluppo associate ai rapporti (di velocità) \(1\leq n\leq 10\): appare evidente come il numero di cuspidi sia pari a \(n-1\).
Figura 5.12. cardioide12.ggb.
Caustica di riflessione
La curva nefroide si può ottenere come inviluppo di una famiglia di raggi riflessi da uno specchio sferico quando su questo incida un fascio di raggi paralleli. In questa sezione otterremo invece la cardioide come inviluppo di raggi riflessi, sempre da uno specchio sferico, ma provenienti da un punto appartenente alla circonferenza dello specchio. In ogni caso, le curve che si ottengono in tal modo, si dicono caustiche di riflessione.
Figura 5.13. cardioide13.ggb.
- Tracciamo la circonferenza di raggio \(AB=R\) (unitario in fig. 5.13) con centro nell'origine A di un sistema cartesiano e
- definiamo lo slider angolare \(\alpha\)
- rappresentativo dell'angolo al centro \(\beta=\angle(BAC) (=\alpha)\).
- Sia quindi D il punto della circonferenza di coordinate \(D(-R,0)\) e,
- costruita la retta \(a=DC\) e
- il segmento AC, sia
- b la retta simmetrica rispetto al raggio AC. Per ottenerla utilizzare lo strumento Simmetria assiale, selezionando dapprima la retta DC e quindi il raggio AC.
- Sia E il punto di intersezione di quest'ultima retta con l'asse x.
Evidentemente per costruzione si ha \(\angle(ACD)=\angle(ACE)\) per cui il raggio uscente da C si può considerare come il raggio riflesso del raggio DC uscente dal punto fisso D. Per determinare l'equazione della retta CE dobbiamo determinare l'angolo che questa definisce con l'asse x cioè \(\angle(BEC)\). Pertanto considerando che questo è adiacente esterno del triangolo EDC \begin{equation}\angle(BEC)=\angle(EDC)+\angle(DCE).\label{eq:21}\end{equation} Ma \begin{equation}\angle(EDC)={1\over 2}\angle(BAC)={1\over 2}\beta\end{equation} in quanto \(\angle(EDC)\) è angolo alla circonferenza corrispondente all'angolo al centro \(\angle(BAC)=\beta\). Poichè inoltre \(\angle(EDC)=\angle(ACD)=\angle(ACE)\) essendo \(\triangle(ACD)\) isoscele, è pure \begin{equation}\angle(DCE)=2\angle(EDC)=\beta\end{equation} e dalla \eqref{eq:21} segue che \begin{equation}\angle(BEC)={1\over 2}\beta+\beta={3\over 2}\beta.\end{equation} Il coefficiente angolare della retta CE risulta \begin{equation}m_{CE}=\tan(\angle BEC)=\tan\biggl(\!{3\over 2}\beta\!\biggr)\end{equation} e la retta cercata è, nella forma esplicita, \begin{equation}CE:y-y_C=m_{CE}(x-x_C)\quad\Longrightarrow\quad y-R\sin\beta=\tan\biggl(\!{3\over 2}\beta\!\biggr)\bigl(x-R\cos\beta\bigr).\end{equation} Quest'ultima ci permette di definire la funzione \begin{equation}F(x,y,\beta)=y-R\sin\beta-\tan\biggl(\!{3\over2}\beta\!\biggr)\bigl(x-R\cos\beta\bigr)\end{equation} e, coerentemente con il metodo già descritto, calcolare la sua derivata prima rispetto alla sola variabile \(\beta\). Tramite la vista CAS di GeoGebra, la soluzione del sistema di I grado \begin{equation}\cases{F(x,y,\beta)=0\cr F_\beta(x,y,\beta)=0\cr}\end{equation} è la coppia di equazioni
Figura 5.14. cardioide14.ggb.
\begin{equation}\cases{x={R\over 3}\bigl(2\cos\beta-2\cos^2\beta+1\bigr)={R\over 3}\bigl(2\cos\beta-\cos2\beta\bigr)\cr\cr y={R\over 3}\bigl(2\sin\beta-2\cos\beta\sin\beta\bigr)={R\over 3}\bigl(2\sin\beta-\sin2\beta\bigr)\cr}\end{equation} che rientrano nella forma \eqref{eq:20} se si considera la simmetria assiale rispetto all'asse y e il fatto che \(\beta=\pi-\alpha\) essendo \(\alpha\) l'angolo utilizzato nelle \eqref{eq:20}. In fig. 5.15 l'inviluppo appena discusso.
Figura 5.15. cardioide15.ggb.
Costruzione di un punto
In quest'ultima sezione costruiremo direttamente un punto P della cardioide con i soli strumenti geometrici evitando quindi sia "contaminazioni" di carattere fisico, sia il concetto di inviluppo.
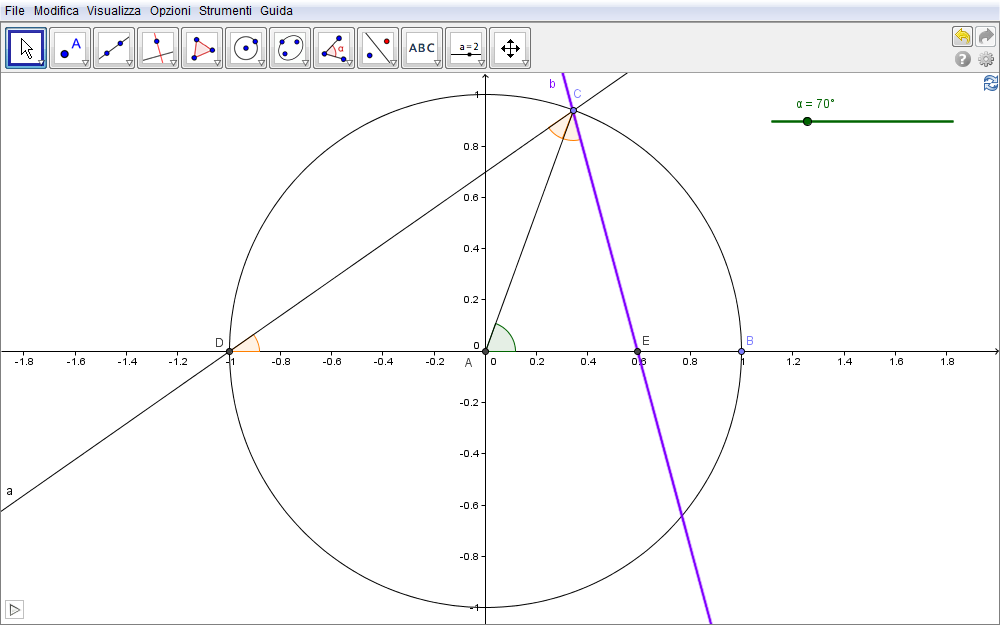
Come nella precedente sezione, partiamo quindi da una circonferenza di centro A e raggio \(AB=R\) e dal solito slider angolare \(\alpha\), tramite il quale definire l'angolo \(\angle(BAC)=\beta=\alpha\).
- Tracciato il raggio AC,
- costruiamo la retta b tangente alla circonferenza in C.
- Se D è un punto della circonferenza (nella fig. 5.16 lo scegliamo di coordinate \(D(-R,0)\)),
- il punto P, simmetrico di D rispetto alla retta tangente, è il punto appartenente alla cardioide.
Figura 5.16. cardioide16.ggb.
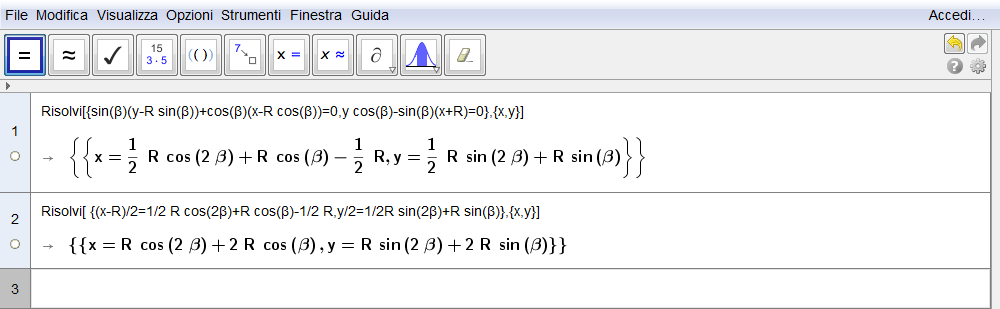
Per dimostrarlo dovremo determinare le coordinate di P in termini dell'angolo \(\beta\): a tale scopo intendiamo determinare l'equazione della retta tangente nel sistema cartesiano di origine A. Poiché \(C(R\cos\beta, R\sin\beta)\), il coefficiente angolare di AC è \(m_{AC}=\tan\beta\) per cui la retta b ha equazione \begin{equation}b: y-y_C=-{1\over m_{AC}}(x-x_C)\quad\Longrightarrow\quad y-R\sin\beta=-{\cos\beta\over\sin\beta}\bigl(x-R\cos\beta\bigr),\end{equation} e in forma implicita \begin{equation}\sin\beta\bigl(y-R\sin\beta\bigr)+\cos\beta\bigl(x-R\cos\beta\bigr)=0.\end{equation} La retta per D perpendicolare a b, e quindi parallela al segmento AC ha invece equazione \begin{equation}y - y_D=m_{AC}(x-x_D)\quad\Longrightarrow\quad y={\sin\beta\over\cos\beta}(x+R)\end{equation} o anche \begin{equation}y\cos\beta-\sin\beta(x+R)=0.\end{equation} L'intersezione tra queste due rette fornisce evidentemente il punto M, punto medio del segmento DP (fig. 5.16). Le sue coordinate sono le soluzioni del sistema di I grado \begin{equation}\cases{\sin\beta\bigl(y-R\sin\beta\bigr)+\cos\beta\bigl(x-R\cos\beta\bigr)=0\cr y\cos\beta-\sin\beta(x+R)=0\cr}\end{equation} e, tramite la vista CAS di GeoGebra risultano (riga 1 di fig. 5.17),\begin{equation}\cases{x_M={R\over 2}\bigl(\cos2\beta+2\cos\beta-1\bigr)\cr\cr y_M={R\over 2}\bigl(\sin2\beta+2\sin\beta\bigr).\cr}\end{equation}
Figura 5.17. cardioide17.ggb.
Note le coordinate del punto medio, le coordinate di \(P(x,y)\) si deducono dal sistema lineare che, appunto, definisce le coordinate del punto medio di un segmento \begin{equation}\cases{{x+x_D\over 2}=x_M\cr\cr {y+y_D\over 2}=y_M\cr}\qquad\Longrightarrow\qquad \cases{{x-R\over 2}={R\over 2}\bigl(\cos2\beta+2\cos\beta-1\bigr)\cr\cr {y\over 2}={R\over 2}\bigl(\sin2\beta+2\sin\beta\bigr).\cr}\end{equation} Utilizzando ancora Geogebra (riga 2 di fig. 5.17) giungiamo alla \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x=R\bigl(2\cos\beta+\cos 2\beta\bigr)\cr y=R\bigl(2\sin\beta+\sin 2\beta\bigr)\cr}}\end{equation} del tutto identica alla coppia di equazioni aspettata \eqref{eq:1}.
Per concludere una cardioide famosa: l'insieme di Mandelbrot, attrattore della funzione a valori complessi \(f(z)=z^2+c\): ma questa è un'altra storia...
Figura 5.18. cardioide18.png.