La lemniscata di Jakob Bernoulli
- Note storiche
- Costruzione geometrica
- Equazioni rappresentative parametriche
- Equazioni polare e implicita
- Una piccola esplorazione e una definizione alternativa
- Inviluppo di circonferenze
Note storiche
Introdotta per la prima volta dal matematico svizzero Jakob Bernoulli nel 1694 come luogo dei punti per i quali il prodotto delle distanze da due punti fissi è costante, questa curva assunse notevole importanza nel corso del XVIII secolo in particolare nell'opera di Giulio Carlo Fagnano dei Toschi che ne determinò numerose proprietà in connessione con alcune classi di integrali ellittici.
Costruzione geometrica
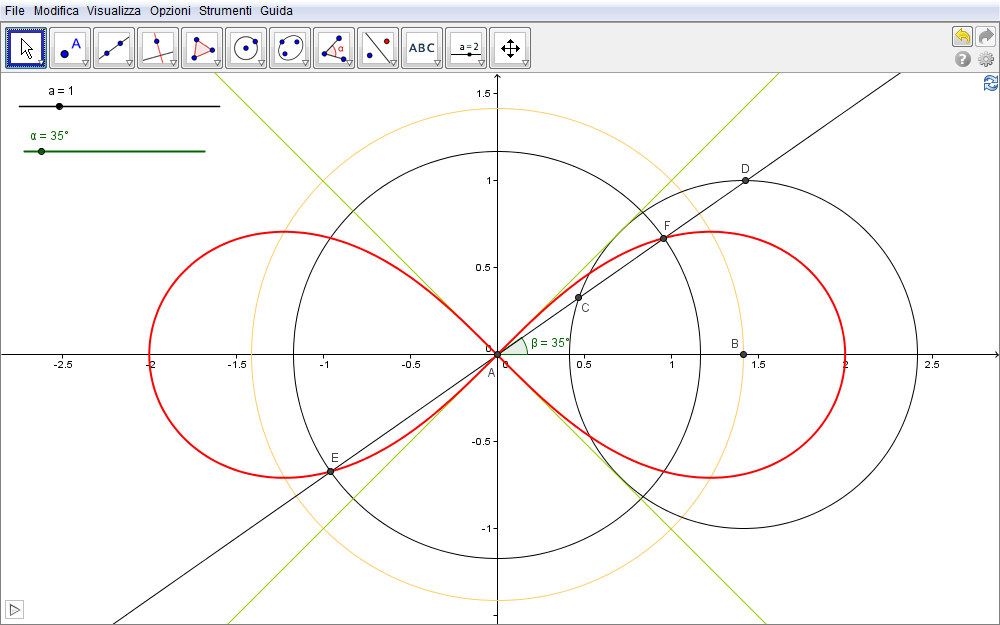
Al fine di ottenere una visualizzazione grafica della lemniscata indipendente, inizialmente, da calcoli algebrici intendiamo presentare in questa sezione la costruzione che definisce un suo punto generico P.
Figura 6.1. lemniscata01.ggb.
- Sia quindi c una circonferenza con centro nell'origine A del sistema cartesiano e quadrato del raggio pari a \(2a^2\) (con a, slider numerico positivo e che in fig. 6.1 ha valore \(a=1\)).
- Questa interseca l'asse x nel punto \(B(a\sqrt 2,0)\) e quindi,
- con centro in B, tracciamo una seconda circonferenza d avente raggio pari ad a: evidentemente questa circonferenza è tangente alle bisettrici dei quadranti del sistema (in verde in fig. 6.1) in quanto la distanza di B da queste rette è, appunto, pari al raggio \(AB \sin(45^\circ)=a\sqrt 2 \cdot (\sqrt 2/2)=a\).
- Introdotto quindi uno slider angolare \(\alpha\) angolare e
- con lo strumento Angolo di data misura
 definiamo l'angolo \(\beta=\alpha=\angle (BAB')\) e,
definiamo l'angolo \(\beta=\alpha=\angle (BAB')\) e, - tracciata la retta \(b=AB'\)
- siano C e D i suoi punti di intersezione con la circonferenza d. Manifestamente questi punti esistono quando l'angolo \(\beta\) che determina l'inclinazione della retta b assume valori nell'insieme \([0^\circ,45^\circ]\cup [135^\circ,225^\circ] \cup [315^\circ,360^\circ]\).
- Nascosto il punto \(B'\),
- con lo strumento Compasso
 tracciamo una circonferenza e di raggio CD e centro in A.
tracciamo una circonferenza e di raggio CD e centro in A. - Le intersezioni E ed F di quest'ultima con la retta b sono i punti, evidentemente simmetrici rispetto all'origine, della lemniscata.
- Lo strumento Luogo
 permette infine la visulizzazione della curva al variare dell'angolo \(\alpha\) .
permette infine la visulizzazione della curva al variare dell'angolo \(\alpha\) .
Equazioni rappresentative parametriche
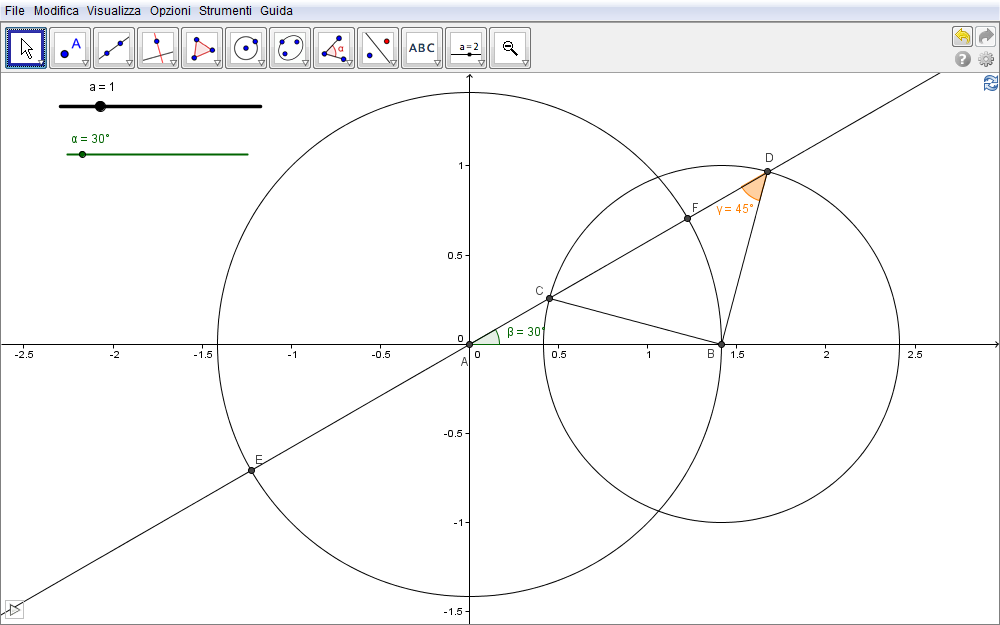
Intendiamo ora ottenere le equazioni rappresentative della lemniscata cioè le coordinate di E (o F) procedendo in modo prevalentemente analitico anziché geometrico. Scriviamo innanzitutto l'equazione della retta b per l'origine \begin{equation}b:y=x \tan\beta\label{eq:1}\end{equation} e, ricordato che \(AF=CD\), determiniamo la lunghezza del segmento \(CD\) (fig. 6.2). Osserviamo quindi che il triangolo \(\triangle(BDC)\) è isoscele con vertice in B e posto che sia \(\gamma=\angle(BDC)\), per le relazioni goniometriche sui triangoli rettangoli segue \begin{equation}CD=2(BD \cos\gamma)=2a\cos\gamma.\label{eq:2}\end{equation}
Figura 6.2. lemniscata02.ggb.
D'altra parte, applicando il teorema dei seni a \(\triangle(ABD)\) risulta \begin{equation}{AB\over \sin\gamma}={BD\over \sin\beta}\qquad\Longrightarrow\qquad {a\sqrt 2\over \sin\gamma}={a\over \sin\beta}\end{equation} in quanto, come sappiamo \(AB=a\sqrt2\) e \(BD=a\). Ricaviamo quindi \begin{equation}\sin\gamma=\sqrt 2\sin\beta\label{eq:3}\end{equation} cosicché il quadrato della \eqref{eq:2} diviene \begin{equation}CD^2=4a^2\cos^2\gamma=4a^2(1-\sin^2\gamma)=4a^2(1-2\sin^2\beta)=4a^2\cos2\beta,\label{eq:5}\end{equation} dove si sono considerate le formule di duplicazione per il coseno.
Si tratta ora di determinare le intersezioni della retta \eqref{eq:1} con la circonferenza e centrata nell'origine avente raggio pari a \(CD\) ossia \begin{equation}e: x^2+y^2=4a^2\cos2\beta.\label{eq:6}\end{equation} Il sistema di II grado \begin{equation}\cases{y=x\tan\beta\cr x^2+y^2=4a^2\cos2\beta\cr}\label{eq:7}\end{equation} fornisce facilmente i valori \begin{equation}x^2=\left(4a^2\cos2\beta\right)\cdot{1\over 1+\tan^2\beta}\qquad y^2=\left(4a^2\cos2\beta\right)\cdot {\tan^2\beta\over 1+\tan^2\beta},\label{eq:8}\end{equation} o anche per note identità goniometriche, \begin{equation}x^2=4a^2\cos2\beta\cos^2\beta\qquad y^2=4a^2\cos2\beta\sin^2\beta\end{equation} da cui le soluzioni \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x=\pm 2a\cos\beta\sqrt{\cos2\beta}\cr\cr y=\pm2a\sin\beta\sqrt{\cos2\beta}\cr}}\label{eq:10}\end{equation}
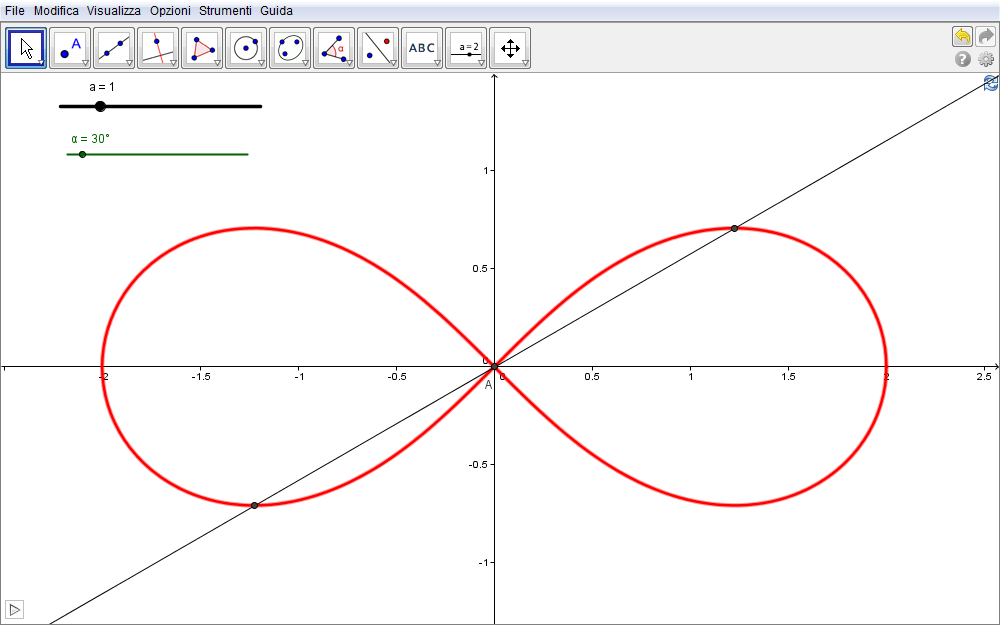
Queste sono pure le equazioni parametriche rappresentative della lemniscata per cui, inserite dalla barra di inserimento tramite il comando curva[] e nascosti tutti gli elementi accessori, GeoGebra fornisce la fig. 6.3 e permette, confrontata con la fig. 6.1, una immediata conferma grafica della correttezza delle deduzioni.
Figura 6.3. lemniscata03.ggb.
Una rappresentazione alternativa della curva si ottiene osservando che, date le limitazioni per l'angolo \(\beta\) discusse inizialmente, la \(\tan\beta\) presente nelle \eqref{eq:8} assume valori nell'intervallo \(\tan\beta\in[-1,1]\). Se quindi poniamo \begin{equation}\tan\beta=\sin t\qquad\hbox{con}\qquad t\in[0,2\pi],\label{eq:11}\end{equation} dove \(t\) rappresenta un nuovo parametro, e ricordiamo l'identità \begin{equation}\cos2\beta={1-\tan^2\beta\over 1+\tan^2\beta}\label{eq:12}\end{equation} le \eqref{eq:8} si possono riscrivere \begin{equation}x^2=4a^2\biggl({1-\tan^2\beta\over 1+\tan^2\beta}\biggr)\cdot{1\over 1+\tan^2\beta}\qquad y^2=4a^2\biggl({1-\tan^2\beta\over 1+\tan^2\beta}\biggr)\cdot{\tan^2\beta\over 1+\tan^2\beta}\end{equation} e quindi con il cambio di parametro \eqref{eq:11} si riducono a \begin{equation}x^2=4a^2\cdot{1-\sin^2t\over (1+\sin^2t)^2},\qquad y^2=4a^2\cdot{1-\sin^2t\over (1+\sin^2t)^2}\cdot \sin^2t\end{equation} dalle quali discendono \begin{equation}x^2={4a^2\cos^2t\over (1+\sin^2t)^2},\qquad y^2={4a^2\cos^2t\over (1+\sin^2t)^2}\cdot \sin^2t\end{equation} e quindi, \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x={2a\cos t\over 1+\sin^2t}\cr\cr y={2a\sin t\cos t\over 1+\sin^2t}.\cr}}\label{eq:16}\end{equation} Queste equazioni evitano quindi l'uso della radice quadrata e sono considerate le equazioni canoniche per la lemniscata assieme alle \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x={2a\sin t\over 1+\cos^2t}\cr\cr y={2a\sin t\cos t\over 1+\cos^2t},\cr}}\label{eq:17}\end{equation} ottenute con la sostituzione \(\tan\beta=\cos t\), alternativa alla \eqref{eq:11}.
Infine, se esprimiamo le funzioni goniometriche coinvolte in \eqref{eq:17} con le identità \[\sin t= {2 w\over 1+w^2},\qquad \cos t={1-w^2\over 1+w^2},\qquad\hbox{dove si è posto}\quad w=\tan{t\over 2},\] allora giungiamo ad una rappresentazione razionale della curva espressa dalle \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x={2a\, w(1+w^2)\over 1+w^4}\cr \cr y={2a\,w(1-w^2)\over 1+w^4}\cr}\qquad w\in\,]-\infty,+\infty[.}\end{equation} Nota: il simbolo matematico di infinito, \(\infty\), è una lemniscata di Bernoulli!
Equazioni polare e implicita
Se sostituiamo al sistema cartesiano utilizzato finora, un sistema polare di coordinate \((\rho,\beta)\) con polo nell'origine A, asse polare coincidente con il semiasse positivo delle x e anomalia \(\beta\) (fig. 1), l'equazione che descrive la lemniscata ne discende immediata dall'equazione della circonferenza e determinata in \eqref{eq:6} \[e:x^2+y^2=4a^2\cos2\beta.\] Difatti basta porre \(\rho^2=x^2+y^2\) per ottenere l'equazione polare \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\rho^2=4a^2\cos2\beta.}\end{equation}
L'equazione rappresentativa implicita si ottiene ancora dalla \eqref{eq:6} riscrivendo il II membro in termini della \(\tan\beta\) ossia utilizzando l'identità \eqref{eq:12} \[e:x^2+y^2=4a^2\cdot {1-\tan^2\beta\over 1+\tan^2\beta}.\] Poiché dalla \eqref{eq:1} è pure \[\tan^2\beta={y^2\over x^2},\] sostituita nella precedente otteniamo \[x^2+y^2=4a^2\cdot {1-(y^2/x^2)\over 1+(y^2/x^2)}\] dalla quale \[x^2+y^2=4a^2\cdot {x^2-y^2\over x^2+y^2}\] e quindi \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\bigl(x^2+y^2\bigr)^2=4a^2\bigl(x^2-y^2\bigr).}\label{eq:20}\end{equation} L'equazione cartesiana implicita della lemniscata di Bernoulli è di conseguenza un'equazione razionale in due variabili di quarto grado.
Una piccola esplorazione e una definizione alternativa
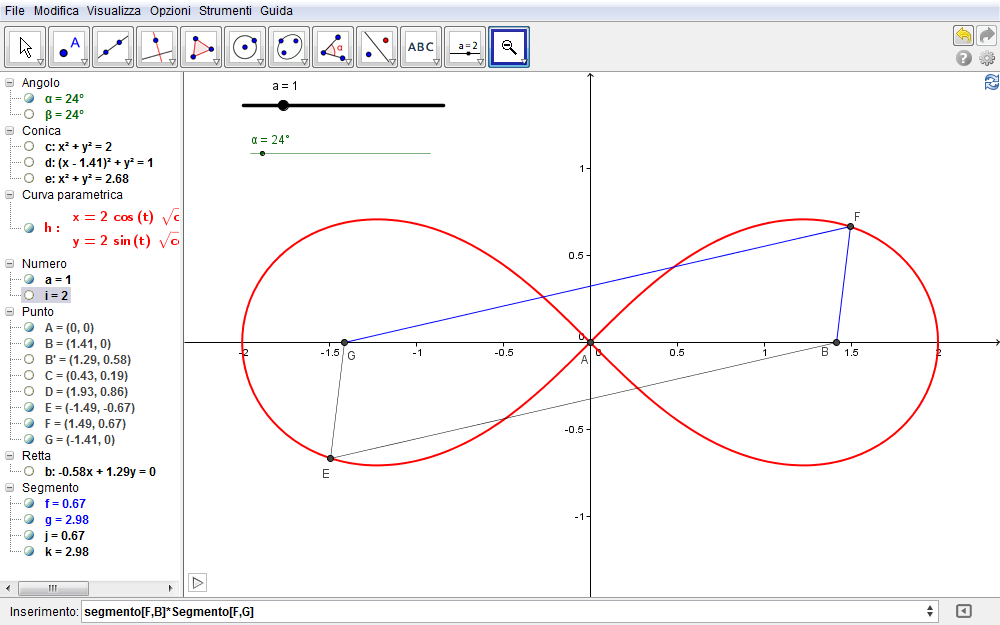
Riprendiamo le figg. 6.1 e 6.3 evidenziando il centro B del cerchio d (di raggio a) e
Figura 6.4. lemniscata04.ggb.
- costruiamo il suo simmetrico G rispetto all'origine A.
- Se ora tracciamo i due segmenti \(FB\) e \(FG\) e, nella barra di inserimento,
- immettiamo il prodotto delle lunghezze, segmento[F,B]*segmento[F,G], a cui GeoGebra associa il numero i (fig. 6.4)
- e quindi avviamo l'animazione,
si nota facilmente come tale valore (\(i=2\) in fig. 6.4) rimanga costante al variare del punto: il prodotto quindi delle distanze di un punto della lemniscata da due opportuni punti fissi sembra essere indipendente dal punto stesso. Converrà quindi studiare formalmente tale osservazione.
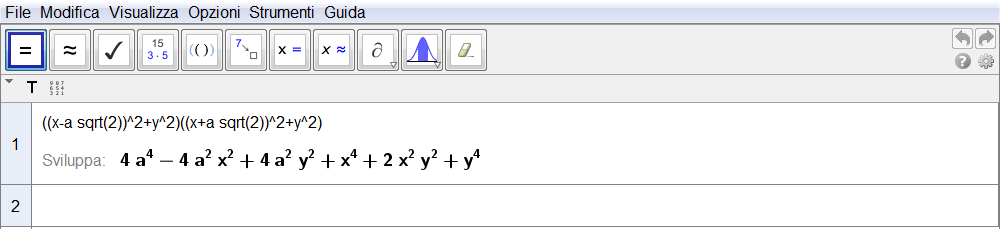
Per come è stato definito, le coordinate di B sono \(B(a\sqrt 2,0)\) e, poiché G è il simmetrico rispetto all'origine, è pure \(G(-a\sqrt 2,0)\). Il punto generico F della lemniscata ha invece coordinate \(F(x,y)\) e, per quanto dedotto precedentemente soddisfa, per esempio, l'equazione \eqref{eq:20}. Con lo stesso metodo standard che conduce alle equazioni canoniche dell'ellisse e dell'iperbole, scritte le distanze \begin{equation}FB=\sqrt{\bigl(x-a\sqrt 2\bigr)^2+y^2},\qquad FG=\sqrt{\bigl(x+a\sqrt 2\bigr)^2+y^2},\label{eq:21}\end{equation} il loro prodotto risulta \begin{equation}FB\cdot FG=\sqrt{\bigl(x-a\sqrt 2\bigr)^2+y^2}\cdot \sqrt{\bigl(x+a\sqrt 2\bigr)^2+y^2}\end{equation} o anche \begin{equation}FB\cdot FG=\sqrt{\bigl[\bigl(x-a\sqrt 2\bigr)^2+y^2\bigr]\cdot \bigl[\bigl(x+a\sqrt 2\bigr)^2+y^2\bigr]}\end{equation} Demandando alla vista CAS di GeoGebra i calcoli algebrici sotto radice (fig. 6.5) otteniamo \begin{equation}FB\cdot FG=\sqrt{4a^4-4a^2x^2+4a^2y^2+x^4+2x^2y^2+y^4}.\end{equation}
Figura 6.5. lemniscata05.ggb.
Osservando gli ultimi tre termini del radicando e i fattori comuni, questo si può riscrivere anche come \begin{equation}FB\cdot FG=\sqrt{4a^4-4a^2(x^2-y^2)+(x^2+y^2)^2}\end{equation} per cui inserendo il risultato \eqref{eq:20} \begin{equation}FB\cdot FG=\sqrt{4a^4-4a^2(x^2-y^2)+4a^2(x^2-y^2)}\end{equation} si riduce a \begin{equation}FB\cdot FG=\sqrt{4a^4}=2a^2,\end{equation} risultato che conferma quanto ottenuto numericamente inizialmente. Difatti posto \(a=1\) si ritrova il valore 2 del prodotto.
Possiamo ora fornire una sintetica definizione della lemniscata di Bernoulli: questa si potrà identificare come il
luogo dei punti del piano tali che il prodotto delle distanze da due punti fissi è pari ad una costante.
Se, in analogia all'ellisse e all'iperbole, individuiamo i punti fissi (che chiameremo fuochi della lemniscata) con le coordinate \(F_1(f,0)\) e \(F_2(-f,0)\) dove \(f=a\sqrt 2\), e con \(P(x,y)\) un punto generico, la condizione che individua la curva assume la forma sintetica \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{PF_1\cdot PF_2=f^2}\end{equation}
Inviluppo di circonferenze
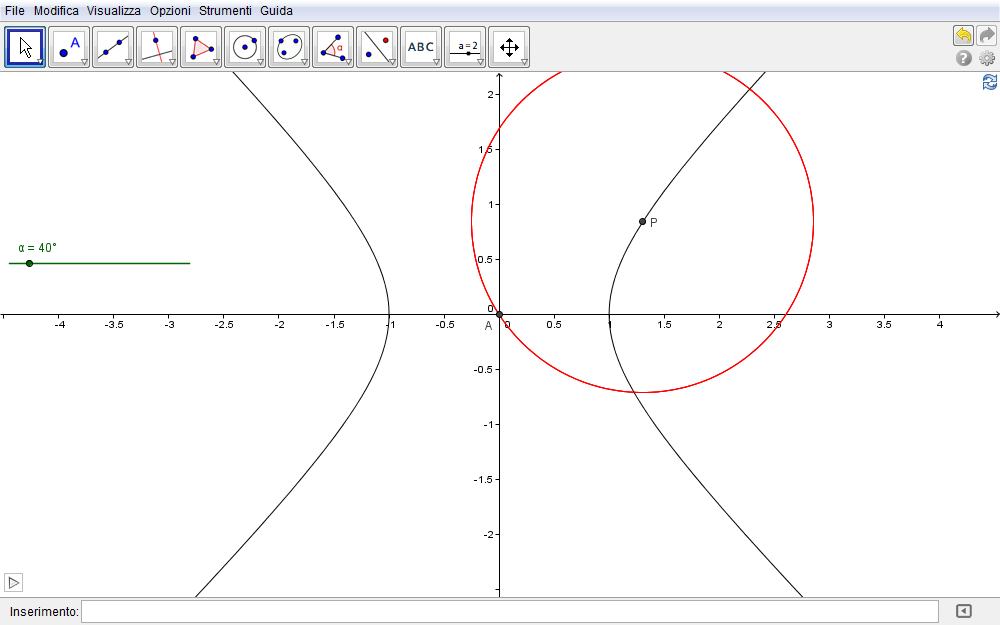
Intendiamo qui ottenere la lemniscata come inviluppo di una famiglia di circonferenze passanti per l'origine del sistema cartesiano e il cui centro sia un punto di una iperbole equilatera. La visualizzazione con GeoGebra è immediata non appena (fig. 6.6) si tenga presente la rappresentazione parametrica di un'iperbole equilatera. Difatti,
Figura 6.6. lemniscata06.ggb.
- immessa nella barra di inserimento l'equazione cartesiana canonica dell'iperbole equilatera \(x^2-y^2=a^2\) con \(a=1\),
- definiamo uno slider angolare \(\alpha\) e quindi,
- costruito il punto A coincidente con l'origine,
- definiamo il punto sull'iperbole tramite la sua rappresentazione parametrica. A tal fine basta immettere nella barra di inserimento \(P=(a\sec(\alpha),a\tan(\alpha))\).
- Infine tracciare la circonferenza di centro P e raggio PA e,
- attivata la traccia di quest'ultima,
- avviare l'animazione dello slider per ottenere la fig. 6.7.
Figura 6.7. lemniscata07.ggb.
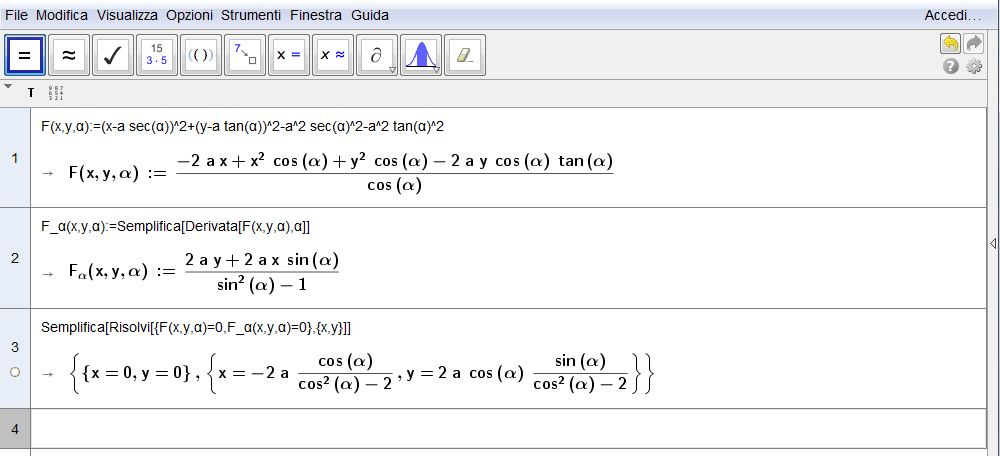
Sappiamo che, per ottenere la rappresentazione della curva inviluppo, è necessario costruire innanzitutto la famiglia, in questo caso di circonferenze, che la origina. Poichè il centro è noto, \(P(a\sec\alpha,a\tan\alpha)\), determiniamo il quadrato del raggio \[PA^2=x_P^2+y_P^2=a^2\sec^2\alpha+a^2\tan^2\alpha.\] Ne segue che la famiglia di circonferenze è espressa dall'equazione \[(x-x_P)^2+(y-y_P)^2=PA^2\] e più esplicitamente dall'equazione parametrica \begin{equation}(x-a\sec\alpha)^2+(y-a\tan\alpha)^2=a^2\sec^2\alpha+a^2\tan^2\alpha.\label{eq:29}\end{equation} Possiamo di conseguenza definire la funzione \begin{equation}F(x,y,\alpha)=(x-a\sec\alpha)^2+(y-a\tan\alpha)^2-a^2\sec^2\alpha-a^2\tan^2\alpha\end{equation} e quindi calcolare la sua derivata parziale rispetto ad \(\alpha\), \(F_\alpha(x,y,\alpha)\) utilizzando allo scopo GeoGebra (riga 2, fig. 6.8) \begin{equation}F_\alpha(x,y,\alpha)={2a y+2a x\sin\alpha\over \sin^2\alpha-1}.\end{equation}
Figura 6.8. lemniscata08.ggb.
Il sistema (di II grado) \begin{equation}\cases{F(x,y,\alpha)=0\cr F_\alpha(x,y,\alpha)=0\cr}\end{equation} fornisce quindi la soluzione (riga 3, fig. 6.8)\begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x={2a\cos\alpha\over 2-\cos^2\alpha}\cr\cr y={2a\sin\alpha\cos\alpha\over \cos^2\alpha-2}\cr}}\end{equation} che coincide con la coppia \eqref{eq:16} non appena si consideri al denominatore che \(2-\cos^2\alpha=1+\sin^2\alpha\). Aggiunte queste equazioni tramite il comando curva[], la fig. 6.9 conferma visivamente come la lemniscata sia l'inviluppo di una opportuna famiglia di circonferenze.
Figura 6.9. lemniscata09.ggb.
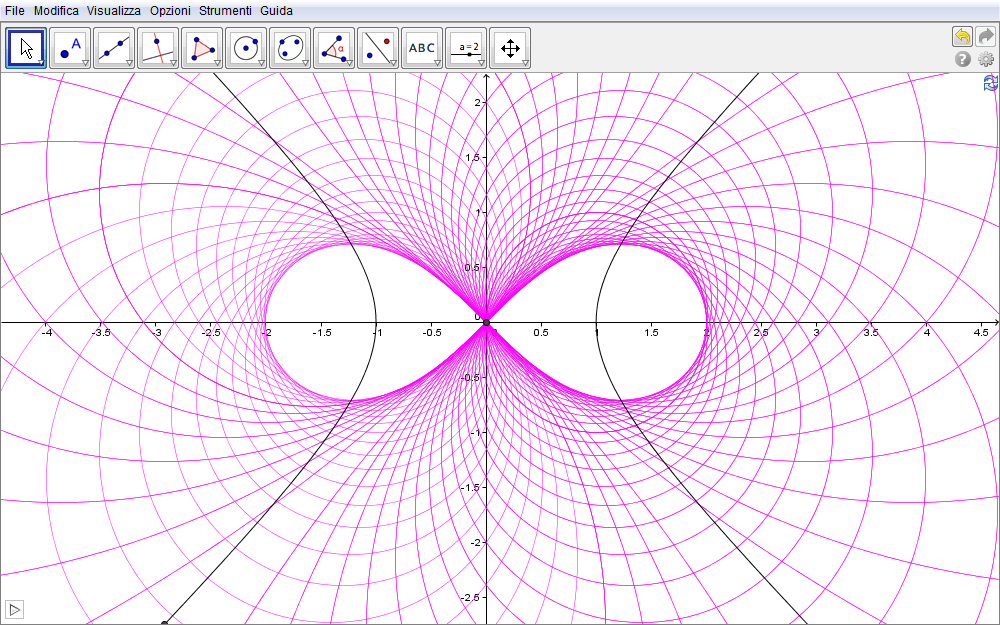
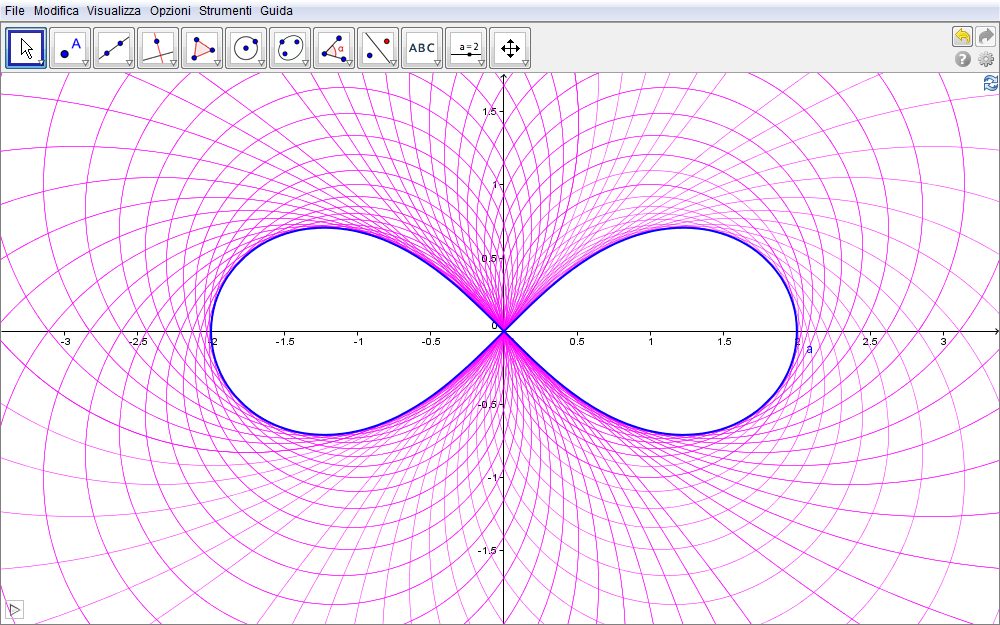
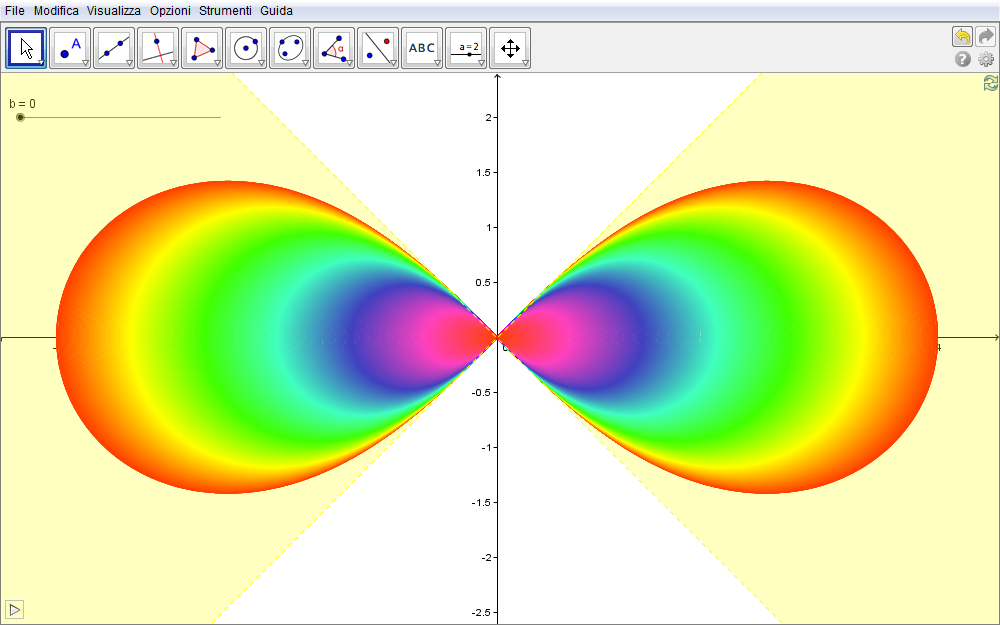
Infine, la figura seguente rappresenta in colore una densa famiglia di lemniscate di Bernoulli, tutte comprese nella regione, in colore, espressa dalla disequazione \(x^2\geq y^2\).
Figura 6.10. lemniscata10.ggb.