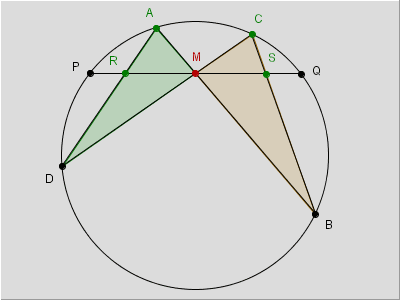
figura 1
In questa pagina presentiamo un teorema che, per la figura cui dà origine, viene spesso individuato come il teorema della farfalla. Di questo teorema, pubblicato per la prima volta in forma di problema nel 1815 in una rivista di matematica, si possono trovare numerose dimostrazioni: noi ne proporremo quattro, le prime tre di carattere sintetico, l'ultima di carattere algebrico.
Tra i teoremi della geometria elementare che coinvolgono corde e cerchi il teorema della "farfalla" (Butterfly theorem nei paesi anglosassoni) non sempre appare conosciuto forse perché le sue dimostrazioni appaiono abbastanza articolate pur non coinvolgendo nozioni particolarmente avanzate.
Di questo teorema proporremo diverse prove, ciascuna con le proprie peculiarietà.
I dimostrazione. Da R e S tracciamo le perpendicolari alle corde AB e CD e siano R1 e, rispettivamente, R2 le loro intersezioni (fig. 2). Analogamente facciamo da S cosicché S1 è l'intersezione della perpendicolare per S ad AB e S2 l'analogo punto che si ottiene dalla corda CD.
figura 2
È immediato notare le seguenti similitudini tra triangoli rettangoli
e dove le ultime due derivano dalla congruenza rispettivamente degli angoli alla circonferenza ![]() DAB =
DAB = ![]() DCB e
DCB e ![]() ADC =
ADC = ![]() ABC.
ABC.
In corrispondenza possiamo impostare le quattro proporzioni
| MR MS |
= | RR1 SS1 |
(1) | |
| MR MS |
= | RR2 SS2 |
(2) | |
| RR1 SS2 |
= | AR CS |
(3) | |
| RR2 SS1 |
= | RD SB |
(4) |
Moltiplichiamo i primi membri di (1) e (2)
| MR MS |
· | MR MS |
= | RR1 SS1 |
· | RR2 SS2 |
e quindi commutiamo i fattori a denominatore del secondo membro
| MR MS |
· | MR MS |
= | RR1 SS2 |
· | RR2 SS1 |
Possiamo ora applicare la (3) e (4) ottenendo
| MR MS |
· | MR MS |
= | AR CS |
· | RD SB |
Ricordando che il teorema delle secanti afferma che il punto comune di due corde secanti divide ciascuna delle corde in due parti che sono rispettivamente i medi e gli estremi di una proporzione ed applicandolo alle coppie di corde AD, PQ e CB PQ, deduciamo
| AR x RD | = | PR x RQ | CS x SB | = | PS x SQ |
per cui risulta
| MR MS |
· | MR MS |
= | PR · RQ PS · SQ |
(5) |
Poiché è immediato notare la validità delle relazioni seguenti (fig. 2)
| PR | = | PM - MR | ||
| RQ | = | MR + MQ | = | PM + MR |
| PS | = | PM + MS | ||
| SQ | = | MQ - MS | = | PM - MS |
dove si è tenuto conto del fatto che M è il punto medio di PQ, la (5) si riscrive come
| MR2 MS2 |
= | (PM - MR)(PM + MR) (PM + MS)(PM - MS) |
e in definitiva
| MR2 MS2 |
= | PM2 - MR2 PM2 - MS2 |
Moltiplicando entrambi i membri per (PM2 - MS2) / MR2 si ottiene
| PM2 - MS2 MS2 |
= | PM2 - MR2 MR2 |
cioè
| PM2 MS2 |
- | 1 | = | PM2 MR2 |
- | 1 |
da cui
| PM2 MS2 |
= | PM2 MR2 |
Avendo i due rapporti il medesimo numeratore, si deduce che MR2 = MS2 cioè MR = MS: il punto M appare, in conclusione, il punto medio di RS e ciò è la tesi che si voleva dimostrare.
Dimostriamo un facile teorema che riguarda i quadrilateri inscritti in un cerchio in quanto ci verrà utile in una seconda dimostrazione del teorema appena esposto. Intendiamo quindi dimostrare che
Si tratta di dimostrare che, se ![]() ACB =
ACB = ![]() ADB allora ABCD è inscritto in un cerchio (fig. 3).
ADB allora ABCD è inscritto in un cerchio (fig. 3).
Procediamo per assurdo negando la tesi per cui uno dei quattro vertici, per esempio, D non appartenga alla circonferenza. In tale ipotesi D potrà essere esterno o interno ad essa. Supponiamo inizialmente che sia esterno (fig. 4): in tal caso la diagonale BD interseca in un punto D1 la circonferenza passante per i rimanenti tre punti cosicché a seguito del teorema sugli angoli alla circonferenza è ![]() ACB =
ACB = ![]() AD1B. D'altra parte quest'ultimo angolo risulta angolo esterno a
AD1B. D'altra parte quest'ultimo angolo risulta angolo esterno a ![]() AD1D per cui
AD1D per cui
e quindi ![]() AD1B >
AD1B > ![]() ADB. Per quanto sopra questa diseguaglianza si può riscrivere come
ADB. Per quanto sopra questa diseguaglianza si può riscrivere come ![]() ACB >
ACB > ![]() ADB manifestamente contro l'ipotesi che sia
ADB manifestamente contro l'ipotesi che sia ![]() ACB =
ACB = ![]() ADB.
ADB.
Nel caso D sia interno alla circonferenza passante per A, B, C (si sposti D in figura 4 internamente alla circonferenza) è ancora possibile definire il punto D1 quale intersezione del prolungamento di BD con la circonferenza e quindi individuare la congruenza ![]() ACB =
ACB = ![]() AD1B. Questa volta risulta
AD1B. Questa volta risulta ![]() ADB esterno a
ADB esterno a ![]() ADD1 per cui
ADD1 per cui ![]() ADB >
ADB > ![]() AD1B ossia
AD1B ossia ![]() ADB >
ADB > ![]() ACB, contro l'ipotesi. In definitiva D deve appartenere alla circonferenza per A, B, C ossia questi quattro punti sono conciclici.
ACB, contro l'ipotesi. In definitiva D deve appartenere alla circonferenza per A, B, C ossia questi quattro punti sono conciclici.
Siamo ora in grado di proporre una seconda dimostrazione del teorema della farfalla deduzione che, per poter essere generale, converrà sviluppare in due momenti diversi.
I parte. In riferimento alla figura 5, tracciamo la corda DH![]() PQ, la retta per M, perpendicolare a DH in N e i segmenti MH, SH e BH.
PQ, la retta per M, perpendicolare a DH in N e i segmenti MH, SH e BH.
figura 5
Dato il parallelismo tra PQ e DH e la perpendicolarità di MN con DH, MN risulta pure perpendicolare a PQ cosicché passando, per costruzione, per il suo punto medio, ne costituisce l'asse. Il centro del cerchio dovrà appartenere quindi a tale retta e conseguentemente questa risulta pure l'asse della corda DH in quanto una retta passante per il centro di un cerchio e perpendicolare ad una corda costituisce l'asse di quest'ultimo segmento.
Ne segue che
| MD = MH | e |
e quindi pure ![]() DMN =
DMN = ![]() NMH: un'analoga congruenza vale perciò per i rispettivi complementari
NMH: un'analoga congruenza vale perciò per i rispettivi complementari ![]() RMD =
RMD = ![]() SMH (oppure
SMH (oppure ![]() PMD =
PMD = ![]() QMH).
QMH).
Sia ora O il centro del cerchio e tracciamo i raggi PO, DO, CO, QO e OH (fig. 6). Questi permettono di definire gli angoli al centro ![]() DOP e
DOP e ![]() COQ collegabili all'angolo
COQ collegabili all'angolo ![]() PMD formato dalle corde PQ e CD. La relazione che lega l'angolo formato da due corde con gli angoli al centro intercettati dalle medesime corde è fornita dal teorema seguente
PMD formato dalle corde PQ e CD. La relazione che lega l'angolo formato da due corde con gli angoli al centro intercettati dalle medesime corde è fornita dal teorema seguente
In base a ciò
| = | 1 2 |
( |
e quindi, essendo ![]() DOP =
DOP = ![]() QOH in quanto angoli al centro che insistono su archi congruenti (si vedano i teoremi sulle corde parallele e sulla congruenza di angoli al centro),
QOH in quanto angoli al centro che insistono su archi congruenti (si vedano i teoremi sulle corde parallele e sulla congruenza di angoli al centro),
| = | 1 2 |
( |
|||||
| = | 1 2 |
( |
= | (6) |
dove, nell'ultimo passaggio si è sfruttata la conguenza già vista. D'altra parte l'angolo alla circonferenza ![]() CBH è la metà di quello al centro
CBH è la metà di quello al centro ![]() COH (in fig. 7 quest'ultimo angolo è quello concavo)
COH (in fig. 7 quest'ultimo angolo è quello concavo)
| = | = | 1 2 |
(7) |
per cui sommando la (6) e la (7) si ottiene
| + | = | 1 2 |
( |
e notando che ![]() QOH +
QOH + ![]() COQ +
COQ + ![]() COH = 360°, si deduce
COH = 360°, si deduce
| + | = | 180° |
che mostra come i due angoli ![]() SMH e
SMH e ![]() SBH siano supplementari e che quindi il quadrilatero SMHB sia ciclico. Tracciata la circonferenza passante per questi quattro punti (fig. 8) è immediato dedurre la congruenza tra gli angoli alla circonferenza
SBH siano supplementari e che quindi il quadrilatero SMHB sia ciclico. Tracciata la circonferenza passante per questi quattro punti (fig. 8) è immediato dedurre la congruenza tra gli angoli alla circonferenza ![]() MHS =
MHS = ![]() MBS ed essendo, per lo stesso motivo sulla circonferenza originaria,
MBS ed essendo, per lo stesso motivo sulla circonferenza originaria, ![]() ABC =
ABC = ![]() ADC cioè
ADC cioè ![]() MBS =
MBS = ![]() MDR, la transitività della congruenza implica
MDR, la transitività della congruenza implica ![]() MHS =
MHS = ![]() MDR.
MDR.
Ne segue che i triangoli ![]() RDM e
RDM e ![]() MHS avendo ordinatamente congruenti due angoli,
MHS avendo ordinatamente congruenti due angoli, ![]() RMD =
RMD = ![]() SMH,
SMH, ![]() MDR =
MDR = ![]() MHS e il lato compreso MD = MH, sono pure essi congruenti: in particolare risulta MR = MS come volevasi dimostrare.
MHS e il lato compreso MD = MH, sono pure essi congruenti: in particolare risulta MR = MS come volevasi dimostrare.
II parte. Se spostiamo il punto D della figura 8 in modo che H passi dall'arco DB all'arco BQ (fig. 9) osserviamo che i punti M, B, H e S rimangono ancora conciclici ma non risulta più valida la relazione ![]() SMH +
SMH + ![]() SBH = 180°. Dobbiamo quindi cercare un modo alternativo per dimostrare ancora la ciclicità di questi quattro punti.
SBH = 180°. Dobbiamo quindi cercare un modo alternativo per dimostrare ancora la ciclicità di questi quattro punti.
A tal fine osserviamo che ![]() SMH =
SMH = ![]() MHD in quanto alterni interni di rette parallele mentre già conosciamo che
MHD in quanto alterni interni di rette parallele mentre già conosciamo che ![]() MHD =
MHD = ![]() MDH dato che
MDH dato che ![]() MDH è isoscele. Poiché
MDH è isoscele. Poiché ![]() MDH si può vedere come l'angolo alla circonferenza
MDH si può vedere come l'angolo alla circonferenza ![]() CDH discende immediatamente che
CDH discende immediatamente che ![]() CDH =
CDH = ![]() CBH =
CBH = ![]() SBH. Abbiamo pertanto che
SBH. Abbiamo pertanto che ![]() SMH =
SMH = ![]() SBH per cui possiamo applicare il teorema dimostrato nella sezione precedente che afferma, anche in questo caso, la ciclicità dei punti M, B, H, S. La generalità della dimostrazione è in tal modo assicurata.
SBH per cui possiamo applicare il teorema dimostrato nella sezione precedente che afferma, anche in questo caso, la ciclicità dei punti M, B, H, S. La generalità della dimostrazione è in tal modo assicurata.
Tracciato il segmento perpendicolare per il centro O al punto medio M di PQ, l'ulteriore dimostrazione che presentiamo si basa sull'osservazione che si avrà MR = MS se e solo se riusciremo a dimostrare che i due triangoli rettangoli ![]() MRO e
MRO e ![]() MSO sono congruenti il che equivale a dimostrare che sia
MSO sono congruenti il che equivale a dimostrare che sia ![]() ROM =
ROM = ![]() SOM dato che i suddetti triangoli possiedono già MO come lato in comune (fig. 10).
SOM dato che i suddetti triangoli possiedono già MO come lato in comune (fig. 10).
Sulla figura precedente aggiungiamo i segmenti OH e OK perpendicolari rispettivamente alle corde AD e CB (fig. 11).
figura 11
Dato che ![]() DAB =
DAB = ![]() DCB e
DCB e ![]() ADC =
ADC = ![]() ABC (coppie di angoli che insistono sullo stesso arco) segue la similitudine dei triangoli
ABC (coppie di angoli che insistono sullo stesso arco) segue la similitudine dei triangoli ![]() ADM
ADM![]()
![]() CBM per cui si giustifica l'uguaglianza tra i rapporti
CBM per cui si giustifica l'uguaglianza tra i rapporti
| AD AM |
= | CB CM |
Poiché H e K sono i punti medi di AD e CB in quanto ![]() DOA e
DOA e ![]() COB sono isosceli, possiamo sostituire nella proporzione precedente le relazioni AD = 2 AH e CB = 2 CK ottenendo
COB sono isosceli, possiamo sostituire nella proporzione precedente le relazioni AD = 2 AH e CB = 2 CK ottenendo
| 2AH AM |
= | 2CK CM |
da cui | AH AM |
= | CK CM |
Consideriamo ora ![]() AHM e
AHM e ![]() CKM. Per quanto appena ottenuto questi triangoli hanno due lati corrispondenti in proporzione e gli angoli compresi congruenti (
CKM. Per quanto appena ottenuto questi triangoli hanno due lati corrispondenti in proporzione e gli angoli compresi congruenti (![]() HAM =
HAM = ![]() KCM). Pertanto per il secondo criterio di similitudine è
KCM). Pertanto per il secondo criterio di similitudine è ![]() AHM
AHM![]()
![]() CKM e, in particolare, discende che
CKM e, in particolare, discende che
| = | che può essere riscritta come | = | (8) |
Osserviamo ora i quadrilateri RHOM e SKOM (fig. 12). Avendo ciascuno una coppia di angoli opposti retti (e quindi supplementari), in particolare ![]() RHO e
RHO e ![]() OMR per RHOM,
OMR per RHOM, ![]() SKO e
SKO e ![]() OMS per SKOM (fig. 11), risultano entrambi inscrivibili in una circonferenza per cui discendono le congruenze
OMS per SKOM (fig. 11), risultano entrambi inscrivibili in una circonferenza per cui discendono le congruenze
| = | = |
figura 12
Per la (8) ciò significa che ![]() ROM =
ROM = ![]() SOM da cui, come previsto, deriva la congruenza dei triangoli rettangoli
SOM da cui, come previsto, deriva la congruenza dei triangoli rettangoli ![]() MRO
MRO![]()
![]() MSO e quindi dei lati MR e MS.
MSO e quindi dei lati MR e MS.
L'ultima dimostrazione che presentiamo vuole, diversamente dalle precedenti, seguire un approccio algebrico basato sul teorema trigonometrico dei seni. Per rendere le espressioni algebriche che costruiremo più snelle converrà introdurre una simbologia adeguata ponendo, in riferimento alla figura 13:
| RM | = | x | = | α | = | γ | ||||
| PM | = | a | = | β | = | δ |
figura 13
Come nella prima dimostrazione partiamo dalla applicazione del teorema delle secanti per cui, considerando queste ultime come i segmenti AD e PQ abbiamo
| AR | · | RD | = | PR | · | RQ | cioè | AR | · | RD | = | (a - x)·(a + x) | = | a2 - x2 | (9) |
Esprimiamo ora tramite il teorema dei seni le lunghezze dei segmenti a primo membro di questa relazione. Allora in ![]() ARM si ha
ARM si ha
| AR sen α |
= | RM sen γ |
e quindi | AR | = | x sen α sen γ |
Ragionando allo stesso modo in ![]() RDM deduciamo
RDM deduciamo
| RD sen β |
= | RM sen δ |
e quindi | RD | = | x sen β sen δ |
e poiché comunque vale la relazione
| δ + α + β + γ | = | 180° |
in quanto somma degli angoli interni di un triangolo, l'ultimo rapporto si riscrive come
| RD | = | x sen β sen (180° - α - β - γ) |
da cui | RD | = | x sen β sen (α + β + γ) |
Inserendo questi risultati nel primo membro della (9) abbiamo
| x sen α sen γ |
· | x sen β sen (α + β + γ) |
= | a2 - x2 |
dalla quale, moltiplicando per il denominatore,
| x2 sen α sen β | = | (a2 - x2) sen γ sen (α + β + γ). |
Esplicitando x2
| x2 [sen α sen β + sen γ sen (α + β + γ)] | = | a2 sen γ sen (α + β + γ) |
si ottiene in definitiva
| x2 | = | a2 sen γ sen (α + β + γ) sen α sen β + sen γ sen (α + β + γ) |
(10) |
Dovremmo ora procedere allo stesso modo per determinare il segmento incognito MS a partire dalla proprietà
| CS | · | SB | = | PS | · | SQ. |
Notiamo comunque che l'unica differenza tra il procedimento seguito e quest'altro consiste nello scambio degli angoli α e β interni a ![]() SMB e
SMB e ![]() CMS. L'espressione per MS cui si giunge è pertanto del tutto analoga a quella appena ottenuta tranne che per lo scambio di questi due angoli. Ma, dato che α e β appaiono nella (10) coinvolti in una somma (commutativa) o nel prodotto dei rispettivi seni (pure commutativo), la stessa (10) risulta simmetrica rispetto a tale scambio per cui entrambe devono esprimere la medesima quantità: possiamo quindi concludere in tutta generalità che MR = MS.
CMS. L'espressione per MS cui si giunge è pertanto del tutto analoga a quella appena ottenuta tranne che per lo scambio di questi due angoli. Ma, dato che α e β appaiono nella (10) coinvolti in una somma (commutativa) o nel prodotto dei rispettivi seni (pure commutativo), la stessa (10) risulta simmetrica rispetto a tale scambio per cui entrambe devono esprimere la medesima quantità: possiamo quindi concludere in tutta generalità che MR = MS.
Tutte le dimostrazioni presentate finora hanno considerato i punti R ed S come appartenenti strettamente alla corda PQ e intersezioni con questa dei segmenti AD e BC. Il problema che proponiamo vuole invece generalizzare l'affermazione del teorema pure a punti appartenenti ai prolungamenti di PQ.
Problema 10.1. Se per il punto medio M di una corda PQ di un cerchio si conducono due altre corde AB e CD e le rette BD e AC intersecano la retta PQ rispettivamente in R e S, allora M risulta il punto medio di RS.
Dimostrazione
|
|
||||||||||