La versiera di Gaetana Agnesi
- Notizie storiche
- Costruzione e definizione
- Equazioni parametriche rappresentative
- Equazione cartesiana e funzione
Notizie storiche
Maria Gaetana Agnesi (1718-1799) è una matematica italiana nota per aver pubblicato nel 1748 un trattato di analisi dal titolo "Instituzioni analitiche ad uso della gioventù italiana". Ricevette grandi onori professionali e, secondo G. Fichera, "l'Agnesi è forse l'unico esempio fra le donne matematiche che non abbia incontrato difficoltà per poter portare avanti una attività accademica".
Gaetana Agnesi ha legato il suo nome alla versiera (presente nel suo trattato del 1748), una curva che peraltro non fu scoperta da lei, ma da Guido Grandi. Grandi l'aveva chiamata curva con seno verso (sinus versus) cioè inverso del seno ma pure contrario, nemico. Di qui, versiera, "avversaria", nome solitamente attribuito alle streghe. Infatti in inglese la curva è nota come witch of Agnesi (strega di Agnesi).
Costruzione e definizione
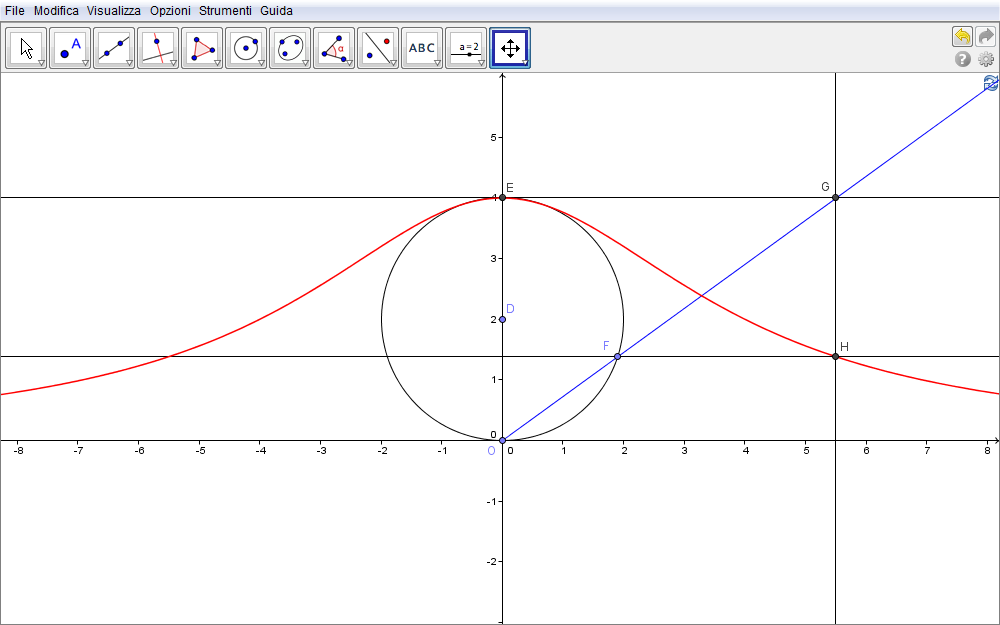
Con riferimento alla figura seguente riportiamo i passi della costruzione geometrica che definiscono la versiera.
Figura 1.1. versiera01.ggb.
- Costruita la retta AB coincidente con l'asse x di un sistema cartesiano xOy,
- sia \(O(0,0)\) l'origine.
- Tracciato una retta per O perpendicolare alla retta \(AB\)) (asse y),
- sia D un punto su tale asse (in figura \(D(0,2)\)),
- c la circonferenza per O di centro D e
- E la sua intersezione con l'asse y.
- Tracciare ora la retta d per E parallela all'asse x e
- definire un punto F appartenente alla circonferenza c.
- È quindi possibile introdurre la semiretta OF che
- incontra la retta d in G.
- Costruita la retta f per G e perpendicolare a d e
- la retta g per F e parallela all'asse x,
- queste si intersecano nel punto H.
- È sufficiente chiedere la visualizzazione del luogo dei punti H al variare di F sulla circonferenza per ottenere la versiera. Trascinando F nella figura 1.1 si constata come H appartenga al luogo evidenziato in rosso.
In termini analitici, la versiera è quindi il luogo dei punti H aventi l'ascissa di G e l'ordinata di F al descrivere di F la circonferenza.
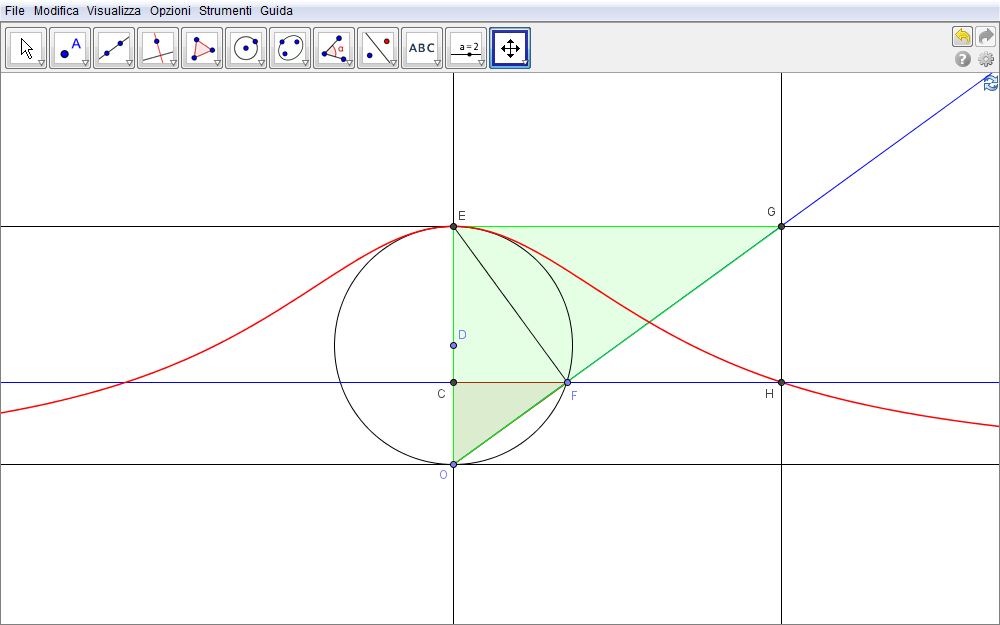
Figura 1.2. versiera02.ggb.
Per una definizione alternativa e di carattere geometrico evidenziamo i triangoli \(\triangle OFC\) e \(\triangle OGE\) (fig. 1.2). Questi sono evidentemente simili per cui vale la proporzione \begin{equation}{OC\over {CF}}={{OE}\over {EG}}.\end{equation} Poiché è pure \(EG=CH\) la precedente diviene \begin{equation}{OC\over {CF}}={{OE}\over {CH}}.\label{eq:defGeo}\end{equation} È in base a quest'ultima che si giustifica la definizione di versiera anche come il luogo dei punti H della generica retta CF perpendicolare al diametro OE per i quali vale la proporzione \eqref{eq:defGeo} (si veda pure in www.lorenzoroi.net/problemiesame.html il problema 1 dell'esame 2003 PNI e il problema 2/2013 Ordinamento).
Equazioni parametriche rappresentative
Per determinare le equazioni della versiera sia \(y=mx\) l'equazione del fascio di rette OF e, introdotto il parametro r > 0, l'equazione cartesiana della circonferenza c è \(c\colon x^2+(y-r)^2=r^2\). L'ascissa di G e quindi di H, discende dal sistema \begin{equation}G:\cases{y=2r\cr y=mx\cr}\quad\Rightarrow\quad 2r=mx\quad\Rightarrow\quad x={2r\over m},\end{equation} mentre l'ordinata di H deriva risolvendo il sistema \begin{equation}H:\cases{y=mx\cr x^2+(y-r)^2=r^2.\cr}\end{equation} Sostituiamo la \(x=y\,/m\) nella seconda equazione ottenendo \begin{equation}{y^2\over m^2}+y^2-2ry+r^2=r^2\quad\Rightarrow\quad y^2\biggl({1+m^2\over m^2}\biggr)-2ry=0.\end{equation} La precedente equazione ammette come soluzioni \(y=0\) e \begin{equation}y={2r\,m^2\over 1+m^2}.\end{equation} Pertanto le equazioni in termini del parametro m sono \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x={2r\over m}\cr\vphantom{x}\cr y={2r\,m^2\over 1+m^2}.\cr}\qquad m\not=0}\label{eq:param}\end{equation}
A ben vedere la parametrizzazione ottenuta con le equazioni \eqref{eq:param} non comprende un punto importante della versiera ossia il suo massimo \((0,2r)\). Difatti il fascio \(y=mx\) non può rappresentare la retta \(x=0\) che invece nella costruzione geometrica proposta appare del tutto accettabile. Tenendo conto di ciò ricordiamo il significato goniometrico del coefficiente angolare e cioè, se \(\theta\) è l'angolo tra l'asse x e la retta OF, \(m\) si può esprimere come \(m=\tan\theta\) (fig. 1.1). Ripresa inoltre l'identità \begin{equation}\sin^2\theta={\tan^2\theta\over 1+\tan^2\theta}={m^2\over 1+m^2}\end{equation} discende l'ulteriore rappresentazione parametrica \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x={2r\over \tan\theta}\cr\vphantom{x}\cr y=2r\sin^2\theta\cr}}\end{equation} che, ancora, non può comprendere \((0,2r)\). Se però riscriviamo il \((1/\tan\theta)\) come \((\cos\theta\,/\sin\theta)\) otteniamo \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x={2r \cos\theta\over \sin\theta}\cr\vphantom{x}\cr y=2r\sin^2\theta\cr}\qquad \theta\in]0,\pi[}\end{equation} che rappresenta pure il punto escluso dalle precedenti due parametrizzazioni. Infine se poniamo \(t=1/m\) e, indipendentemente dal suo legame con \(m\), consideriamo che \(t\) possa pure essere nullo, le equazioni \eqref{eq:param} diventano \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x={2r\over m}=2r t\cr\vphantom{x}\cr y={2r\over 1+{(1/m^2)}}={2r\over 1+t^2},\cr}}\label{eq:param2}\end{equation} forma razionale che rappresenta per intero la versiera.
Equazione cartesiana e funzione
In base alle \eqref{eq:param}, ma pure dalle \eqref{eq:param2}, è immediato dedurre l'equazione cartesiana che lega direttamente le coordinate di un punto della versiera. Difatti è sufficiente sostituire \(m=2r/x\) nella seconda per ottenere \begin{equation} y={2r\bigl({2r\over x}\bigr)^2\over 1+\bigl({2r\over x}\bigr)^2}={2r\cdot {4r^2\over x^2}\over 1+{4r^2\over x^2}}\end{equation} da cui \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{ y={8r^3\over 4r^2+x^2}}\label{eq:funz}\end{equation} o anche \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{4yr^2+y x^2=8r^3.}\label{eq:intera}\end{equation}
Quest'ultima equazione si può ottenere direttamente dalla \eqref{eq:defGeo} senza passare attraverso le precedenti rappresentazioni parametriche. Difatti con riferimento alla fig. 1.2 il secondo teorema di Euclide applicato a \(\triangle OFE\) fornisce \begin{equation}CF^2 = CO\cdot CE\quad\Rightarrow\quad CF=\sqrt{y(2r-y)}\end{equation} essendo \(y\) l'ordinata di F. Sostituendo tale risultato nella \eqref{eq:defGeo} abbiamo \begin{equation}{OC\over {CF}}={{OE}\over {CH}}\quad\Rightarrow\quad {y\over \sqrt{y(2r-y)}}={2r\over x}\end{equation} dalla quale con una quadratura (le grandezze coinvolte si sono implicitamente considerate positive) e una semplificazione si riottiene la \eqref{eq:intera}.
Circa la \eqref{eq:funz}, si veda anche quanto assegnato nel problema 2 dell'esame 2013 di ordinamento.
È comunque interessante notare come l'equazione \eqref{eq:funz} si possa interpretare come rappresentativa di una funzione di variabile reale avente per dominio l'insieme dei reali e dipendente dal parametro r. Per quanto mostrato dalla fig. 1.1, questa funzione è simmetrica rispetto all'asse y, possiede come asintoto orizzontale l'asse x e presenta un massimo assoluto in corrispondenza di \(x=0\) che vale \(y_{max}=2r\). Il suo codominio è quindi l'intervallo aperto a sinistra \(]0,2r]\).
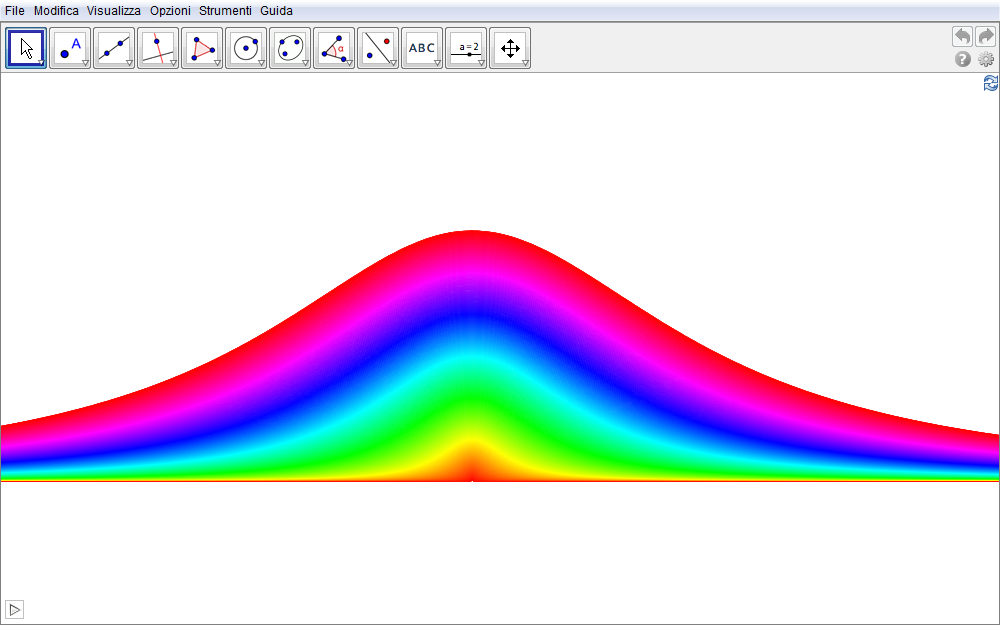
Nella figura sottostante un clic sull'icona in basso a sinistra avvia un'animazione dove, al variare del parametro r nell'intervallo \([0,5]\) e per incrementi di 0.02, viene rappresentata la corrispondente famiglia di curve.
Figura 1.3. versiera03.ggb.