In questa pagina esponiamo da un punto di vista elementare e in forma sintetica ma sostanzialmente completa le nozioni di base dell'algebra dei vettori. Lo scopo è di introdurre tale importante strumento concettuale e favorire un suo utilizzo anche nella risoluzione dei problemi geometrici ampliando la comune esperienza dello studio di tali nozioni fatta in ambito fisico. Trattiamo quindi della somma vettoriale, della scomposizione di un vettore e della sua rappresentazione cartesiana. Infine si riportano le definizioni e principali proprietà del prodotto scalare e vettoriale.
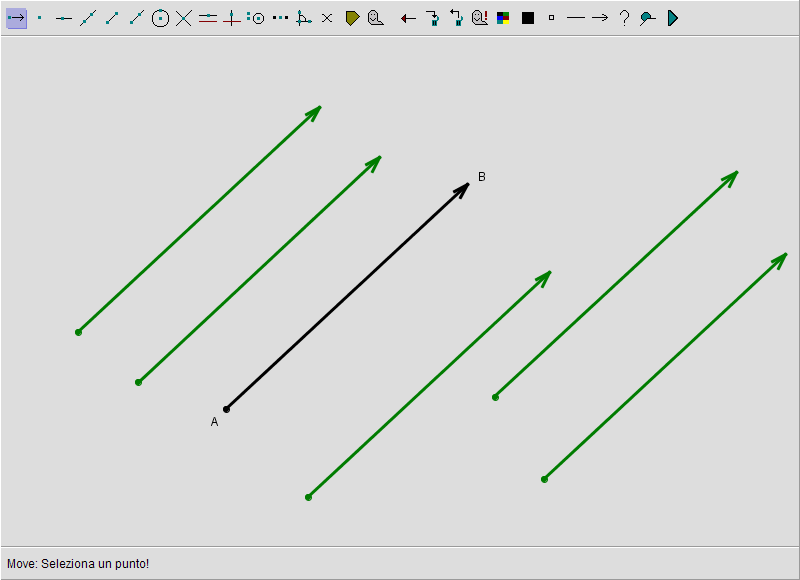
Per poter individuare univocamente la posizione di un punto B rispetto ad un altro A considerato come origine appare intuitivamente evidente come non sia sufficiente assegnare la sola misura della lunghezza del segmento AB ma, al contrario, si renda necessario fornire altre informazioni quali la direzione del segmento AB e il verso che, su questa direzione, collega il punto iniziale A con quello terminale B. Tutto questo contenuto informativo viene riassunto dal concetto di vettore, rappresentato in queste pagine dal simbolo di segmento riportato in neretto, ossia AB. La rappresentazione geometrica e grafica di tale vettore è data invece dall'insieme dei segmenti di retta aventi tutti la medesima direzione e verso e una lunghezza proporzionale alla parte scalare cioè alla misura della lunghezza del segmento AB. Tali segmenti si dicono segmenti orientati e, per l'appunto, se dotati della medesima direzione, verso e lunghezza si definiscono anche come segmenti equipollenti e rappresentano lo stesso vettore (in ambiti più formali si definisce sull'insieme dei segmenti orientati la relazione di equipollenza e le classi cui dà luogo si identificano con i vettori).
figura 1
In figura 1 riportiamo quindi alcuni segmenti orientati tutti rappresentativi del medesimo vettore AB in quanto caratterizzati dalla medesima direzione e verso così come dalla medesima lunghezza o, come si dice nel contesto dell'algebra dei vettori, modulo AB). (Nota. Abbiamo aggiunto tra le icone di Z.u.L. lo strumento vettore ![]() in modo da poter riportare graficamente un segmento come un vettore. Si tenga presente che tale strumento non interviene in alcuna costruzione e permette solo di modificare le apparenze di segmenti preesistenti: è in sostanza un elemento decorativo).
in modo da poter riportare graficamente un segmento come un vettore. Si tenga presente che tale strumento non interviene in alcuna costruzione e permette solo di modificare le apparenze di segmenti preesistenti: è in sostanza un elemento decorativo).
Introdotto (informalmente) il concetto di vettore è naturale definire delle operazioni che lo associno ad altri vettori o ad altre grandezze: qui iniziamo ricordando la definizione di somma vettoriale. Prendendo spunto da una situazione fisica consideriamo una particella che inizialmente si sposti da un punto A al punto B (fig. 2).
figura 2
Tale spostamento è rappresentato dal vettore a = AB. Successivamente la particella si muove da B a C e questo ulteriore spostamento viene rappresentato da b = BC. Lo spostamento complessivo è dato dal nuovo vettore c = AC. Quest'ultimo è quello che si definisce vettore somma di a e b. Difatti
Dalla definizione si deducono facilmente le seguenti proprietà:
In particolare dalla proprietà commutativa discende una definizione alternativa della somma (o risultante) di due vettori e conosciuta come la regola del parallelogramma. Questa consiste nell'individuare il vettore somma di due vettori non paralleli come il vettore rappresentato dalla diagonale del parallelogramma costruito per mezzo dei due vettori disposti in modo da avere l'origine in comune (in fig. 2 i segmenti orientati BC e AD rappresentano lo stesso vettore b).
Nel caso di tre o più vettori questa regola si estende facilmente considerando il poligono che si viene a formare connettendo l'origine di ogni vettore con l'estremo del precedente. Il vettore risultante si ottiene quindi unendo l'origine del primo con l'estremo dell'ultimo (fig. 3).
figura 3
Si definisce quindi il vettore opposto di a = AB come quel vettore che possiede la medesima direzione di a, modulo uguale ma verso opposto: esso è rappresentato dal segmento orientato BA e si pone –a = BA. In tal modo discende che a + (–a) = 0, dove 0 rappresenta il vettore nullo, rappresentato da segmenti orientati con gli estremi coincidenti e quindi dotato di modulo nullo e, convenzionalmente, di direzione e verso qualsiasi.
Diviene così possibile associare un significato alla differenza di vettori, simbolicamente data da a - b: questa verrà intesa come una somma tra il primo addendo e l'opposto del secondo d = a + (–b) (fig. 4). In tal modo, se la lunghezza della diagonale del parallelogramma costruito sui due vettori uscenti dallo stesso punto rappresenta il modulo del vettore somma, la seconda diagonale dello stesso parallelogramma fornisce la lunghezza del vettore differenza (fig. 4).
figura 4
Nel caso sia noto l'angolo α = ![]() CAB compreso tra due vettori (fig. 5) e, di questi, i rispettivi moduli |a| = AB e |b| = AC = BD,
CAB compreso tra due vettori (fig. 5) e, di questi, i rispettivi moduli |a| = AB e |b| = AC = BD,
il quadrato del modulo del vettore somma si ottiene sfruttando il teorema trigonometrico del coseno applicato a ![]() ABD. E dato che
ABD. E dato che ![]() ABD = 180° -
ABD = 180° - ![]() CAB ne segue
CAB ne segue
| |a + b|2 | = | AB2 | + | BD2 | - | 2 AB · BD cos( |
= | AB2 | + | BD2 | - | 2 AB · BD cos(180° - |
= | AB2 | + | AC2 | + | 2 AB · AC cos |
Nello stesso modo, il quadrato del modulo del vettore differenza risulta (fig. 5)
| |a - b|2 | = | AB2 | + | AC2 | - | 2 AB · AC cos( |
Dato uno scalare α rappresentativo di un numero reale e un vettore a è pure possibile definire una nuova operazione tale da associare a questi due un altro vettore. A tale scopo si dà la seguente definizione:
Si pone inoltre 1·a = a, 0·a = 0, –1·a = –a. Seguono direttamente dalla definizione le proprietà
Nelle successive figure 6 e 7 mostriamo come, al variare dello scalare α il vettore CD = αAB mantenga il proprio parallelismo con AB mentre il verso risulta concorde o discorde a seconda del segno di α (per variare α trascinare il punto P nelle due figure).
Dalla definizione di moltiplicazione scalare-vettore discende una condizione importante per stabilire se due vettori risultano paralleli o, come si suol dire nell'algebra dei vettori, collineari. Supposto non nullo il vettore a
Moltiplicando entrambi i membri di b = k a per un altro scalare non nullo β, si può esprimere questa condizione in una forma che si mostra più opportuna per successive generalizzazioni di tali nozioni. Difatti diviene
| β b | = | βk a | -βk a + β b = 0 | α a + β b = 0 | (1) |
dove si è posto - βk = α. Il termine α a + β b che costituisce il primo membro dell'ultima delle (1) si chiama una combinazione lineare dei vettori a e b. Questi ultimi sono collineari se quindi esiste una loro combinazione lineare nulla con coefficienti scalari (α e β) non contemporaneamente nulli. In tal caso, si dice pure che i due vettori sono linearmente dipendenti. In generale, due o più vettori a, b, c... si diranno invece linearmente indipendenti nel caso esista una loro combinazione lineare nulla
| α a | + | β b | + | γ b | + | ... | = | 0 | se e solo se | α = β = γ = ... = 0. |
Concludiamo questa sezione sottolineando che, date le definizioni e proprietà esposte finora e il fatto che le diagonali di un parallelogramma si bisecano vicendevolmente, la mediana AM di ![]() ABC (fig. 5) si può rappresentare in termini vettoriali come
ABC (fig. 5) si può rappresentare in termini vettoriali come
| AD | = | 2AM | = | AB + AC | ossia | AM | = | 1 2 |
(AB + AC). |
Questo fatto ci sarà utile nell'affrontare i problemi proposti di seguito.
Problema 12.1. Dimostrare che il segmento congiungente i punti medi dei due lati di ![]() ABC è parallelo al terzo lato ed è di lunghezza pari alla metà di questo.
ABC è parallelo al terzo lato ed è di lunghezza pari alla metà di questo.
Dimostrazione.
Problema 12.2. Dimostrare che la somma delle mediane in un triangolo è nulla.
Dimostrazione.
Problema 12.3. Determinare il punto X del piano cui appartiene ![]() ABC che soddisfa alla relazione vettoriale OX = OA + OB + OC essendo O il circocentro del triangolo.
ABC che soddisfa alla relazione vettoriale OX = OA + OB + OC essendo O il circocentro del triangolo.
Dimostrazione.
Problema 12.4. Detto O un punto qualsiasi del piano di ![]() ABC, dimostrare che il baricentro G di tale triangolo si esprime come
ABC, dimostrare che il baricentro G di tale triangolo si esprime come
| OG | = | 1 3 |
(OA + OB + OC). |
Problema 12.5. Dimostrare che il circocentro O, il baricentro G e l'ortocentro H di ![]() ABC sono allineati (vedere pure la pagina sulla linea di Eulero).
ABC sono allineati (vedere pure la pagina sulla linea di Eulero).
Dimostrazione.
Problema 12.6. Dimostrare che le diagonali di un quadrilatero si dividono scambievolmente a metà se e solo se il quadrilatero è un parallelogramma.
Dimostrazione.
Dato un vettore AB nel piano, scelte arbitrariamente due direzioni rappresentate da due rette non parallele in fig. 8, e proiettando gli estremi A e B su tali rette ossia condotte da questi estremi le parallele alle rette scelte, è possibile individuare due altri vettori tali che la loro somma dia il vettore di partenza.
figura 8
In simboli si ha
| AB | = | ABx | + | ABy |
e diremo che questa decomposizione, evidentemente non univoca data l'arbitrarietà nella scelta delle due rette, costrituisce una scomposizione del vettore AB. I vettori ABx e ABy si dicono i vettori componenti o proiezioni di AB sulle direzioni definite dalle due rette. Se poi associamo a ciascuna direzione un vettore, rispettivamente u e v (fig. 9) e notiamo la collinearità di u con ABx e di v con ABy allora per la condizione di collinearità è possibile determinare due scalari α e β tali che si possa scrivere
| ABx | = | α u | e | ABy | = | β v. |
figura 9
In definitiva la scomposizione di AB assume la forma
| AB | = | α u | + | β v | (2) |
che viene detta anche espansione di AB sulla base {u, v}.
Risulta particolarmente utile esprimere lo sviluppo (2) in termini di una base costituita da vettori di modulo unitario e mutuamente ortogonali. Detti quindi versori i vettori di modulo unitario, siano i e j due versori ortogonali. Nella base {i, j } il vettore AB possiede la scomposizione (fig. 10)
| AB | = | ax i | + | ay j |
dove gli scalari ax e ay saranno identificati come le componenti cartesiane del vettore.
figura 10
Le conseguenze di tali posizioni sono notevoli e conviene indagarle. Difatti definito tramite i versori {i, j } un sistema cartesiano (fig. 11. Utilizzare ![]() per evidenziarlo o toglierlo), sia OP un vettore di questo piano rappresentato da
per evidenziarlo o toglierlo), sia OP un vettore di questo piano rappresentato da
| OP | = | x i | + | y j. | (3) |
figura 11
È immediato notare che il vettore componente OA = x i possiede modulo OA = |x|·|i | = |x| e individua il punto dell'asse x rappresentato da A(x, 0). Analogamente per il vettore OB: la sua componente individua l'ordinata del punto B(0, y). Ne segue che la coppia (x, y) è, non solo rappresentativa delle componenti cartesiane del vettore OP ma pure fornisce le coordinate di P su tale piano cartesiano.
Più in generale siano A(xA, yA) e B(xB, yB) le coordinate cartesiane degli estremi del vettore AB. Vogliamo ottenere la scomposizione di AB nella base {i, j }. In riferimento alla figura 12 e osservato che OA + AB = OB, discende
figura 12
| AB | = | OB | - | OA | (4) |
D'altra parte, per quanto detto circa il vettore OP, i vettori OA e OB si potranno rappresentare come
| OA | = | xA i | + | yA j | OB | = | xB i | + | yB j. |
per cui introdotti in (4) e sfruttando le proprietà commutativa, associativa e distributiva, abbiamo
| AB | = | (xB i + yB j) - (xA i + yA j) |
| = | - xA i + xB i -yA j + yB j | |
| = | (xB - xA) i + (yB - yA) j |
Ciò giustifica la seguente importante conclusione:
|
Il modulo del vettore AB si deduce poi immediatamente applicando il teorema di Pitagora (fig. 12) ottenendo
| AB2 | = | (xB - xA)2 | + | (yB - yA)2 |
per cui, per i vettori in un piano, si ha
| | a |2 | = | ax2 | + | ay2 |
Sempre nel caso di vettori espressi tramite le rispettive componenti cartesiane
| a | = | ax i | + | ay j | b | = | bx i | + | by j, |
la somma e la moltiplicazione vettore-scalare si esprimono ora come
| a | + | b | = | (ax + bx) i | + | (ay + by) j | α a | = | (αax) i + (αay) j |
La fig. 13 ripropone graficamente la somma di due vettori e intende mettere in evidenza i legami esistenti tra i rispettivi vettori componenti cartesiani.
figura 13
Infine, quanto sopra, si estende naturalmente allo spazio tridimensionale. Per far ciò è sufficiente definire una terna di versori di base i, j, k ortogonali aventi la medesima origine (fig. 14). In tale sistema ciascuno di questi è individuato dalla terna di componenti (usiamo qui una notazione che evidenzia le sole componenti cartesiane e sottintende i versori della base)
e un vettore nello spazio possiede la decomposizione nei vettori componenti (fig. 14)
| a | = | ax i | + | ay j | + | az k | o, più sinteticamente, | a | = | (ax, ay, az) |
e che si dimostra essere unica in tale base.
figura 14
In termini delle coordinate A(xA, yA, zA), B(xB, yB, zB) degli estremi del vettore si ha inoltre
| ax | = | xB - xA | ay | = | yB - yA | az | = | zB - zA |
mentre il suo modulo risulta
| | a |2 | = | ax2 | + | ay2 | + | az2. |
Oltre alla somma e al prodotto scalare-vettore è possibile definire altre operazioni tra vettori. Una di queste è il prodotto scalare, operazione che associa a due vettori, uno scalare. La sua definizione, in termini delle componenti cartesiane dei due vettori a e b è la seguente:
| a | = | ax i | + | ay j | + | az k | b | = | bx i | + | by j | + | bz k |
|
È facile dimostrare che tale definizione assicura la validità della
Inoltre se b = a discende
| a.a | = | axax | + | ayay | + | azaz | = | ax2 | + | ay2 | + | az2 | = | a2 | = | | a |2 |
che fornisce il quadrato del modulo di a.
Una delle principali conseguenze di tale definizione consiste nel fatto che questo prodotto si annulla, non solo quando uno dei due vettori coincide con il vettore nullo ma pure quando questi sono mutuamente ortogonali. Lo si verifica facilmente eseguendo il prodotto scalare tra i versori i, j e k che sappiamo essere mutuamente perpendicolari. Difatti, tenendo conto della loro rappresentazione cartesiana, si ha
| i.j | = | 1·0 + 0·1 + 0·0 | = | 0 | i.k | = | 1·0 + 0·0 + 0·1 | = | 0 | j.k | = | 0·0 + 1·0 + 0·1 | = | 0 |
Più in generale, si può legare il prodotto scalare all'angolo formato dai due vettori fattori: vediamo come, analizzando alcuni casi particolari.
Consideriamo perciò due vettori del piano cartesiano, dei quali il primo abbia componente y nulla: siano quindi a = ax i e b = bx i + by j (fig. 15).
Calcolando il loro prodotto scalare si giunge alla a.b = axbx + 0by = axbx. Questo risultato mostra che il numero a.b sarà positivo quando ax e bx sono concordi, negativo se le due componenti sono discordi. Nel primo caso l'angolo tra i vettori (fig. 15) risulta acuto mentre nel secondo è ottuso. Se poi notiamo che |a x| = a cioè coincide con il modulo di a e bx con la proiezione di b lungo la direzione di a possiamo, almeno in questo caso, considerare il prodotto scalare equivalente al prodotto del modulo di a per la proiezione dell'altro nella direzione di a.
Questa conclusione particolare si può dimostrare in tutta generalità partendo dalla definizione data ma qui preferiamo mostrare come, dalla definizione alternativa seguente, discenda invece quella fornita inizialmente.
|
Per dimostrarne l'equivalenza riprendiamo l'espressione del quadrato del modulo della somma di due vettori ottenuta con l'applicazione del teorema del coseno e riportiamola in una forma più snella
| |a + b|2 | = | a2 + b2 + 2ab cos α |
con α angolo fra i vettori a e b. Da questa otteniamo che il termine ab cosα che compare nella definizione alternativa appena proposta si può riscrivere
| a.b | = | a b cos α | = | 1 2 |
(|a + b|2 - a2 - b2) | (5) |
Poiché il vettore a + b possiede componenti date dalla somma delle componenti dei singoli vettori coinvolti, il quadrato del suo modulo è
| |a + b|2 | = | (ax + bx)2 | + | (ay + by)2 | + | (az + bz)2 |
per cui sostituendo tale espressioni nella (5) otteniamo
| a.b | = | a b cos α | = | 1 2 |
(|a + b|2 - a2 - b2) |
| = | 1 2 |
[(ax + bx)2 + (ay + by)2 + (az + bz)2 - a2 - b2] | |||
| = | 1 2 |
[ax2 + bx2 + 2ax bx + ay2 + by2 + 2ay by + az2 + bz2 + 2az bz - a2 - b2] | |||
| = | 1 2 |
[(ax2 + ay2 + az2) + (bx2 + by2 + bz2) + 2ax bx + 2ay by + 2az bz - a2 - b2] |
Tenendo ancora conto delle espressioni del quadrato del modulo in termini delle componenti cartesiane
| a2 | = | ax2 | + | ay2 | + | az2 | b2 | = | bx2 | + | by2 | + | bz2 |
i primi due addendi entro parentesi quadre si elidono con gli ultimi due per cui giungiamo alla
| a.b | = |
|
||
| = | ax bx + ay by + az bz |
che è quanto si voleva dimostrare. Dato che i passaggi seguiti si possono eseguire nell'ordine inverso le due definizioni sono equivalenti e quindi potremo utilizzare indifferentemente l'una o l'altra delle definizioni. Quest'ultima comunque permette di evidenzare con maggior immediatezza alcune interessanti proprietà del prodotto scalare: dato che il prodotto bcosα si può interpretare come la componente (con segno) del vettore b nella direzione di a (fig. 16), possiamo affermare che qualsiasi sia la coppia dei vettori (del piano o dello spazio)
|
figura 16
Quest'ultimo risultato viene anche indicato come la condizione di perpendicolarità di due vettori.
Problema 12.7. In un ![]() ABC con AB = c, AC = b, BC = a, determinare la lunghezza della mediana AP.
ABC con AB = c, AC = b, BC = a, determinare la lunghezza della mediana AP.
Soluzione.
Problema 12.8. Dimostrare che la somma dei quadrati delle lunghezze delle diagonali di un parallelogramma è uguale alla somma dei quadrati delle lunghezze di tutti i suoi lati.
Dimostrazione.
Problema 12.9. Determinare l'area di ![]() ABC in termini delle lunghezze dei lati AB = c, AC = b, BC = a (formula di Erone).
ABC in termini delle lunghezze dei lati AB = c, AC = b, BC = a (formula di Erone).
Soluzione.
Problema 12.10. Determinare in termini dei vettori rappresentativi dei lati AB e AC il vettore che, con origine in A di ![]() ABC, individua un punto P del lato opposto che divide quest'ultimo in due parti tale che sia BP / PC = k.
ABC, individua un punto P del lato opposto che divide quest'ultimo in due parti tale che sia BP / PC = k.
Soluzione.
Problema 12.11. Utilizzando il risultato del problema precedente, esprimere la lunghezza delle bisettrici di un triangolo in termini dei suoi lati.
Soluzione.
Affrontiamo un'ultima operazione nell'insieme dei vettori, un'operazione che intendiamo come interna all'insieme dei vettori e tale da associare alla coppia di vettori a e b un vettore che simbolizzeremo come a x b. Questo vettore è definito come
| |a x b| | = | |a|·|b| senα | = | a b senα | = | abn | = | anb. |
Data tale definizione si intuisce che il prodotto vettoriale soddisfa alla proprietà anticommutativa
| a x b | = | - | b x a |
in quanto scambiando l'ordine dei fattori, il verso che porta il primo sul secondo risulta invertito mentre il modulo rimane invariato. Qualora si abbia
| a | = | ax i | + | ay j | + | az k | b | = | bx i | + | by j | + | bz k |
ossia i vettori siano espressi nella base { i, j, k }, lo sviluppo di a x b in termini delle componenti cartesiane dei vettori fattori non appare immediato cosicché conviene fornire direttamente la definizione che risulta essere
|
per cui le componenti di c sono
| cx | = | aybz | - | azby | cy | = | azbx | - | axbz | cz | = | axby | - | aybx |
e successivamente mostrare che questa soddisfa alle proprietà esposte inizialmente. Poiché l'espressione (6) risulta comunque difficile da memorizzare si ricorre ad una scrittura formale alternativa, detta determinante e del tipo
| c | = |
|
L'espressione esplicita di c si ottiene dalla precedente sviluppando il determinante (con le medesime regole dei determinanti che si incontrano nello studio dei sistemi lineari di equazioni) rispetto agli elementi della prima riga ossia rispetto ai versori della terna di base { i, j, k }. È quindi
|
|
|
dove il secondo determinante possiede coefficiente negativo in quanto relativo all'elemento j che presenta una somma (1 + 2 = 3) dispari degli indici di riga (prima) e colonna (seconda). Ciascun determinante di ordine due si calcola poi sommando il prodotto degli elementi della diagonale principale con l'opposto del prodotto degli elementi dell'altra diagonale.
Dimostriamo ora le principali proprietà geometriche della definizione (6) iniziando da quelle esposte inizialmente.
Ricordando che due vettori sono perpendicolari se il loro prodotto scalare è nullo, calcoliamo a.(a x b). Pertanto utilizzando le definizioni di prodotto scalare e vettoriale si ha
| a.(a x b) | = | ax(aybz - azby) - ay(axbz - azbx) +az(axby - aybx) |
| = | axaybz - axazby - ayaxbz + ayazbx + azaxby - azaybx | |
| = | 0 |
che conferma la perpendicolarità di a con a x b. Per la proprietà anticommutativa discende che
| b.(a x b) | = | - b.(b x a) | = - 0 = 0 |
per cui pure b![]() a x b.
a x b.
| |a x b| | = | |a|·|b| sen α, |
Questa proprietà si dimostra riscrivendo il quadrato dell'area in termini del coseno utilizzando l'identità sen2α = 1 - cos2α. Difatti poiché
| (ABDC)2 | = | (AB x CH)2 | = | (| a |·| b | senα)2 |
e sviluppato il quadrato, utilizziamo l'identità goniometrica ricordata
| (ABDC)2 | = | |a|2·|b|2 sen2α |
| = | |a|2·|b|2 (1-cos2α) | |
| = | |a|2·|b|2 - |a|2·|b|2 cos2α. |
In termini delle componenti cartesiane e in base alle definizioni (equivalenti) di prodotto scalare
| a.b | = | axbx + ayby + azbz | = | |a|·|b| cosα, |
l'espressione dell'area diventa
| (ABDC)2 | = | |a|2·|b|2 - |a|2·|b|2 cos2α | ||
| = | (ax2 + ay2 + az2)(bx2 + by2 + bz2) - (axbx + ayby + azbz)2 | |||
| = | ax2by2 + ax2bz2 + ay2bx2 + ay2bz2 + az2bx2 + az2by2 - 2axbxayby - 2axbxazbz - 2aybyazbz | (7) |
dove nell'ultimo passaggio si è eseguito il prodotto e sviluppato il quadrato. D'altra parte il modulo di a x b è dato anche da
| |a x b|2 | = | cx2 + cy2 + cz2 |
per cui, considerando esplicitamente le componenti discende per la (6)
| |a x b|2 | = | (aybz - azby)2 + (azbx - axbz)2 + (axby - aybx)2 |
Eseguendo i quadrati si giunge facilmente ad una espressione identica alla (7)
| |a x b|2 | = | ax2by2 + ax2bz2 + ay2bx2 + ay2bz2 + az2bx2 + az2by2 - 2axbxayby - 2axbxazbz - 2aybyazbz |
dimostrando l'asserto.
Se a è parallelo a b allora l'angolo α tra essi può assumere i valori α = 0° oppure α = 180°. In entrambi i casi il modulo di a x b si annulla essendo sen 0° = sen 180° = 0. Pertanto a x b = 0. In modo più formale, dall'ipotesi di collinearità tra a e b discende che b = β a essendo β un opportuno valore scalare per cui
| a x b | = | a x (β a) | = |
| = | (ayβ az - azβ ay) i + (azβ ax - axβ az) j + (axβ ay - ayβ ax) k |
e quest'ultima si può riscrivere
| a x b | = | β(ayaz - az ay) i + β(azax - axaz) j + β(axay - ayax) k | = | β 0 i + β 0 j + β 0 k | = 0. |
Viceversa, supponendo che a x b = 0 discende che le componenti cartesiane dovranno essere nulle ossia
| cx | = | aybz - azby = 0 | cy | = | azbx - axbz = 0 | cz | = | axby - aybx = 0 |
per cui
| aybz = azby | azbx = axbz | axby = aybx |
dalle quali deduciamo le uguaglianze tra rapporti
| bx ax |
= | by ay |
= | bz az |
Indicato con β il comune valore di questi rapporti, otteniamo
| bx = β ax | by = β ay | bz = β az |
che si possono riassumere nella b = β a. E quest'ultima stabilisce infine la collinearità cercata di a e b.
Allontanandoci dalle proprietà più marcatamente geometriche, affrontiamo la dimostrazione della già sottolineata proprietà anticommutativa.
Poiché dalla definizione discende
| b x a | = |
|
che esplicitamente risulta
| b x a | = | (byaz - bzay) i + (bzax - bxaz) j + (bxay - byax) k |
| = | - (- byaz + bzay) i - (- bzax + bxaz) j - (- bxay + byax) k |
e dove si è fattorizzato nel secondo passaggio un segno negativo. Appare ora evidente che con le proprietà distributiva e commutativa questa si può riscrivere in
| b x a | = | - (- byaz + bzay) i - (- bzax + bxaz) j - (- bxay + byax) k |
| = | - [(bzay - byaz) i + (bxaz - bzax) j + (byax - bxay) k] | |
| = | - [(aybz - azby) i + (azbx - axbz) j + (axby - aybx) k] |
Ma per la (6) l'ultima espressione risulta pari a -a x b e ciò completa la dimostrazione.
Concludiamo presentando pure le seguenti proprietà tutte facilmente dimostrabili per mezzo della rappresentazione cartesiana (6) del prodotto vettoriale.
Problema 12.12. Due triangoli ![]() ABC e
ABC e ![]() ACD sono situati nello stesso piano ed hanno in comune il lato AC. La retta AC divide inoltre il piano in due semipiani in modo che i punti B e D giacciono ciascuno in un diverso semipiano. Dimostrare che l'area del quadrilatero (ABCD) è pari a (ABCD) = 1/2 |AC x BD|.
ACD sono situati nello stesso piano ed hanno in comune il lato AC. La retta AC divide inoltre il piano in due semipiani in modo che i punti B e D giacciono ciascuno in un diverso semipiano. Dimostrare che l'area del quadrilatero (ABCD) è pari a (ABCD) = 1/2 |AC x BD|.
Soluzione.
Approfondimento 12.13. Discutere se sia possibile generalizzare la conclusione del problema precedente al caso in cui i vertici B e D appartengano al medesimo semipiano.
Discussione.
Problema 12.14. Dimostrare che (a x b)2 = a2 b2 - (a.b)2.
Soluzione.
|
|
||||||||||