ABC (figura 1). Pertanto siaNella pagina dimostriamo l'esistenza di un cerchio la cui circonferenza passa per ben nove punti caratteristici di un triangolo, se ne esplorano le proprietà e infine, si propongono alcuni problemi.
Riprendiamo la figura utilizzata per dimostrare l'esistenza della linea di Eulero e ai punti H, J e K, piedi delle altezze, P, Q e R punti medi dei lati ed estremi delle mediane, associamo una terza serie di punti ciascuno definito come il punto medio del segmento che ha per estremo un vertice, mentre l'altro estremo è l'ortocentro di ABC (figura 1). Pertanto sia
| AX = XO, | BY = YO, | CZ = ZO. |
figura 1
Notiamo che i due triangoli ABC e OBC hanno in comune il medesimo lato BC. Inoltre, fig. 2, i rimanenti due lati di ciascun triangolo vengono dimezzati rispettivamente da QR e YZ. Per il teorema dei punti medi, conseguenza del teorema di Talete segue che QR
YZ e che
| QR = YZ = | 1 2 |
BC |
figura 2
Passiamo ora a considerare i triangoli AOB e AOC (fig. 3).
figura 3
Questi hanno il lato AO in comune e, per la stessa ragione detta sopra, risulta RY QZ AO nonché
| RY = QZ = | 1 2 |
AO. |
In aggiunta va notato che AO è perpendicolare a BC in quanto parte dell'altezza AH per cui RY 
QR. Il parallelogramma QRYZ risulta essere quindi un rettangolo (fig. 4).
figura 4
Nello stesso modo si arriva a concludere che sono a loro volta rettangoli, i parallelogrammi RPZX e PQXY (figg. 5a, b).
figura 5a |
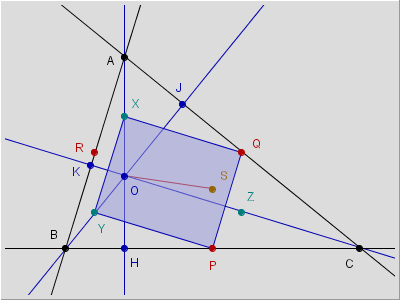
figura 5b |
Questi rettangoli condividono a coppie le stesse diagonali: difatti RZ è diagonale sia di QRYZ che di RPZX. Analogamente il rettangolo RPZX condivide con PQXY la diagonale XP. Pertanto, non solo possiedono diagonali congruenti ma pure il punto medio N di queste è il medesimo. Ciò significa che PX, QY e RZ sono tre diametri di un cerchio di centro N e perciò P, Z, Q, X, R, Y appartengono tutti alla medesima circonferenza (fig. 6).
figura 6
È infine facile dimostrare l'appartenenza a questa circonferenza dei piedi delle altezze: difatti essendo HPX rettangolo con ipotenusa PX che, come detto, è pure un diametro del precedente cerchio, ne segue l'appartenenza del punto H alla circonferenza di questo. Similmente per i punti J e K. Pertanto possiamo infine enunciare il
Il cerchio definito da questa circonferenza viene detto cerchio dei nove punti (o anche cerchio di Eulero o di Feuerbach). A dispetto dei molti nomi la prima dimostrazione della sua esistenza venne pubblicata da J. V. Poncelet nel 1821 mentre W. Feuerbach ottenne un'altra interessante proprietà di tale cerchio.
Ricordando quanto già osservato circa il rapporto esistente tra i raggi delle circonferenze circoscritte a ABC e, rispettivamente, PQR, ossia che PN = 1/2 AS = 1/2 rc possiamo affermare che il raggio del cerchio dei nove punti è la metà di quello circoscritto al triangolo. Inoltre poiché N risulta il circocentro di PQR e pure il punto medio della linea (segmento) di Eulero, possiamo enunciare che
Quest'ultimo teorema si può dimostrare in diversi modi: ne proponiamo altri due in aggiunta alla precedente deduzione.
Osservando la figura 7 appare immediato rilevare che i lati di XYZ sono paralleli ai lati di ABC e di lunghezza pari alla metà di questi ultimi. Ne segue che entrambi i triangoli condividono lo stesso ortocentro O. I punti X, Y e Z sono inoltre diametralmente opposti a P, Q, R per cui i due triangoli congruenti XYZ e PQR si ottengono uno dall'altro con una rotazione di 180° attorno al centro del cerchio. In tal modo vengono scambiati i rispettivi ortocentri dato che l'ortocentro di PQR è S. Ne segue che il centro del cerchio deve coincidere con il punto medio N di OS.
figura 7
In alternativa va notata la congruenza di NXO con NPS (fig. 8). Difatti valgono le congruenze tra gli angoli
NXO = NPS e XON = PSN
perché alterni interni di rette parallele.
figura 8
Essendo AO = 2 PS è anche OX = PS e, per il secondo criterio di congruenza si ha NXO
NPS: ne discende ON = NS (c.v.d.).
Aggiungiamo una seconda dimostrazione dell'esistenza del cerchio dei nove punti, in modo da evidenziare ulteriori legami esistenti tra gli elementi geometrici coinvolti.
figura 9
Innanzitutto consideriamo i triangoli HZY e OYZ (fig. 9). Questi sono congruenti in quanto possiedono un lato in comune YZ e gli angoli adiacenti congruenti (si tenga presente che, essendo Y e Z i punti medi delle ipotenuse di due triangoli rettangoli, BHO e COH, ciascuno di questi viene suddiviso in due triangoli isosceli). In particolare
YOZ = YHZ =180° - A
(per quest'ultima uguaglianza si veda la pagina sulla linea di Eulero).
figura 10
Poiché XYZ
ABC avendo i lati paralleli (e con rapporto 1:2), è anche YXZ =BAC. Ne segue che il quadrilatero HZXY avendo angoli opposti supplementari è inscrivibile in una circonferenza. Abbiamo quindi dimostrato l'appartenenza ad una medesima circonferenza dei punti X, Y, Z, H. Alla stessa circonferenza va aggiunto pure il punto P in quanto anche YPZ = 180° - A, essendo OYZPZY per quanto notato sul triangolo formato dai punti medi dei lati.
Ripetendo il ragionamento appena esposto anche per l'altezza BJ relativamente al lato CA, si giunge alla conclusione che anche i punti X, Y, Z, J, Q appartengono alla medesima circonferenza. Questa inoltre coincide con la precedente in quanto tra le due vi sono tre punti comuni (X, Y, Z) che definiscono un'unica circonferenza. Ad una simile conclusione si arriva trattando l'altezza CK e il lato AB e quindi possiamo concludere che tutti i punti X, Y, Z, H, P, Q, J, R, K, appartengono ad un'unica circonferenza (che coincide con quella circoscritta a XYZ).
figura 11
Vediamo di ottenere qualche altra proprietà del cerchio dei nove punti.
a) Innanzitutto, per quanto detto sopra è pure AX = PS per cui AXPS è un parallelogramma (figura 12).
b) Inoltre se osserviamo nella medesima figura i segmenti PX e JK, questi appaiono perpendicolari.
figura 12
Difatti PXAS e poiché ASJK per quanto dimostrato precedentemente (in quel caso il lato con estremi i piedi delle due altezze era descritto come QR), possiamo concludere che il diametro PX biseca la corda JK così come l'arco JK. Allo stesso modo Y è il punto medio dell'arco KH e Z biseca l'arco HJ.
c) Riprendiamo la figura relativa alle circonferenze ex-inscritte di un triangolo, mantenendo gli elementi essenziali (in particolare P, Q e R sono quindi i centri dei cerchi ex-inscritti) ed aggiungendo la circonferenza circoscritta a ABC (fig. 13).
figura 13
Poiché, per il teorema sulle bisettrici degli angoli formati da due rette vicendevolmente secanti, le bisettrici di ABC sono le altezze del triangolo PQR (formato dai centri delle circonferenze ex-inscritte), i vertici A, B e C sono a loro volta i piedi delle altezze di PQR. Ne segue che il cerchio circoscritto a ABC è il cerchio dei nove punti per PQR ossia per il triangolo che ha come vertici i centri delle tre circonferenze ex-inscritte.
Problema 3.1. Sia T il punto di intersezione della retta passante per l'ortocentro O di un triangolo e il punto medio (per esempio P in fig. 14) di un lato, con la circonferenza circoscritta e tale che il punto medio stia tra O e T. Dimostrare che il punto medio del lato è pure punto medio del segmento OT.
figura 14
Dimostrazione. Tracciati i segmenti CT e BT dimostriamo che BTCO è un parallelogramma. Difatti sappiamo che BOC = 180°-A (si veda quanto ne è seguito dalla discussione su un triangolo particolare). D'altra parte ABTC è un quadrilatero inscritto in un cerchio cosicché gli angoli opposti sono supplementari e risulta
BTC = 180° - CAB = 180° - A.
Il quadrilatero BTCO possiede pertanto una coppia di angoli opposti congruenti BOC = BTC. Poiché la diagonale OT passa per il punto medio dell'altra, BTCO è un parallelogramma.
Quanto affermato sopra possiede una interessante generalizzazione. Difatti
Verifica 3.1. Si consideri una retta per l'ortocentro O di un triangolo ABC. Dette U, U1 le sue intersezioni con la circonferenza dei nove punti e V, V1 quelle con la circonferenza circoscritta al triangolo, verificare che vale
| OU OV |
= | OU1 OV1 |
= | 1 2 |
qualsiasi sia la retta per O.
Verifica
Problema 3.1. Tre cerchi del medesimo raggio si intersecano in uno stesso punto P mentre a coppie si intersecano negli ulteriori punti A, B e C. Si dimostri che il cerchio circoscritto a ABC condivide il medesimo raggio dei tre e che P è l'ortocentro del triangolo.
Dimostrazione
Problema 3.2. Sia A1 l'intersezione dell'altezza relativa al lato BC con la circonferenza circoscritta a ABC. Dimostrare che la distanza dal centro del cerchio dei nove punti al lato BC è uguale a 1/4·AA1.
Dimostrazione
|
||||||||||
