Ritorna alla pagina di presentazione
Lorenzo Roi (novembre 2009)
Parte prima: obiettivi
La geometria differenziale studia con i metodi dell'analisi matematica le proprietà locali e globali di curve e superfici. Per far ciò ricerca innanzitutto quelle caratteristiche che siano indipendenti dalla particolare rappresentazione di una curva o di una superficie per cui, inizialmente, vengono precisati e definiti i concetti intuitivi di direzione e curvatura. Lo scopo di questo intervento è quello di proporre un percorso didattico che gradualmente conduca il lettore che disponga delle usuali nozioni della geometria analitica, del calcolo vettoriale, e dei concetti di derivata e di differenziale
Il testo, suddiviso in tre parti, discute nella prima (questa pagina) la rappresentazione parametrica della retta generalizzandola quindi ad una curva qualsiasi. Introduce quindi il vettore tangente per giungere infine a definire il versore tangente come una caratteristica locale di una opportuna classe di curve.
Nella seconda parte si chiarisce sulla base di esempi il concetto intuitivo di curvatura mentre nella terza lo si formalizza assieme alla definizione di centro di curvatura. Infine si esemplificano questi concetti applicandoli ad alcune curve.
Tutte le volte che si mostra utile una rappresentazione grafica della curva (e sono molte) o i calcoli da eseguire diventano tediosi ci appoggiamo alle capacità grafiche e simboliche del software Mathematica: nella versione prelevabile online di questo lavoro (sotto forma di notebook di Mathematica) saranno inoltre sfruttate le possibilità di animazione di tale programma con l'obiettivo di rendere lo studio più interattivo e intuitivamente più convincente. In tale versione è pure riportato il codice completo sia delle figure e sia delle deduzioni simboliche con in aggiunta qualche commento esplicativo sul codice adottato.
Rappresentazione parametrica della retta
Iniziamo con l'ottenere la rappresentazione parametrica di una retta che, evidentemente, possiamo ritenere la "curva" piu semplice. A tal fine utilizzeremo il concetto di vettori paralleli (o anche detti collineari), concetto che afferma il parallelismo di due vettori u e v se e solo se l'uno si può esprimere come la moltiplicazione di uno scalare t per l'altro ossia v=t u.
Siano quindi 
e 
due punti del piano cartesiano distinti. Per essi passa una sola retta r e inoltre definiscono il vettore 
. Un punto qualsiasi P(x, y) apparterrà ad r (fig. 1) se il vettore 
è parallelo o collineare a u ossia v=t u, relazione che si esplicita in termini delle componenti
o anche nel sistema
cioè
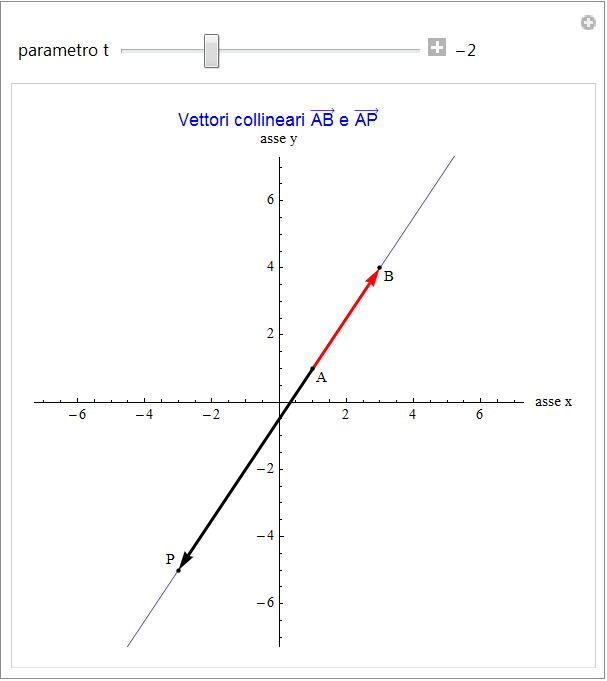
figura 1
Abbiamo in tal modo ottenuto la rappresentazione parametrica della retta passante per i due punti dati (fig. 1). Quest'ultima mostra una dipendenza lineare delle coordinate del punto P dal parametro reale t i cui coefficienti forniscono le componenti del vettore AB mentre i termini noti sono le coordinate di uno dei due punti (nell'esempio, di A). Viceversa, partendo dalla coppia di equazioni lineari
 | (1) |
associamo al punto P(x, y) il vettore OP avente l'estremo iniziale nell'origine O di un sistema cartesiano, al punto di coordinate A(a, b) il vettore OA = v = (a, b) e ai coefficienti di t il vettore u = (α, β). La coppia di equazioni (1) si può ora riscrivere come
da cui,
cioè ancora una relazione di collinearità tra il vettore costante u (che quindi individua una particolare direzione) e quello con estremo variabile OP - OA = OP + AO = AP (figura 2).
In definitiva la retta r si può esprimere tramite una funzione vettoriale lineare del parametro t del tipo
con u vettore che definisce la direzione e v che invece identifica un suo punto.
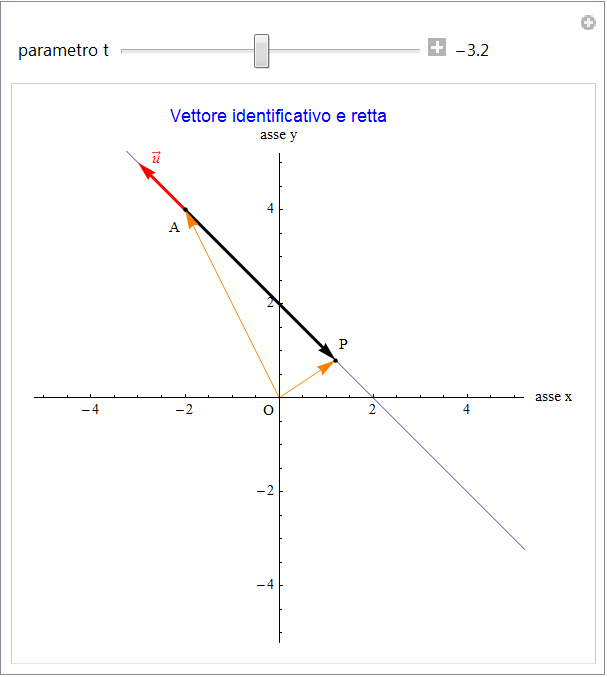
figura 2
Dato il vettore 
in termini delle componenti cartesiane, vogliamo associare ad esso un vettore perpendicolare. Per far ciò è sufficiente tener presente che due vettori non nulli sono perpendicolari se e solo se il loro prodotto scalare è nullo. Pertanto posto 
la condizione
sarà soddisfatta se, tra le varie possibilità, poniamo 
e 
. Il vettore 
risulta quindi perpendicolare ad u e, in particolare, si può facilmente verificare che si ottiene da quello iniziale con una rotazione antioraria di 90°. Per verificare ciò si può sperimentare con l'animazione seguente (fig. 3) dove si potranno variare le componenti del vettore u.
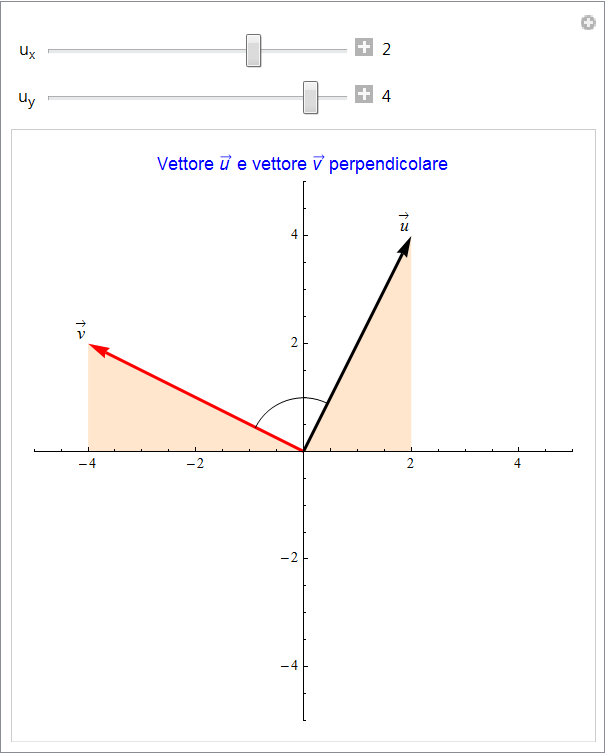
figura 3
Infine, se abbiamo una retta espressa dalle (1) caratterizzata dal vettore u = (α, β) e passante per A(a, b), la retta per A a essa perpendicolare (figura 4) sarà rappresentata dalle equazioni
 | (2) |
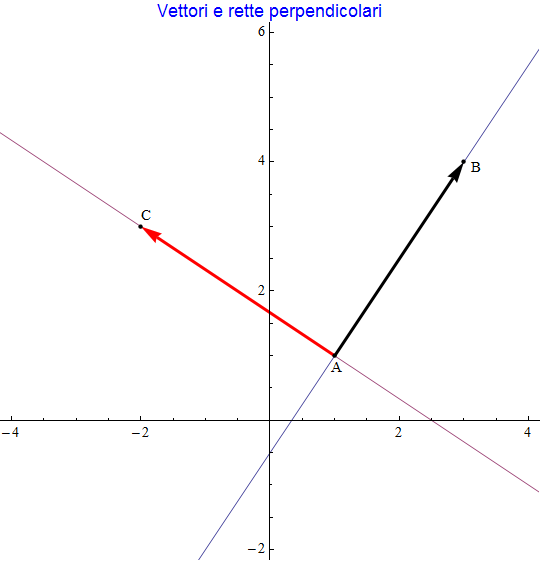
figura 4
Curve e vettore tangente
Nella sezione precedente abbiamo visto come le coordinate di un punto generico su una retta si possano rappresentare tramite due funzioni dipendenti linearmente da un parametro. Possiamo pure pensare (e le animazioni proposte confortano tale idea) la retta come un particolare luogo che viene percorso da un punto che si muove nel piano ossia, con termini mutuati dalla Fisica, come una particolare traiettoria seguita da un punto in moto. In tal caso il parametro rappresenterebbe la grandezza fisica tempo.
Queste osservazioni si possono naturalmente generalizzare per cui potremmo pensare di descrivere l'insieme di punti caratterizzanti una curva nel piano tramite una coppia di funzioni, entrambe dipendenti da un parametro e tali da rappresentare rispettivamente l'ascissa e l'ordinata di un punto in un sistema cartesiano: se al parametro associamo intuitivamente un istante temporale t, la curva che emerge si potrà considerare come la traiettoria seguita da un punto in moto.
Pertanto nel seguito considereremo assegnata una curva γ quando siano date le due funzioni
 | (3) |
dove t rappresenta un parametro reale variabile nell'insieme I (t ∈ I e I ⊆ R) e x e y le coordinate di un punto P(x, y) ∈ γ in un sistema cartesiano. Se O è l'origine del sistema cartesiano con assi definiti dai versori canonici i e j, la coppia di funzioni (3) si può pure interpretare come le componenti del vettore posizione del punto P, r = OP, nell'istante t ossia
Queste note costituiscono, in sostanza, la cosiddetta rappresentazione parametrica di una curva. Quale esempio, nella figura 5 viene rappresentata la curva espressa dalla coppia di funzioni 
e il vettore che identifica un suo punto generico (variabile nell'animazione associata alla figura).
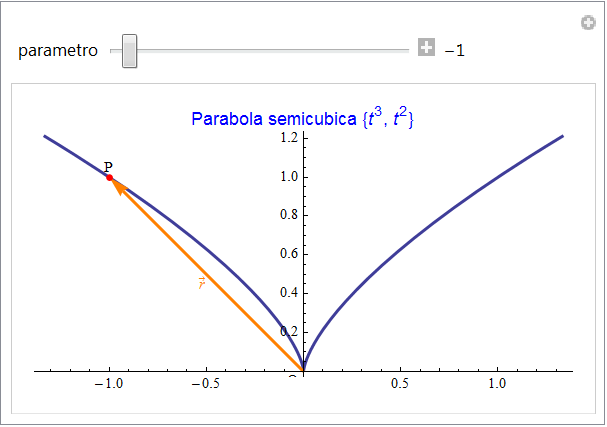
figura 5
In questa sezione vedremo come sia possibile assegnare a ogni punto di una (opportuna) curva espressa in forma parametrica il vettore tangente. La metodologia ricalca quella presente in tutti i manuali scolastici a riguardo del significato geometrico di derivata di una funzione data nella forma y = f(x) mentre qui se ne generalizza il risultato alla rappresentazione parametrica. Se quindi 
è un punto di una curva γ data dalle funzioni γ : {x(t), y(t)}, sia h un incremento del parametro t cui corrisponde su γ il punto 
. Possiamo ora associare a questi due punti il vettore 
avente per componenti
e se moltiplichiamo questo per lo scalare 1/h otteniamo un vettore 
ancora con la medesima direzione di 
Quest'ultimo caratterizza geometricamente la direzione della retta secante la curva γ e passante per i punti 
e P (nella figura 6, questo vettore è rappresentato in corrispondenza di un incremento h ≠ 0). Le componenti di tale vettore sono il rapporto incrementale di ciascuna funzione rappresentativa di γ: se, al tendere allo zero dell'incremento i limiti di questi rapporti incrementali esistono finiti, si pone
essendo 
e 
le derivate delle due funzioni di γ calcolate in 
. È noto che in tale processo la retta secante (e quindi pure il vettore s) tende ad assumere la direzione della retta tangente per cui si giustifica la definizione di vettore tangente t nel punto P(x(t), y(t)) come quel vettore le cui componenti siano espresse da
 | (4) |
Le animazioni seguenti (figg. 6 e 7) mostrano la situazione dal punto di vista geometrico: se h ≠ 0 appare il vettore secante s con in colore il triangolo delle sue componenti mentre se si pone h = 0 (che è la situazione iniziale) appare rappresentato il vettore tangente.
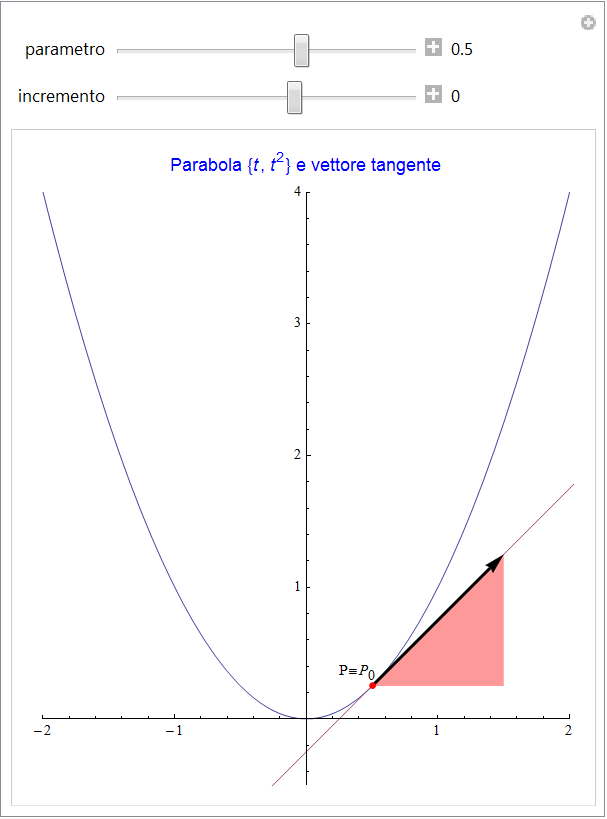
figura 6
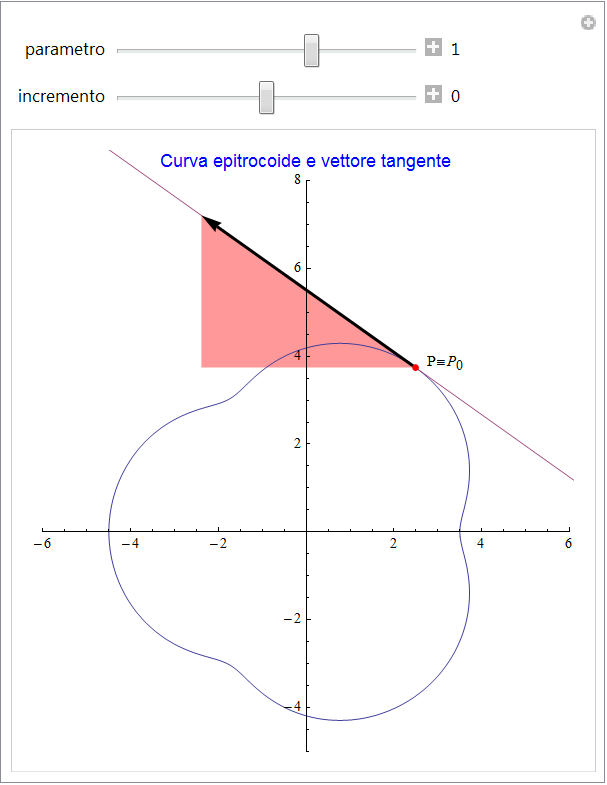
figura 7
In entrambe le figure 6 e 7 precedenti appare evidente come il vettore tangente vari da punto a punto sia in direzione che nel suo modulo. Volendo individuare caratteristiche intrinseche delle curve indipendenti dalla loro particolare rappresentazione, ci chiediamo se questa variabilità sia, appunto, una caratteristica intrinseca della curva o se dipenda dalla particolare parametrizzazione scelta. A tal fine riprendiamo la semplice parametrizzazione della parabola utilizzata nella figura 6, 
, e sostituiamo al parametro t il parametro - t cioè 
. Evidentemente la curva rimane la stessa (eliminando il parametro si giunge comunque all'equazione conosciuta 
) ma appare altrettanto evidente (figura 8) che tale trasformazione non fa altro che invertire il verso del vettore tangente: difatti si passa da t = (1, 2t) a t' = (-1, 2t) per cui per esempio, nel punto A(1, 1), corrispondente a t = 1 nella prima rappresentazione, il vettore tangente ha componenti 
mentre nella seconda rappresentazione dov'è t = -1 abbiamo che 
: i due vettori hanno, come aspettato, ancora la medesima direzione ma verso opposto.
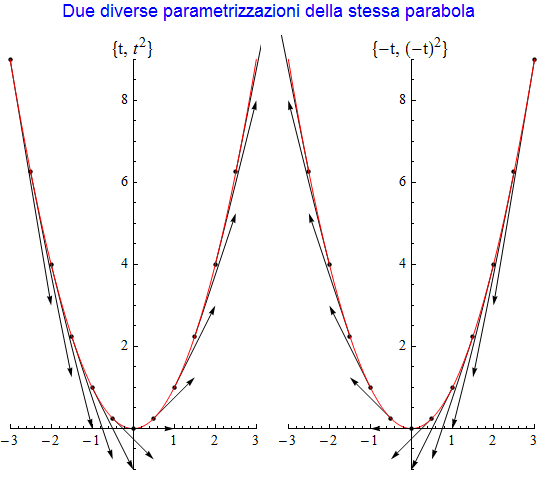
figura 8
Se consideriamo la curva in questione come la traiettoria di un punto in moto potremo dire che il vettore tangente dipende quindi dal verso di percorrenza del punto sulla curva. Tutto ciò appare naturale e coerente con la classica interpretazione fisica di una curva intesa come traiettoria di un corpo in moto e dove si associa al vettore tangente il vettore velocità (Nota: purtroppo questa interpretazione viene, di norma, proposta nei testi senza esplicitare i suoi stretti legami con la rappresentazione parametrica di funzioni). Passando ad una terza rappresentazione parametrica della medesima parabola data da 
discende immediatamente che il vettore tangente è dato da 
per cui cambia, in tal caso, pure il suo modulo. Difatti considerando sempre il medesimo punto A corrispondente questa volta a t = 1/2 risulta 
il cui modulo è diverso dal precedente pur mantenendo la medesima direzione. Un ulteriore esempio con una delle più semplici figure di Lissajous conferma ancora queste osservazioni (figura 9).
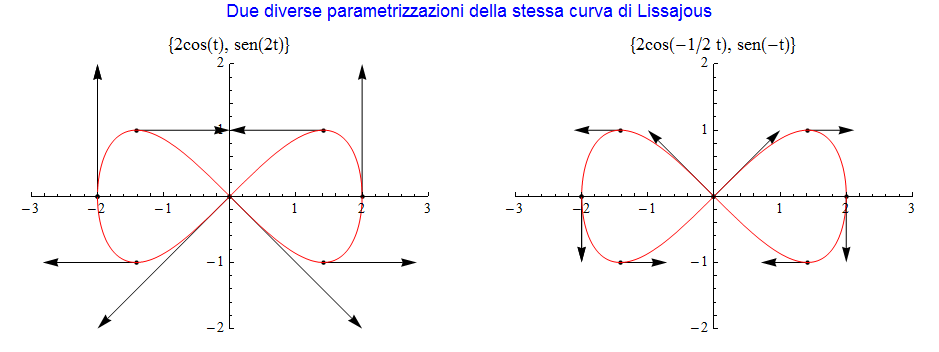
figura 9
Concludiamo sostenendo che l'unica caratteristica intrinseca della curva espressa dal vettore tangente è la sua direzione mentre modulo e verso dipendono dalla particolare parametrizzazione.
Siamo quindi giunti ad un primo importante risultato: da questo punto in poi sarà il versore tangente l'elemento che verrà associato a (quasi) ogni punto della curva in quanto, una volta che si sia scelto uno dei due possibili versi di percorrenza, esso è indipendente dalla rappresentazione scelta. Se quindi la curva γ è data dalle γ : {x(t), y(t)} il versore tangente associato localmente al punto corrispondente al valore t del parametro risulta
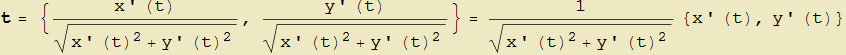 | (5) |
quest'ultimo ottenuto dividendo le componenti del vettore tangente espresso dalle (4) per il suo modulo (figura 10). Perché ciò sia possibile, devono essere evidentemente soddisfatte le condizioni
pertanto in quanto segue ci limiteremo a quelle curve che le rispettano, curve che per tale motivo vengono dette curve regolari.
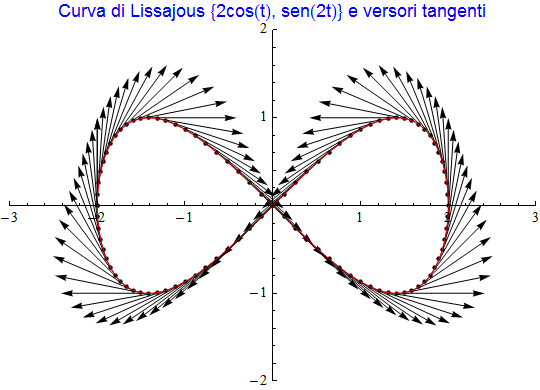
figura 10
L'ultima immagine (fig. 10) ci suggerisce di costruire ulteriori curve a partire da quelle date: difatti, siccome il versore tangente associa a un punto della curva data che è pure il suo estremo iniziale, un secondo punto che costituisce l'altra sua estremità, potremo studiare il luogo di questi ultimi punti. Se poi sostituiamo al versore tangente il versore normale
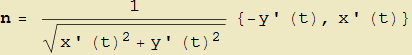 | (6) |
la curva descritta dall'estremo finale del versore normale (fig. 11) è invece un caso particolare di curva parallela ossia di curve che mantengono una distanza costante "d" dalla data curva. Così se moltiplichiamo tali versori per lo scalare d, il vettore che ne deriva avrà modulo pari a |d| e potremo visualizzare le curve che si ottengono al variare di tale parametro: l'animazione di fig. 12 permette appunto ciò a partire dalla curva di Lissajous precedente e con d = 1.
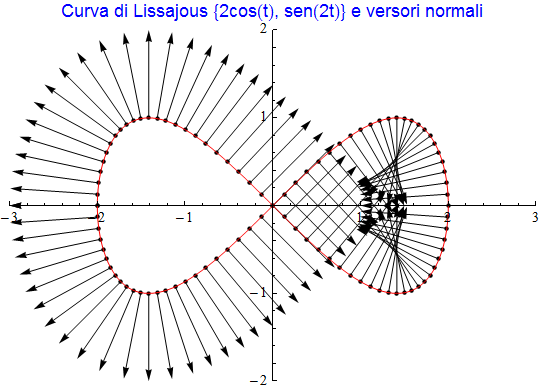
figura 11
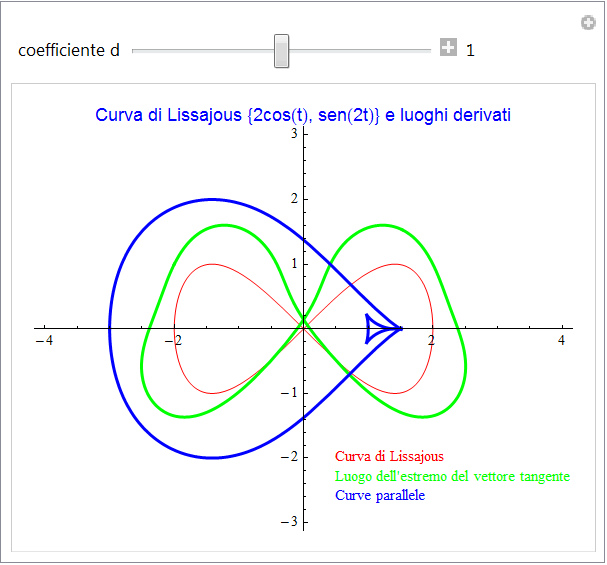
figura 12
Continua nella seconda parte.